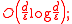Ε-net (computational geometry)
Encyclopedia
An ε-net is any of several related concepts in mathematics
, and in particular in computational geometry
, where it relates to the approximation of a general set by a collection of simpler subsets.
, and the elements of R are called ranges or hyperedges. An ε-net of a subset P of X is a subset N of P such that any range r ∈ R with |r ∩ P| ≥ ε|P| intersects N. In other words, any range that intersects at least a proportion ε of the elements of P must also intersect the ε-net N.
For example, suppose X is the set of points in the two-dimensional plane, R is the set of closed filled rectangles (products of closed intervals), and P is the unit square [0, 1] × [0, 1]. Then the set R consisting of the 8 points shown in the diagram to the right is a 1/4-net of P, because any closed filled rectangle intersecting at least 1/4 of the unit square must intersect one of these points. In fact, any (axis-parallel) square, regardless of size, will have a similar 8-point 1/4-net.
For any range space with finite VC dimension
d, regardless of the choice of P and ε, there exists an ε-net of P of size
because the size of this set is independent of P, any set P can be described using a set of fixed size.
This facilitates the development of efficient approximation algorithm
s. For example, suppose we wish to estimate an upper bound on the area of a given region P that falls inside a particular rectangle. One can estimate this to within an additive factor of ε times the area of P by first finding an ε-net of P, counting the proportion of elements in the ε-net falling inside the rectangle, and then multiplying by the area of P. The runtime of the algorithm depends only on ε and not P. One straightforward way to compute an ε-net with high probability is to take a sufficient number of random points, where the number of random points also depends only on ε. For example, in the diagram shown, any rectangle in the unit square containing at most three points in the 1/4-net has an area of at most 3/8 + 1/4 = 5/8.
ε-nets also provide approximation algorithms for the NP-complete
hitting set and set cover
problems.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, where it relates to the approximation of a general set by a collection of simpler subsets.
Background
Let X be a set and R be a set of subsets of X; such a pair is called a range space or hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
, and the elements of R are called ranges or hyperedges. An ε-net of a subset P of X is a subset N of P such that any range r ∈ R with |r ∩ P| ≥ ε|P| intersects N. In other words, any range that intersects at least a proportion ε of the elements of P must also intersect the ε-net N.
For example, suppose X is the set of points in the two-dimensional plane, R is the set of closed filled rectangles (products of closed intervals), and P is the unit square [0, 1] × [0, 1]. Then the set R consisting of the 8 points shown in the diagram to the right is a 1/4-net of P, because any closed filled rectangle intersecting at least 1/4 of the unit square must intersect one of these points. In fact, any (axis-parallel) square, regardless of size, will have a similar 8-point 1/4-net.
For any range space with finite VC dimension
VC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
d, regardless of the choice of P and ε, there exists an ε-net of P of size
because the size of this set is independent of P, any set P can be described using a set of fixed size.
This facilitates the development of efficient approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s. For example, suppose we wish to estimate an upper bound on the area of a given region P that falls inside a particular rectangle. One can estimate this to within an additive factor of ε times the area of P by first finding an ε-net of P, counting the proportion of elements in the ε-net falling inside the rectangle, and then multiplying by the area of P. The runtime of the algorithm depends only on ε and not P. One straightforward way to compute an ε-net with high probability is to take a sufficient number of random points, where the number of random points also depends only on ε. For example, in the diagram shown, any rectangle in the unit square containing at most three points in the 1/4-net has an area of at most 3/8 + 1/4 = 5/8.
ε-nets also provide approximation algorithms for the NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
hitting set and set cover
Set cover problem
The set covering problem is a classical question in computer science and complexity theory.It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms...
problems.