
230 (number)
Encyclopedia
230 is the natural number
following 229
and preceding 231.
, with its divisors being 2, 5, 10, 23, 46, and 115. Its factorisation makes it a sphenic number
. There is no integer with 230 coprime
s below it, thus 230 is a nontotient
. However, the sum of the coprime counts for the first 27 integers is 230.
There are 230 unique space group
s describing all possible crystal symmetries.
In base 10, being divisible by the sum of its digits, 230 is a Harshad number
.
, hexagonal number
, octahedral number
, Mertens function returns 0, and is the number of cubic inches in a U.S. liquid gallon
.
----
Two hundred [and] thirty-two 232 = 23·29, decagonal number, Mertens function returns 0, noncototient, refactorable number
----
Two hundred [and] thirty-three 233 prime, Fibonacci number
, Sophie Germain prime
, Chen prime
, Eisenstein prime
with no imaginary part, Markov number
, self number
, sum of 11 consecutive primes (5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41), teenage slang
for "best friends forever"
----
Two hundred [and] thirty-four 234 = 2·32·13, Harshad number
, nontotient
----
Two hundred [and] thirty-five 235 = 5·47, sum of three consecutive primes (73 + 79 + 83), Mertens function returns 0, Smarandache–Wellin number, centered triangular number
U-235
is the fissile
isotope
of uranium
used in the first atomic bombs.
----
Two hundred [and] thirty-six 236 = 22·59, Mertens function returns 0, nontotient, happy, sum of twelve consecutive primes (3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41)
----
Two hundred [and] thirty-seven 237 = 3·79, Blum integer
. Room 237 plays a significant role in the Stanley Kubrick
film "The Shining
"
----
Two hundred [and] thirty-eight 238 = 2·7·17, sphenic number
, sum of the first thirteen primes, Mertens function returns 0, untouchable number
.
----
Two hundred [and] thirty-nine
has its own article.
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
following 229
229 (number)
229 is the natural number between 228 and 230. It is also a prime number.The North American telephone area code 229 is assigned to the area around the city of Albany in southwestern Georgia in North America....
and preceding 231.
| Ordinal Ordinal number In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals... |
two hundred (and) thirty |
| Cardinal Cardinal number In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite... |
two hundred (and) thirtieth |
| Factorization Factorization In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original... | 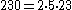 |
| Roman numeral | CCXXX |
| Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... |
11100110 |
| Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen... |
E6 |
In mathematics
It is a composite numberComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
, with its divisors being 2, 5, 10, 23, 46, and 115. Its factorisation makes it a sphenic number
Sphenic number
In number theory, a sphenic number is a positive integer which is the product of three distinct prime numbers.Note that this definition is more stringent than simply requiring the integer to have exactly three prime factors; e.g. 60 = 22 × 3 × 5 has exactly 3 prime factors, but is not sphenic.All...
. There is no integer with 230 coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
s below it, thus 230 is a nontotient
Nontotient
In number theory, a nontotient is a positive integer n which is not in the range of Euler's totient function φ, that is, for which φ = n has no solution. In other words, n is a nontotient if there is no integer x that has exactly n coprimes below it. All odd numbers are nontotients, except 1,...
. However, the sum of the coprime counts for the first 27 integers is 230.
There are 230 unique space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s describing all possible crystal symmetries.
In base 10, being divisible by the sum of its digits, 230 is a Harshad number
Harshad number
A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
.
In other fields
230 is:- A common voltageVoltageVoltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
in the European UnionEuropean UnionThe European Union is an economic and political union of 27 independent member states which are located primarily in Europe. The EU traces its origins from the European Coal and Steel Community and the European Economic Community , formed by six countries in 1958...
. - The year A.D. 230230Year 230 was a common year starting on Friday of the Julian calendar. At the time, it was known as the Year of the Consulship of Agricola and Clementinus...
or 230 BC230 BCYear 230 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Barbula and Pera...
. - +230 is the country code for Mauritius.
230 – 239
Two hundred [and] thirty-one 231 = 3·7·11, sphenic number, triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
, hexagonal number
Hexagonal number
A hexagonal number is a figurate number. The nth hexagonal number will be the number of points in a hexagon with n regularly spaced points on a side.The formula for the nth hexagonal number...
, octahedral number
Octahedral number
In number theory, an octahedral number is a figurate number that represents the number of spheres in an octahedron formed from close-packed spheres...
, Mertens function returns 0, and is the number of cubic inches in a U.S. liquid gallon
Gallon
The gallon is a measure of volume. Historically it has had many different definitions, but there are three definitions in current use: the imperial gallon which is used in the United Kingdom and semi-officially within Canada, the United States liquid gallon and the lesser used United States dry...
.
----
Two hundred [and] thirty-two 232 = 23·29, decagonal number, Mertens function returns 0, noncototient, refactorable number
----
Two hundred [and] thirty-three 233 prime, Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
, Sophie Germain prime
Sophie Germain prime
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
, Chen prime
Chen prime
A prime number p is called a Chen prime if p + 2 is either a prime or a product of two primes. The even number 2p + 2 therefore satisfies Chen's theorem....
, Eisenstein prime
Eisenstein prime
In mathematics, an Eisenstein prime is an Eisenstein integerz = a + b\,\omega\qquadthat is irreducible in the ring-theoretic sense: its only Eisenstein divisors are the units , a + bω itself and its associates.The associates and the complex conjugate...
with no imaginary part, Markov number
Markov number
A Markov number or Markoff number is a positive integer x, y or z that is part of a solution to the Markov Diophantine equationx^2 + y^2 + z^2 = 3xyz,\,studied by .The first few Markov numbers are...
, self number
Self number
A self number, Colombian number or Devlali number is an integer which, in a given base, cannot be generated by any other integer added to the sum of that other integer's digits. For example, 21 is not a self number, since it can be generated by the sum of 15 and the digits comprising 15, that is,...
, sum of 11 consecutive primes (5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41), teenage slang
Slang
Slang is the use of informal words and expressions that are not considered standard in the speaker's language or dialect but are considered more acceptable when used socially. Slang is often to be found in areas of the lexicon that refer to things considered taboo...
for "best friends forever"
----
Two hundred [and] thirty-four 234 = 2·32·13, Harshad number
Harshad number
A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
, nontotient
Nontotient
In number theory, a nontotient is a positive integer n which is not in the range of Euler's totient function φ, that is, for which φ = n has no solution. In other words, n is a nontotient if there is no integer x that has exactly n coprimes below it. All odd numbers are nontotients, except 1,...
----
Two hundred [and] thirty-five 235 = 5·47, sum of three consecutive primes (73 + 79 + 83), Mertens function returns 0, Smarandache–Wellin number, centered triangular number
Centered triangular number
A centered triangular number is a centered figurate number that represents a triangle with a dot in the center and all other dots surrounding the center in successive triangular layers...
U-235
Uranium-235
- References :* .* DOE Fundamentals handbook: Nuclear Physics and Reactor theory , .* A piece of U-235 the size of a grain of rice can produce energy equal to that contained in three tons of coal or fourteen barrels of oil. -External links:* * * one of the earliest articles on U-235 for the...
is the fissile
Fissile
In nuclear engineering, a fissile material is one that is capable of sustaining a chain reaction of nuclear fission. By definition, fissile materials can sustain a chain reaction with neutrons of any energy. The predominant neutron energy may be typified by either slow neutrons or fast neutrons...
isotope
Isotope
Isotopes are variants of atoms of a particular chemical element, which have differing numbers of neutrons. Atoms of a particular element by definition must contain the same number of protons but may have a distinct number of neutrons which differs from atom to atom, without changing the designation...
of uranium
Uranium
Uranium is a silvery-white metallic chemical element in the actinide series of the periodic table, with atomic number 92. It is assigned the chemical symbol U. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons...
used in the first atomic bombs.
----
Two hundred [and] thirty-six 236 = 22·59, Mertens function returns 0, nontotient, happy, sum of twelve consecutive primes (3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41)
----
Two hundred [and] thirty-seven 237 = 3·79, Blum integer
Blum integer
In mathematics, a natural number n is a Blum integer if n = p×q is a semiprime for which p and q are distinct prime numbers congruent to 3 mod 4. That is, p and q must be of the form 4t+3, for some integer t. Primes of this form are referred to as Blum primes. This means that the factors of a Blum...
. Room 237 plays a significant role in the Stanley Kubrick
Stanley Kubrick
Stanley Kubrick was an American film director, writer, producer, and photographer who lived in England during most of the last four decades of his career...
film "The Shining
The Shining (film)
The Shining is a 1980 psychological horror film produced and directed by Stanley Kubrick, co-written with novelist Diane Johnson, and starring Jack Nicholson, Shelley Duvall, and Danny Lloyd. The film is based on the novel of the same name by Stephen King. A writer, Jack Torrance, takes a job as an...
"
----
Two hundred [and] thirty-eight 238 = 2·7·17, sphenic number
Sphenic number
In number theory, a sphenic number is a positive integer which is the product of three distinct prime numbers.Note that this definition is more stringent than simply requiring the integer to have exactly three prime factors; e.g. 60 = 22 × 3 × 5 has exactly 3 prime factors, but is not sphenic.All...
, sum of the first thirteen primes, Mertens function returns 0, untouchable number
Untouchable number
An untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer ....
.
----
Two hundred [and] thirty-nine
239 (number)
239 is the natural number following 238 and preceding 240.-In mathematics:It is a prime number. The next is 241, with which it forms a pair of twin primes. 239 is a Sophie Germain prime and a Newman–Shanks–Williams prime...
has its own article.

