
Ascending chain condition on principal ideals
Encyclopedia
In abstract algebra
, the ascending chain condition
can be applied to the posets of principal left, principal right, or principal two-sided ideals of a ring
, partially ordered by inclusion
. The ascending ascending chain condition on principal ideals (abbreviated to ACCP) is satisfied if there is no infinite strictly ascending chain of principal ideal
s of the given type (left/right/two-sided) in the ring, or said another way, every ascending chain is eventually constant.
The counterpart descending chain condition may also be applied to these posets, however there is currently no need for the terminology "DCCP" since such rings are already called left or right perfect ring
s. (See Noncommutative ring section below.)
Noetherian ring
s (e.g. principal ideal domain
s) are typical examples, but some important non-Noetherian rings also satisfy (ACCP), notably unique factorization domain
s and left or right perfect rings.
. The proof of this relies on only (ACCP) not (ACC), so in any integral domain with (ACCP), an irreducible factorization exists. (In other words, any integral domains with (ACCP) are atomic
. But the converse is false, as shown in .) Such a factorization may not be unique; the usual way to establish uniqueness of factorizations uses Euclid's lemma
, which requires factors to be prime
rather that just irreducible. Indeed one has the following characterization: let A be an integral domain. Then the following are equivalent.
The so-called Nagata criterion holds for an integral domain A satisfying (ACCP): Let S be a multiplicatively closed subset of A generated by prime elements. If the localization
S−1A is a UFD, so is A. (Note that the converse of this is trivial.)
An integral domain A satisfies (ACCP) if and only if the polynomial ring A[t] does. The analogous fact is false if A is not an integral domain.
An integral domain where every finitely generated ideal is principal (that is, a Bézout domain
) satisfies (ACCP) if and only if it is a principal ideal domain
.
The ring Z+XQ[X] of all rational polynomials with integral constant term is an example of an integral domain (actually a GCD domain) that does not satisfy (ACCP), for the chain of principal ideals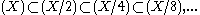
is non-terminating.
A theorem of Hyman Bass
in now known as "Bass' Theorem P" showed that the descending chain condition on principal left ideals of a ring R is equivalent to R being a right perfect ring
. D. Jonah showed in that there is a side-switching connection between the ACCP and perfect rings. It was shown that if R is right perfect (satisfies right DCCP), then R satisfies the left ACCP, and symmetrically, if R is left perfect (satisfies left DCCP), then it satisfies the right ACCP. The converses are not true, and the above switches from "left" and "right" are not typos.
Whether the ACCP holds on the right or left side of R, it implies that R has no infinite set of nonzero orthogonal idempotents, and that R is a Dedekind finite ring.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
can be applied to the posets of principal left, principal right, or principal two-sided ideals of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, partially ordered by inclusion
Inclusion
Inclusion may refer to:- Metallurgy :*Inclusion , a type of metal casting defect*Inclusions in Aluminium Alloys, solid particles in liquid aluminium alloy- Social inclusion of persons :...
. The ascending ascending chain condition on principal ideals (abbreviated to ACCP) is satisfied if there is no infinite strictly ascending chain of principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s of the given type (left/right/two-sided) in the ring, or said another way, every ascending chain is eventually constant.
The counterpart descending chain condition may also be applied to these posets, however there is currently no need for the terminology "DCCP" since such rings are already called left or right perfect ring
Perfect ring
In the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
s. (See Noncommutative ring section below.)
Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s (e.g. principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s) are typical examples, but some important non-Noetherian rings also satisfy (ACCP), notably unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s and left or right perfect rings.
Commutative rings
It is well known that a nonzero nonunit in a Noetherian integral domain factors into irreduciblesIrreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
. The proof of this relies on only (ACCP) not (ACC), so in any integral domain with (ACCP), an irreducible factorization exists. (In other words, any integral domains with (ACCP) are atomic
Atomic domain
In mathematics, more specifically ring theory, an atomic domain or factorization domain is an integral domain, every non-zero non-unit of which can be written as a product of irreducible elements...
. But the converse is false, as shown in .) Such a factorization may not be unique; the usual way to establish uniqueness of factorizations uses Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
, which requires factors to be prime
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
rather that just irreducible. Indeed one has the following characterization: let A be an integral domain. Then the following are equivalent.
- A is a UFD.
- A satisfies (ACCP) and every irreducible of A is prime.
- A is a GCD domainGCD domainIn mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
satisfying (ACCP).
The so-called Nagata criterion holds for an integral domain A satisfying (ACCP): Let S be a multiplicatively closed subset of A generated by prime elements. If the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
S−1A is a UFD, so is A. (Note that the converse of this is trivial.)
An integral domain A satisfies (ACCP) if and only if the polynomial ring A[t] does. The analogous fact is false if A is not an integral domain.
An integral domain where every finitely generated ideal is principal (that is, a Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
) satisfies (ACCP) if and only if it is a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
.
The ring Z+XQ[X] of all rational polynomials with integral constant term is an example of an integral domain (actually a GCD domain) that does not satisfy (ACCP), for the chain of principal ideals
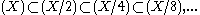
is non-terminating.
Noncommutative rings
In the noncommutative case, it becomes necessary to distinguish the right ACCP from left ACCP. The former only requires the poset of ideals of the form xR to satisfy the ascending chain condition, and the latter only examines the poset of ideals of the form Rx.A theorem of Hyman Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
in now known as "Bass' Theorem P" showed that the descending chain condition on principal left ideals of a ring R is equivalent to R being a right perfect ring
Perfect ring
In the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
. D. Jonah showed in that there is a side-switching connection between the ACCP and perfect rings. It was shown that if R is right perfect (satisfies right DCCP), then R satisfies the left ACCP, and symmetrically, if R is left perfect (satisfies left DCCP), then it satisfies the right ACCP. The converses are not true, and the above switches from "left" and "right" are not typos.
Whether the ACCP holds on the right or left side of R, it implies that R has no infinite set of nonzero orthogonal idempotents, and that R is a Dedekind finite ring.

