Augmented Lagrangian method
Encyclopedia
Augmented Lagrangian methods are a certain class of algorithm
s for solving constrained
optimization
problems. They have similarities to penalty method
s in that they replace a constrained optimization problem by a series of unconstrained problems; the difference is that the augmented Lagrangian method adds an additional term to the unconstrained objective. This additional term is
designed to mimic a Lagrange multiplier. The augmented Lagrangian is not the same as the method of Lagrange multipliers.
Viewed differently, the unconstrained objective is the Lagrangian of the constrained problem, with an additional penalty term (the augmentation).
The method was originally known as the method of multipliers, and was studied much in the 1970 and 1980s as a good alternative to penalty methods.
It was first discussed in Hestenes in 1969
and by Powell in 1969
The method was studied by R. Tyrrell Rockafellar
in relation to Fenchel duality, particularly in relation to proximal-point methods, Moreau–Yosida regularization, and maximal monotone operators: These methods were used in structural optimization
. The method was also studied and implemented by Dimitri Bertsekas
, notably in his 1982 book, and with respect to entropic regularization
(which accelerate the rate of convergence
for his "exponential method of multipliers").
Since the 1970s, sequential quadratic programming
(SQP) and interior point method
s (IPM) have had increasing attention, in part because they more easily use sparse matrix
subroutine
s from numerical
software libraries, and in part because IPMs have proven complexity results via the theory of self-concordant functions. The augmented Lagrangian method was rejuvenated by the optimization systems LANCELOT
and AMPL
, which allowed sparse matrix techniques to be used on seemingly dense but "partially separable" problems. The method is still useful for some problems. As of around 2007, there has been a resurgence of Augmented Lagrangian methods (and ADMM in particular) in fields such as total-variation denoising
and compressed sensing
; for example, the SALSA package was proposed in 2009.
A variant of the standard Augmented Lagrangian method that uses partial updates (similar to the Jacobi method
for solving linear equations) is known as the alternating direction method of multipliers or ADMM.
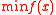
subject to
This problem can be solved as a series of unconstrained minimization problems. For reference, we first list the penalty method
approach:
The penalty method solves this problem, then at the next iteration it re-solves the problem
using a larger value of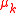
(and using the old solution as a the initial guess or "warm-start").
The augmented Lagrangian method uses the following unconstrained objective:
and after each iteration, in addition to updating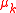
, the variable 
is also updated according to the rule
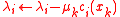
where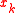
is the solution to the unconstrained problem at the kth step, i.e. 
The variable
is an estimate of the Lagrange multiplier, and the accuracy of this estimate improves at every step. The major advantage of the method is that unlike the penalty method
, it is not necessary to take
in order to solve the original constrained problem. Instead, because of the presence of the Lagrange multiplier term, 
can stay much smaller.
The method can be extended to handle inequality constraints. For a discussion of practical improvements, see .
since there is little extra computational cost and the parameter
need not go to infinity, thus avoiding ill-conditioning.
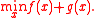
This is equivalent to the constrained problem
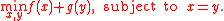
Though this change may seem trivial, the problem can now be attacked using methods of constrained optimization (in particular, the augmented Lagrangian method), and the objective function is separable in x and y. The dual update requires solving a proximity function in x and y at the same time; the ADMM technique allows this problem to be solved approximately by first solving for x with y fixed, and then solving for y with x fixed. Rather than iterate until convergence (like the Jacob method), the algorithm proceeds directly to updating the dual variable and then repeating the process. This is not equivalent to the exact minimization, but surprisingly, it can still be shown that this method converges to the right answer (under some assumptions). Because of this approximation, the algorithm is distinct from the pure augmented Lagrangian method.
The ADMM can be viewed as an application of the Douglas-Rachford splitting algorithm, and the Douglas-Rachford algorithm is in turn an instance of the Proximal point algorithm; details can be found here. There are several modern software packages that solve Basis pursuit and variants and use the ADMM; such packages include YALL1 (2009), SpaRSA (2009) and SALSA (2009).
and PENNON
.
The software MINOS
also uses an augmented Lagrangian method for some types of problems.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s for solving constrained
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problems. They have similarities to penalty method
Penalty method
Penalty methods are a certain class of algorithms for solving constrained optimization problems.A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem...
s in that they replace a constrained optimization problem by a series of unconstrained problems; the difference is that the augmented Lagrangian method adds an additional term to the unconstrained objective. This additional term is
designed to mimic a Lagrange multiplier. The augmented Lagrangian is not the same as the method of Lagrange multipliers.
Viewed differently, the unconstrained objective is the Lagrangian of the constrained problem, with an additional penalty term (the augmentation).
The method was originally known as the method of multipliers, and was studied much in the 1970 and 1980s as a good alternative to penalty methods.
It was first discussed in Hestenes in 1969
and by Powell in 1969
The method was studied by R. Tyrrell Rockafellar
R. Tyrrell Rockafellar
* for the George Dantzig Prize in 1994 in Optima, Issue 44 page 5.- Books :* Rockafellar, R. Tyrrell. Conjugate duality and optimization. Lectures given at the Johns Hopkins University, Baltimore, Md., June, 1973. Conference Board of the Mathematical Sciences Regional Conference Series in Applied...
in relation to Fenchel duality, particularly in relation to proximal-point methods, Moreau–Yosida regularization, and maximal monotone operators: These methods were used in structural optimization
Structural engineering
Structural engineering is a field of engineering dealing with the analysis and design of structures that support or resist loads. Structural engineering is usually considered a specialty within civil engineering, but it can also be studied in its own right....
. The method was also studied and implemented by Dimitri Bertsekas
Dimitri Bertsekas
Dimitri Bertsekas is an applied mathematician and computer scientist, and a professor at the department of Electrical Engineering and Computer Science at the Massachusetts Institute of Technology , Cambridge, Massachusetts.- Biography :...
, notably in his 1982 book, and with respect to entropic regularization
Bregman divergence
In mathematics, the Bregman divergence or Bregman distance is similar to a metric, but does not satisfy the triangle inequality nor symmetry. There are two ways in which Bregman divergences are important. Firstly, they generalize squared Euclidean distance to a class of distances that all share...
(which accelerate the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
for his "exponential method of multipliers").
Since the 1970s, sequential quadratic programming
Sequential quadratic programming
Sequential quadratic programming is an iterative method for nonlinear optimization. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable....
(SQP) and interior point method
Interior point method
Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
s (IPM) have had increasing attention, in part because they more easily use sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
subroutine
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
s from numerical
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
software libraries, and in part because IPMs have proven complexity results via the theory of self-concordant functions. The augmented Lagrangian method was rejuvenated by the optimization systems LANCELOT
Galahad library
The Galahad library is a thread-safe library of packages for the solution of optimization—or mathematical programming—problems. The areas covered by the library are unconstrained and bound-constrained optimization, quadratic programming, nonlinear programming, systems of nonlinear equations and...
and AMPL
AMPL
AMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and solving high-complexity problems for large-scale mathematical computation AMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and...
, which allowed sparse matrix techniques to be used on seemingly dense but "partially separable" problems. The method is still useful for some problems. As of around 2007, there has been a resurgence of Augmented Lagrangian methods (and ADMM in particular) in fields such as total-variation denoising
Total variation denoising
In signal processing, Total variation denoising, also known as total variation regularization is a process, most often used in digital image processing that has applications in noise removal. It is based on the principle that signals with excessive and possibly spurious detail have high total...
and compressed sensing
Compressed sensing
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
; for example, the SALSA package was proposed in 2009.
A variant of the standard Augmented Lagrangian method that uses partial updates (similar to the Jacobi method
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
for solving linear equations) is known as the alternating direction method of multipliers or ADMM.
General method
Let us say we are solving the following constrained problem: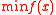subject to
This problem can be solved as a series of unconstrained minimization problems. For reference, we first list the penalty method
Penalty method
Penalty methods are a certain class of algorithms for solving constrained optimization problems.A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem...
approach:
The penalty method solves this problem, then at the next iteration it re-solves the problem
using a larger value of
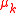(and using the old solution as a the initial guess or "warm-start").The augmented Lagrangian method uses the following unconstrained objective:
and after each iteration, in addition to updating
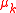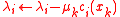
, the variable is also updated according to the rulewhere
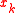is the solution to the unconstrained problem at the kth step, i.e. The variable
is an estimate of the Lagrange multiplier, and the accuracy of this estimate improves at every step. The major advantage of the method is that unlike the penalty methodPenalty method
Penalty methods are a certain class of algorithms for solving constrained optimization problems.A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem...
, it is not necessary to take
in order to solve the original constrained problem. Instead, because of the presence of the Lagrange multiplier term, can stay much smaller.The method can be extended to handle inequality constraints. For a discussion of practical improvements, see .
Comparison with penalty methods
From , it is suggested that the augmented Lagrangian method is generally preferred to the quadratic penalty methodsince there is little extra computational cost and the parameter
need not go to infinity, thus avoiding ill-conditioning.Alternating direction method of multipliers
The alternating direction method of multipliers (ADMM) is a variant of the augmented Lagrangian scheme that uses partial updates for the dual variables. This method is often applied to solve problems such as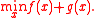This is equivalent to the constrained problem
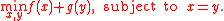
Though this change may seem trivial, the problem can now be attacked using methods of constrained optimization (in particular, the augmented Lagrangian method), and the objective function is separable in x and y. The dual update requires solving a proximity function in x and y at the same time; the ADMM technique allows this problem to be solved approximately by first solving for x with y fixed, and then solving for y with x fixed. Rather than iterate until convergence (like the Jacob method), the algorithm proceeds directly to updating the dual variable and then repeating the process. This is not equivalent to the exact minimization, but surprisingly, it can still be shown that this method converges to the right answer (under some assumptions). Because of this approximation, the algorithm is distinct from the pure augmented Lagrangian method.
The ADMM can be viewed as an application of the Douglas-Rachford splitting algorithm, and the Douglas-Rachford algorithm is in turn an instance of the Proximal point algorithm; details can be found here. There are several modern software packages that solve Basis pursuit and variants and use the ADMM; such packages include YALL1 (2009), SpaRSA (2009) and SALSA (2009).
Software
Some well-known software packages that use the augmented Lagrangian method are LANCELOTGalahad library
The Galahad library is a thread-safe library of packages for the solution of optimization—or mathematical programming—problems. The areas covered by the library are unconstrained and bound-constrained optimization, quadratic programming, nonlinear programming, systems of nonlinear equations and...
and PENNON
PENOPT
PENOPT is an optimization software package. Its goal is to develop a unified approach to problems of nonlinear programming and semidefinite programming. The solvers are based on a generalized augmented Lagrangian method combined with the Trust region algorithm.The software was developed by Michal...
.
The software MINOS
MINOS (optimization software)
MINOS is a linear and nonlinear mathematical optimization solver that runs with TOMLAB, GAMS, AMPL and AIMMS and a range of other mathematical modelling packages. For linear problems the software employs a simplex method, while for nonlinear problems a reduced-gradient method is used...
also uses an augmented Lagrangian method for some types of problems.
See also
- Penalty methodPenalty methodPenalty methods are a certain class of algorithms for solving constrained optimization problems.A penalty method replaces a constrained optimization problem by a series of unconstrained problems whose solutions ideally converge to the solution of the original constrained problem...
s - Barrier method
- Barrier functionBarrier functionIn constrained optimization, a field of mathematics, a barrier function is a continuous function whose value on a point increases to infinity as the point approaches the boundary of the feasible region . It is used as a penalizing term for violations of constraints...
- Lagrange multiplier