Bargaining Problem
Encyclopedia
The two person bargaining problem is a problem of understanding how two agents should cooperate when non-cooperation leads to Pareto-inefficient
results. It is in essence an equilibrium selection problem; Many games have multiple equilibria with varying payoffs for each player, forcing the players to negotiate on which equilibrium to target. The quintessential example of such a game is the Ultimatum game
. The underlying assumption of bargaining theory is that the resulting solution should be the same solution an impartial arbitrator would recommend. Solutions to bargaining come in two flavors: an axiomatic approach where desired properties of a solution are satisfied and a strategic approach where the bargaining procedure is modeled in detail as a sequential game.
used to model bargaining interactions. In the Nash Bargaining Game two players demand a portion of some good (usually some amount of money). If the total amount requested by the players is less than that available, both players get their request. If their total request is greater than that available, neither player gets their request. A Nash bargaining solution is a (Pareto efficient
) solution to a Nash bargaining game.
According to Walker (2005), Nash's bargaining solution was shown by John Harsanyi
to be the same as Zeuthen
's solution of the bargaining problem (Problems of Monopoly and Economic Warfare, 1930).
The Battle of the Sexes
, as shown, is a two player coordination game
. Both Opera/Opera and Football/Football are Nash equilibria. Any probability distribution over these two Nash equilibria is a correlated equilibrium
. The question then becomes which of the infinitely many possible equilibria should be chosen by the two players. If they disagree and choose different distributions, they are likely receive 0 payoffs. In this symmetric case the natural choice is to play Opera/Opera and Football/Football with equal probability. Indeed all bargaining solutions described below prescribe this solution. However, if the game is asymmetric --- for example, Football/Football instead yields payoffs of 2,5 --- the appropriate distribution is less clear. The problem of finding such a distribution is addressed by the bargaining theory.
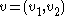, where 
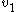and 
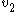are the respective payoffs to players 1 and player 2, and a feasibility set 
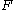, a closed convex subset of 
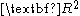, the elements of which are interpreted as agreements. Set 
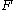is convex because an agreement could take the form of a correlated combination of other agreements. The problem is nontrivial if agreements in 
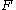are better for both parties than the disagreement. The goal of bargaining is to choose the feasible agreement 
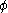in 
that could result from negotiations.
is the value the players can expect to receive if negotiations break down. This could be some focal equilibrium that both players could expect to play. This point directly affects the bargaining solution, however, so it stands to reason that each player should attempt to choose his disagreement point in order to maximize his bargaining position. Towards this objective, it is often advantageous to increase one's own disagreement payoff while harming the opponent's disagreement payoff (hence the intrepretation of the disagtreement as a threat). If threats are viewed as actions, then one can construct a separate game wherein each player chooses a threat and receives a payoff according to the outcome of bargaining. It is known as Nash's variable threat game. Alternatively, each player could play a minimax
strategy in case of disagreement, choosing to disregard personal reward in order to hurt the opponent as much as possible shoud the opponent leave the bargaining table.
[d, z], where z is the total good. If x + y is equal to or less than z, the first player receives x and the second y. Otherwise both get d. d here represents the disagreement point or the threat of the game; often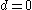
.
There are many Nash equilibria in the Nash bargaining game. Any x and y such that x + y = z is a Nash equilibrium. If either player increases their demand, both players receive nothing. If either reduces their demand they will receive less than if they had demanded x or y. There is also a Nash equilibrium where both players demand the entire good. Here both players receive nothing, but neither player can increase their return by unilaterally changing their strategy.
Let u and v be the utility functions of Player 1 and Player 2, respectively. In the Nash bargaining solution, the players will seek to maximize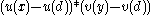
, where 
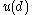and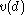 
, are the status quo
utilities (i.e. the utility obtained if one decides not to bargain with the other player). The product of the two excess utilities is generally referred to as the Nash product.
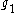with player 2’s help (and vice-versa for 
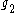), then the Kalai-Smorodinsky bargaining solution would yield the point 
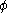on the Pareto frontier such that 
.
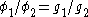, and the axiom of monotonicity. It is the solution which attempts to grant equal gain to both parties. In other words, it is the point which maximizes the minimum payoff among players.
and economists
have recently used the Nash bargaining game to explain the emergence of human attitudes toward distributive justice
(Alexander 2000; Alexander and Skyrms 1999; Binmore 1998, 2005). These authors primarily use evolutionary game theory
to explain how individuals come to believe that proposing a 50-50 split is the only just
solution to the Nash Bargaining Game.
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
results. It is in essence an equilibrium selection problem; Many games have multiple equilibria with varying payoffs for each player, forcing the players to negotiate on which equilibrium to target. The quintessential example of such a game is the Ultimatum game
Ultimatum game
The ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. ...
. The underlying assumption of bargaining theory is that the resulting solution should be the same solution an impartial arbitrator would recommend. Solutions to bargaining come in two flavors: an axiomatic approach where desired properties of a solution are satisfied and a strategic approach where the bargaining procedure is modeled in detail as a sequential game.
The bargaining game
The bargaining game or Nash bargaining game is a simple two-player gameGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
used to model bargaining interactions. In the Nash Bargaining Game two players demand a portion of some good (usually some amount of money). If the total amount requested by the players is less than that available, both players get their request. If their total request is greater than that available, neither player gets their request. A Nash bargaining solution is a (Pareto efficient
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
) solution to a Nash bargaining game.
According to Walker (2005), Nash's bargaining solution was shown by John Harsanyi
John Harsanyi
John Charles Harsanyi was a Hungarian-Australian-American economist and Nobel Memorial Prize in Economic Sciences winner....
to be the same as Zeuthen
Zeuthen Strategy
The Zeuthen strategy is a negotiation strategy used by some artificial agents. Its purpose is to measure the willingness to risk conflict. An agent will be more willing to risk conflict if the difference in utility between its current proposal and the conflict deal is low.When used by both agents...
's solution of the bargaining problem (Problems of Monopoly and Economic Warfare, 1930).
An example
The Battle of the Sexes
Battle of the sexes
-Films:*The Battle of the Sexes , American film directed by D. W. Griffith*The Battle of the Sexes , American remake of the above, also directed by D. W. Griffith...
, as shown, is a two player coordination game
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
. Both Opera/Opera and Football/Football are Nash equilibria. Any probability distribution over these two Nash equilibria is a correlated equilibrium
Correlated equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann . The idea is that each player chooses his/her action according to his/her observation of the value of the same public...
. The question then becomes which of the infinitely many possible equilibria should be chosen by the two players. If they disagree and choose different distributions, they are likely receive 0 payoffs. In this symmetric case the natural choice is to play Opera/Opera and Football/Football with equal probability. Indeed all bargaining solutions described below prescribe this solution. However, if the game is asymmetric --- for example, Football/Football instead yields payoffs of 2,5 --- the appropriate distribution is less clear. The problem of finding such a distribution is addressed by the bargaining theory.
Formal description
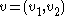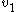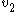A two person bargain problem consists of a disagreement, or threat, point, where and are the respective payoffs to players 1 and player 2, and a feasibility set 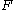, a closed convex subset of 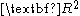, the elements of which are interpreted as agreements. Set 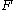is convex because an agreement could take the form of a correlated combination of other agreements. The problem is nontrivial if agreements in 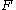are better for both parties than the disagreement. The goal of bargaining is to choose the feasible agreement 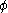in that could result from negotiations.Feasibility set
Which agreements are feasible depends on whether barganing is mediated by an additional party. When binding contracts are allowed, any joint action is playable, and the feasibility set consists of all attainable payoffs better than the disagreement point. When binding contracts are unavailable, the players can defect (moral hazard), and the feasibility set is composed of correlated equilibria, since these outcomes require no exogenous enforcement.Disagreement point
The disagreement point is the value the players can expect to receive if negotiations break down. This could be some focal equilibrium that both players could expect to play. This point directly affects the bargaining solution, however, so it stands to reason that each player should attempt to choose his disagreement point in order to maximize his bargaining position. Towards this objective, it is often advantageous to increase one's own disagreement payoff while harming the opponent's disagreement payoff (hence the intrepretation of the disagtreement as a threat). If threats are viewed as actions, then one can construct a separate game wherein each player chooses a threat and receives a payoff according to the outcome of bargaining. It is known as Nash's variable threat game. Alternatively, each player could play a minimaxMinimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
strategy in case of disagreement, choosing to disregard personal reward in order to hurt the opponent as much as possible shoud the opponent leave the bargaining table.
Equilibrium analysis
Strategies are represented in the Nash bargaining game by a pair (x, y). x and y are selected from the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[d, z], where z is the total good. If x + y is equal to or less than z, the first player receives x and the second y. Otherwise both get d. d here represents the disagreement point or the threat of the game; often
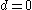.There are many Nash equilibria in the Nash bargaining game. Any x and y such that x + y = z is a Nash equilibrium. If either player increases their demand, both players receive nothing. If either reduces their demand they will receive less than if they had demanded x or y. There is also a Nash equilibrium where both players demand the entire good. Here both players receive nothing, but neither player can increase their return by unilaterally changing their strategy.
Bargaining solutions
Various solutions have been proposed based on slightly different assumptions about what properties are desired for the final agreement point.Nash bargaining solution
John Nash proposed that a solution should satisfy certain axioms:- Invariant to affine transformations or Invariant to equivalent utility representations
- Pareto optimality
- Independence of irrelevant alternativesIndependence of irrelevant alternativesIndependence of irrelevant alternatives is an axiom of decision theory and various social sciences.The word is used in different meanings in different contexts....
- SymmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
Let u and v be the utility functions of Player 1 and Player 2, respectively. In the Nash bargaining solution, the players will seek to maximize
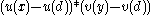, where 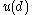and 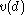, are the status quoStatus quo
Statu quo, a commonly used form of the original Latin "statu quo" – literally "the state in which" – is a Latin term meaning the current or existing state of affairs. To maintain the status quo is to keep the things the way they presently are...
utilities (i.e. the utility obtained if one decides not to bargain with the other player). The product of the two excess utilities is generally referred to as the Nash product.
Kalai-Smorodinsky bargaining solution
Independence of Irrelevant Alternatives can be substituted with a monotonicity condition, as demonstrated by Ehud Kalai and Meir Smorodinsky. It is the point which maintains the ratios of maximal gains. In other words, if player 1 could receive a maximum of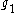 with player 2’s help (and vice-versa for 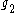), then the Kalai-Smorodinsky bargaining solution would yield the point 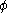on the Pareto frontier such that 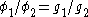.Egalitarian bargaining solution
The egalitarian bargaining solution, introduced by Ehud Kalai, is a third solution which drops the condition of scale invariance while including both the axiom of Independence of irrelevant alternativesIndependence of irrelevant alternatives
Independence of irrelevant alternatives is an axiom of decision theory and various social sciences.The word is used in different meanings in different contexts....
, and the axiom of monotonicity. It is the solution which attempts to grant equal gain to both parties. In other words, it is the point which maximizes the minimum payoff among players.
Applications
Some philosophersPhilosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
and economists
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
have recently used the Nash bargaining game to explain the emergence of human attitudes toward distributive justice
Distributive justice
Distributive justice concerns what some consider to be socially just allocation of goods in a society. A society in which incidental inequalities in outcome do not arise would be considered a society guided by the principles of distributive justice...
(Alexander 2000; Alexander and Skyrms 1999; Binmore 1998, 2005). These authors primarily use evolutionary game theory
Evolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
to explain how individuals come to believe that proposing a 50-50 split is the only just
Justice
Justice is a concept of moral rightness based on ethics, rationality, law, natural law, religion, or equity, along with the punishment of the breach of said ethics; justice is the act of being just and/or fair.-Concept of justice:...
solution to the Nash Bargaining Game.
See also
- BargainingBargainingBargaining or haggling is a type of negotiation in which the buyer and seller of a good or service dispute the price which will be paid and the exact nature of the transaction that will take place, and eventually come to an agreement. Bargaining is an alternative pricing strategy to fixed prices...
- Rubinstein bargaining modelRubinstein bargaining modelA Rubinstein bargaining model refers to a class of bargaining games that feature alternating offers through an infinite time horizon. The original proof is due to Ariel Rubinstein in a 1982 paper...
- Nash equilibriumNash equilibriumIn game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
- Ultimatum gameUltimatum gameThe ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. ...