In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, boxicity is a graph invariant, introduced by Fred S. Roberts

Fred S. Roberts

Fred Stephen Roberts is an American mathematician, a professor of mathematics at Rutgers University and the director of DIMACS.-Biography:...

 in 1969.

The boxicity of a graph is the minimum dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

 in which a given graph can be represented as an intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

 of axis-parallel boxes. That is, there must exist a one-to-one correspondence between the vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 of the graph and a set of boxes, such that two boxes intersect if and only if there is an edge connecting the corresponding vertices.

Examples

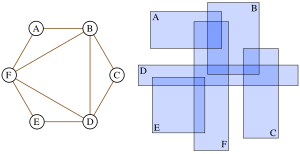
The figure shows a graph with six vertices, and a representation of this graph as an intersection graph of rectangles (two-dimensional boxes). This graph cannot be represented as an intersection graph of boxes in any lower dimension, so its boxicity is two.

showed that the graph with 2n vertices, formed by removing a perfect matching from a complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

 on 2n vertices, has boxicity exactly n: each pair of disconnected vertices must be represented by boxes that are separated in a different dimension than each other pair. A box representation of this graph with dimension exactly n can be found by thickening each of the 2n facets of an n-dimensional hypercube

Hypercube

In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...

 into a box. Because of these results, this graph has been called the Roberts graph, although it is better known as the cocktail party graph and it can also be understood as the Turán graph

Turán graph

The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...

 T(2n,n).

Relation to other graph classes

A graph has boxicity at most one if and only if it is an interval graph

Interval graph

In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...

; the boxicity of an arbitrary graph G is the minimum number of interval graphs on the same set of vertices such that the intersection of the edges sets of the interval graphs is G. Every outerplanar graph

Outerplanar graph

In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...

 has boxicity at most two, and every planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 has boxicity at most three.

If a bipartite graph has boxicity two, it can be represented as an intersection graph of axis-parallel line segments in the plane.

Algorithmic results

Many graph problems can be solved or approximated more efficiently for graphs with bounded boxicity than they can for other graphs; for instance, the maximum clique problem can be solved in polynomial time for graphs with bounded boxicity. For some other graph problems, an efficient solution or approximation can be found if a low-dimensional box representation is known. However, finding such a representation may be difficult:
it is NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

 to test whether the boxicity of a given graph is at most some given value K, even for K = 2.
describe algorithms for finding representations of arbitrary graphs as intersection graphs of boxes, with a dimension that is within a logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

ic factor of the maximum degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

of the graph; this result provides an upper bound on the graph's boxicity.