
Brown's representability theorem
Encyclopedia
In mathematics
, Brown's representability theorem in homotopy theory gives necessary and sufficient conditions on a contravariant functor F on the homotopy category Hot of pointed CW complex
es, to the category of sets
Set, to be a representable functor
. That is, we are given
and certain necessary conditions for F to be of type Hom(—, C) with C a CW-complex can be deduced from category theory
alone. The statement of the substantive part of the theorem is that these necessary conditions are then sufficient. For technical reasons, the theorem is often stated for functors to the category of pointed set
s; in other words the sets are also given a base point.
for any CW complex Z. This isomorphism is natural in Z in that for any morphism from Z to another CW complex Y the induced maps F(Y) → F(Z) and HomHot(Y, C) → HomHot(Z, C) are compatible with these isomorphisms.
According to a combinatorial result in category theory, all small (that is to say, indexed over a set, as opposed to a proper class) colimits are built up from coproduct
s and pushouts
(or just coequalisers). The traditional, equivalent statement of the theorem in algebraic topology
is thus the following: suppose F satisfies the wedge axiom: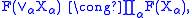
i.e., F converts any wedge sum
(coproduct of pointed space
s) into a product of sets, and the Mayer-Vietoris
axiom, requiring that for any CW complex W covered by two subcomplexes U and V, and any elements u ∈ F(U), v ∈ F(V) such that u and v restrict to the same element of F(U ∩ V), there is an element w ∈ F(W) restricting to u and v, respectively. Under these two conditions, F is representable.
The converse statement also holds: any functor represented by a CW complex satisfies these properties. This direction is an immediate consequence of basic homotopy theory. The deeper and more interesting part of the equivalence is the other implication.
Taking F(X) to be the singular cohomology group Hi(X,A) with coefficients in a given abelian group A, for fixed i > 0; then the representing space for F is the Eilenberg-MacLane space
K(A, i). This gives a means of showing the existence of Eilenberg-MacLane spaces.
instead of CW complexes.
The representing object C above can be shown to depend functorially on F: any natural transformation
from F to another functor satisfying the conditions of the theorem necessarily induces a map of the representing objects. This is a consequence of Yoneda's lemma.
A version of the representability theorem in the case of triangulated categories
is due to Amnon Neeman. Together with the preceding remark, it gives a criterion for a (covariant) functor F: C → D between triangulated categories satisfying certain technical conditions to have a right adjoint functor. Namely, if C and D are triangulated categories with C compactly generated and F a triangulated functor commuting with arbitrary direct sums, then F is a left adjoint. Neeman has applied this to proving the Grothendieck duality theorem in algebraic geometry.
Jacob Lurie
has proved a version of the Brown representability theorem for the homotopy category of a pointed quasicategory with a compact set of generators which are cogroup objects in the homotopy category. For instance, this applies to the homotopy category of (pointed) connected CW complexes, as well as to the unbounded derived category
of a Grothendieck abelian category (in view of Lurie's higher-categorical refinement of the derived category).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Brown's representability theorem in homotopy theory gives necessary and sufficient conditions on a contravariant functor F on the homotopy category Hot of pointed CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
Set, to be a representable functor
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
. That is, we are given
- F: Hotop → Set,
and certain necessary conditions for F to be of type Hom(—, C) with C a CW-complex can be deduced from category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
alone. The statement of the substantive part of the theorem is that these necessary conditions are then sufficient. For technical reasons, the theorem is often stated for functors to the category of pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s; in other words the sets are also given a base point.
Brown representability theorem for CW complexes
The representability theorem for CW complexes, due to E. H. Brown, is the following: suppose the functor F maps any colimit in Hot to a limit in Set. Then F is representable by some CW complex C, that is to say there is an isomorphism- F(Z) ≅ HomHot(Z, C)
for any CW complex Z. This isomorphism is natural in Z in that for any morphism from Z to another CW complex Y the induced maps F(Y) → F(Z) and HomHot(Y, C) → HomHot(Z, C) are compatible with these isomorphisms.
According to a combinatorial result in category theory, all small (that is to say, indexed over a set, as opposed to a proper class) colimits are built up from coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s and pushouts
Pushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
(or just coequalisers). The traditional, equivalent statement of the theorem in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
is thus the following: suppose F satisfies the wedge axiom:
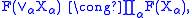
i.e., F converts any wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
(coproduct of pointed space
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s) into a product of sets, and the Mayer-Vietoris
Mayer-Vietoris sequence
In mathematics, particularly algebraic topology and homology theory, the Mayer–Vietoris sequence is an algebraic tool to help compute algebraic invariants of topological spaces, known as their homology and cohomology groups. The result is due to two Austrian mathematicians, Walther Mayer and...
axiom, requiring that for any CW complex W covered by two subcomplexes U and V, and any elements u ∈ F(U), v ∈ F(V) such that u and v restrict to the same element of F(U ∩ V), there is an element w ∈ F(W) restricting to u and v, respectively. Under these two conditions, F is representable.
The converse statement also holds: any functor represented by a CW complex satisfies these properties. This direction is an immediate consequence of basic homotopy theory. The deeper and more interesting part of the equivalence is the other implication.
Taking F(X) to be the singular cohomology group Hi(X,A) with coefficients in a given abelian group A, for fixed i > 0; then the representing space for F is the Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
K(A, i). This gives a means of showing the existence of Eilenberg-MacLane spaces.
Variants
A similar statement holds for spectraSpectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
instead of CW complexes.
The representing object C above can be shown to depend functorially on F: any natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from F to another functor satisfying the conditions of the theorem necessarily induces a map of the representing objects. This is a consequence of Yoneda's lemma.
A version of the representability theorem in the case of triangulated categories
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
is due to Amnon Neeman. Together with the preceding remark, it gives a criterion for a (covariant) functor F: C → D between triangulated categories satisfying certain technical conditions to have a right adjoint functor. Namely, if C and D are triangulated categories with C compactly generated and F a triangulated functor commuting with arbitrary direct sums, then F is a left adjoint. Neeman has applied this to proving the Grothendieck duality theorem in algebraic geometry.
Jacob Lurie
Jacob Lurie
Jacob Alexander Lurie is an American mathematician, who is currently a professor at Harvard University.-Life:While in school, Lurie took part in the International Mathematical Olympiad, where he won a gold medal with a perfect score in 1994...
has proved a version of the Brown representability theorem for the homotopy category of a pointed quasicategory with a compact set of generators which are cogroup objects in the homotopy category. For instance, this applies to the homotopy category of (pointed) connected CW complexes, as well as to the unbounded derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of a Grothendieck abelian category (in view of Lurie's higher-categorical refinement of the derived category).

