Chaitin's constant
Encyclopedia
In the computer science
subfield of algorithmic information theory
, a Chaitin constant or halting probability is a real number
that informally represents the probability
that a randomly constructed program will halt. These numbers are formed from a construction due to Gregory Chaitin
.
Although there are infinitely many halting probabilities, it is common to use the letter Ω to refer to them as if there were only one. Because Ω depends on the program encoding used, it is sometimes called Chaitin's construction instead of Chaitin's constant when not referring to any specific encoding.
Each halting probability is a normal
and transcendental
real number which is not computable
, which means that there is no halting algorithm
that enumerates its digits.
Suppose that F is a partial function that takes one argument, a finite binary string, and possibly returns a single binary string as output. The function F is called computable
if there is a Turing machine
that computes it.
The function F is called universal if the following property holds: for every computable function f of a single variable there is a string w such that for all x, F(w x) = f(x); here w x represents the concatenation
of the two strings w and x. This means that F can be used to simulate any computable function of one variable. Informally, w represents a "script" for the computable function f, and F represents an "interpreter" that parses the script as a prefix of its input and then executes it on the remainder of input.
Note that for any fixed w the function f(x) = F(w x) is computable; thus the universality property states that all computable functions of one variable can be obtained in this fashion.
The domain of F is the set of all inputs p on which it is defined. For F that are universal, such a p can generally be seen both as the concatenation of a program part and a data part, and as a single program for the function F.
The function F is called prefix-free if there are no two elements p, p′ in its domain such that p′ is a proper extension of p. This can be rephrased as: the domain of F is a prefix-free code (instantaneous code) on the set of finite binary strings. A simple way to enforce prefix-free-ness is to use machines whose means of input is a binary stream from which bits can be read one at a time. There is no end-of-stream marker; the end of input is determined by when the universal machine decides to stop reading more bits. Here, the difference between the two notions of program mentioned in the last paragraph becomes clear; the one is easily recognized by some grammar, while the other requires arbitrary computation to recognize.
The domain of any universal computable function is a computably enumerable set but never a computable set. The domain is always Turing equivalent to the halting problem
.
,
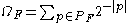where
denotes the length of a string p.
This is an infinite sum
which has one summand for every p in the domain of F. The requirement that the domain be prefix-free, together with Kraft's inequality
, ensures that this sum converges to a real number
between 0 and 1. If F is clear from context then ΩF may be denoted simply Ω, although different prefix-free universal computable functions lead to different values of Ω.
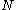bits of 
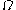, one could calculate the halting problem
for all programs of a size up to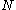
. Let the program 
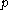for which the halting problem is to be solved be N bits long. In dovetailing
fashion, all programs of all lengths are run, until enough have halted to jointly contribute enough probability to match these first N bits. If the program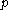
hasn't halted yet, then it never will, since its contribution to the halting probability would affect the first N bits.
Thus, the halting problem would be solved for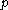
.
Because many outstanding problems in number theory, such as Goldbach's conjecture
are equivalent to solving the halting problem for special programs (which would basically search for counter-examples and halt if one is found), knowing enough bits of Chaitin's constant would also imply knowing the answer to these problems. But as the halting problem is not generally solvable, and therefore calculating any but the first few bits of Chaitin's constant is not possible, this just reduces hard problems to impossible ones, much like trying to build an oracle machine for the halting problem would be.
is the collection of all infinite sequences of 0s and 1s. A halting probability can be interpreted as the measure of a certain subset of Cantor space under the usual probability measure
on Cantor space. It is from this interpretation that halting probabilities take their name.
The probability measure on Cantor space, sometimes called the fair-coin measure, is defined so that for any binary string x the set of sequences that begin with x has measure 2-|x|. This implies that for each natural number n, the set of sequences f in Cantor space such that f(n) = 1 has measure 1/2, and the set of sequences whose nth element is 0 also has measure 1/2.
Let F be a prefix-free universal computable function. The domain P of F consists of an infinite set of binary strings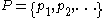
.
Each of these strings pi determines a subset Si of Cantor space; the set Si contains all sequences in cantor space that begin with pi. These sets are disjoint because P is a prefix-free set. The sum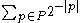
represents the measure of the set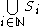
.
In this way, ΩF represents the probability that a randomly selected infinite sequence of 0s and 1s begins with a bit string (of some finite length) that is in the domain of F. It is for this reason that ΩF is called a halting probability.
Not every set that is Turing equivalent to the halting problem is a halting probability. A finer equivalence relation, Solovay equivalence, can be used to characterize the halting probabilities among the left-c.e. reals.
No halting probability is computable. The proof of this fact relies on an algorithm which, given the first n digits of Ω, solves Turing's halting problem
for programs of length up to n. Since the halting problem is undecidable
, Ω can not be computed.
The algorithm proceeds as follows. Given the first n digits of Ω and a k≤n, the algorithm enumerates the domain of F until enough elements of the domain have been found so that the probability they represent is within 2-(k+1) of Ω. After this point, no additional program of length k can be in the domain, because each of these would add 2-k to the measure, which is impossible. Thus the set of strings of length k in the domain is exactly the set of such strings already enumerated.
for the natural numbers, such as Peano arithmetic
, there exists a constant N such that no bit of Ω after the Nth can be proven to be one or zero within that system. The constant N depends on how the formal system
is effectively represented, and thus does not directly reflect the complexity of the axiomatic system. This incompleteness result is similar to Gödel's incompleteness theorem in that it shows that no consistent formal theory for arithmetic can be complete.
's constant Omega are random or incompressible in the sense that we cannot compute them by a halting algorithm with fewer than n-O(1) bits. However, consider the short but never halting algorithm which systematically lists and runs all possible programs; whenever one of them halts its probability gets added to the output (initialized by zero). After finite time the first n bits of the output will never change any more (it does not matter that this time itself is not computable by a halting program). So there is a short non-halting algorithm whose output converges (after finite time) onto the first n bits of Omega. In other words, the enumerable first n bits of Omega are highly compressible in the sense that they are limit-computable by a very short algorithm; they are not random with respect to the set of enumerating algorithms. Jürgen Schmidhuber
(2000) constructed a limit-computable "Super Omega" which in a sense is much more random than the original limit-computable Omega, as one cannot significantly compress the Super Omega by any enumerating non-halting algorithm.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
subfield of algorithmic information theory
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
, a Chaitin constant or halting probability is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
that informally represents the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that a randomly constructed program will halt. These numbers are formed from a construction due to Gregory Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
.
Although there are infinitely many halting probabilities, it is common to use the letter Ω to refer to them as if there were only one. Because Ω depends on the program encoding used, it is sometimes called Chaitin's construction instead of Chaitin's constant when not referring to any specific encoding.
Each halting probability is a normal
Normal number
In mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
and transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
real number which is not computable
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
, which means that there is no halting algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that enumerates its digits.
Background
The definition of a halting probability relies on the existence of prefix-free universal computable functions. Such a function, intuitively, represents a programming language with the property that no valid program can be obtained as a proper extension of another valid program.Suppose that F is a partial function that takes one argument, a finite binary string, and possibly returns a single binary string as output. The function F is called computable
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
if there is a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
that computes it.
The function F is called universal if the following property holds: for every computable function f of a single variable there is a string w such that for all x, F(w x) = f(x); here w x represents the concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
of the two strings w and x. This means that F can be used to simulate any computable function of one variable. Informally, w represents a "script" for the computable function f, and F represents an "interpreter" that parses the script as a prefix of its input and then executes it on the remainder of input.
Note that for any fixed w the function f(x) = F(w x) is computable; thus the universality property states that all computable functions of one variable can be obtained in this fashion.
The domain of F is the set of all inputs p on which it is defined. For F that are universal, such a p can generally be seen both as the concatenation of a program part and a data part, and as a single program for the function F.
The function F is called prefix-free if there are no two elements p, p′ in its domain such that p′ is a proper extension of p. This can be rephrased as: the domain of F is a prefix-free code (instantaneous code) on the set of finite binary strings. A simple way to enforce prefix-free-ness is to use machines whose means of input is a binary stream from which bits can be read one at a time. There is no end-of-stream marker; the end of input is determined by when the universal machine decides to stop reading more bits. Here, the difference between the two notions of program mentioned in the last paragraph becomes clear; the one is easily recognized by some grammar, while the other requires arbitrary computation to recognize.
The domain of any universal computable function is a computably enumerable set but never a computable set. The domain is always Turing equivalent to the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
.
Definition
Let PF be the domain of a prefix-free universal computable function F. The constant ΩF is then defined as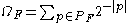,where
denotes the length of a string p.This is an infinite sum
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
which has one summand for every p in the domain of F. The requirement that the domain be prefix-free, together with Kraft's inequality
Kraft's inequality
In coding theory, Kraft's inequality, named after Leon Kraft, gives a necessary and sufficient condition for the existence of a uniquely decodable code for a given set of codeword lengths...
, ensures that this sum converges to a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
between 0 and 1. If F is clear from context then ΩF may be denoted simply Ω, although different prefix-free universal computable functions lead to different values of Ω.
Relationship to the halting problem
Knowing the first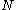 bits of 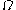, one could calculate the halting problemHalting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
for all programs of a size up to
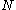. Let the program 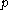for which the halting problem is to be solved be N bits long. In dovetailingDovetailing (computer science)
Dovetailing in algorithm design, is a technique that interleaves different computations, performing them essentially simultaneously. Algorithms that use dovetailing are sometimes referred to as dovetailers....
fashion, all programs of all lengths are run, until enough have halted to jointly contribute enough probability to match these first N bits. If the program
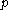hasn't halted yet, then it never will, since its contribution to the halting probability would affect the first N bits.Thus, the halting problem would be solved for
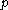.Because many outstanding problems in number theory, such as Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
are equivalent to solving the halting problem for special programs (which would basically search for counter-examples and halt if one is found), knowing enough bits of Chaitin's constant would also imply knowing the answer to these problems. But as the halting problem is not generally solvable, and therefore calculating any but the first few bits of Chaitin's constant is not possible, this just reduces hard problems to impossible ones, much like trying to build an oracle machine for the halting problem would be.
Interpretation as a probability
The Cantor spaceCantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
is the collection of all infinite sequences of 0s and 1s. A halting probability can be interpreted as the measure of a certain subset of Cantor space under the usual probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on Cantor space. It is from this interpretation that halting probabilities take their name.
The probability measure on Cantor space, sometimes called the fair-coin measure, is defined so that for any binary string x the set of sequences that begin with x has measure 2-|x|. This implies that for each natural number n, the set of sequences f in Cantor space such that f(n) = 1 has measure 1/2, and the set of sequences whose nth element is 0 also has measure 1/2.
Let F be a prefix-free universal computable function. The domain P of F consists of an infinite set of binary strings
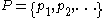.Each of these strings pi determines a subset Si of Cantor space; the set Si contains all sequences in cantor space that begin with pi. These sets are disjoint because P is a prefix-free set. The sum
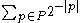
represents the measure of the set
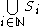.In this way, ΩF represents the probability that a randomly selected infinite sequence of 0s and 1s begins with a bit string (of some finite length) that is in the domain of F. It is for this reason that ΩF is called a halting probability.
Properties
Each Chaitin constant Ω has the following properties:- It is algorithmically random. This means that the shortest program to output the first n bits of Ω must be of size at least n-O(1). This is because, as in the Goldbach example, those n bits enable us to find out exactly which programs halt among all those of length at most n.
- It is a normal numberNormal numberIn mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
, which means that its digits are equidistributed as if they were generated by tossing a fair coin. - It is not a computable numberComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
; there is no computable function that enumerates its binary expansion, as discussed below. - The set of rational numbers q such that q ≤ Ω is computably enumerable; a real number with such a property is called a left-c.e. real number in recursion theoryRecursion theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
. - It is Turing equivalent to the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
and thus at level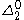
of the arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
.
Not every set that is Turing equivalent to the halting problem is a halting probability. A finer equivalence relation, Solovay equivalence, can be used to characterize the halting probabilities among the left-c.e. reals.
Uncomputability
A real number is called computable if there is an algorithm which, given n, returns the first n digits of the number. This is equivalent to the existence of a program that enumerates the digits of the real number.No halting probability is computable. The proof of this fact relies on an algorithm which, given the first n digits of Ω, solves Turing's halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
for programs of length up to n. Since the halting problem is undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
, Ω can not be computed.
The algorithm proceeds as follows. Given the first n digits of Ω and a k≤n, the algorithm enumerates the domain of F until enough elements of the domain have been found so that the probability they represent is within 2-(k+1) of Ω. After this point, no additional program of length k can be in the domain, because each of these would add 2-k to the measure, which is impossible. Thus the set of strings of length k in the domain is exactly the set of such strings already enumerated.
Incompleteness theorem for halting probabilities
For each specific consistent effectively represented axiomatic systemAxiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
for the natural numbers, such as Peano arithmetic
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
, there exists a constant N such that no bit of Ω after the Nth can be proven to be one or zero within that system. The constant N depends on how the formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
is effectively represented, and thus does not directly reflect the complexity of the axiomatic system. This incompleteness result is similar to Gödel's incompleteness theorem in that it shows that no consistent formal theory for arithmetic can be complete.
Super Omega
As mentioned above, the first n bits of Gregory ChaitinGregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
's constant Omega are random or incompressible in the sense that we cannot compute them by a halting algorithm with fewer than n-O(1) bits. However, consider the short but never halting algorithm which systematically lists and runs all possible programs; whenever one of them halts its probability gets added to the output (initialized by zero). After finite time the first n bits of the output will never change any more (it does not matter that this time itself is not computable by a halting program). So there is a short non-halting algorithm whose output converges (after finite time) onto the first n bits of Omega. In other words, the enumerable first n bits of Omega are highly compressible in the sense that they are limit-computable by a very short algorithm; they are not random with respect to the set of enumerating algorithms. Jürgen Schmidhuber
Jürgen Schmidhuber
Jürgen Schmidhuber is a computer scientist and artist known for his work on machine learning, universal Artificial Intelligence , artificial neural networks, digital physics, and low-complexity art. His contributions also include generalizations of Kolmogorov complexity and the Speed Prior...
(2000) constructed a limit-computable "Super Omega" which in a sense is much more random than the original limit-computable Omega, as one cannot significantly compress the Super Omega by any enumerating non-halting algorithm.
External links
- Omega and why maths has no TOEs article based on one written by Gregory ChaitinGregory ChaitinGregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
which appeared in the August 2004 edition of Mathematics Today, on the occasion of the 50th anniversary of Alan Turing's death. - The Limits of Reason, Gregory Chaitin, originally appeared in Scientific American, March 2006.
- Limit-computable Super Omega more random than Omega and generalizations of algorithmic information, by Jürgen SchmidhuberJürgen SchmidhuberJürgen Schmidhuber is a computer scientist and artist known for his work on machine learning, universal Artificial Intelligence , artificial neural networks, digital physics, and low-complexity art. His contributions also include generalizations of Kolmogorov complexity and the Speed Prior...