Checking if a coin is fair
Encyclopedia
In statistics
, the question of checking whether a coin is fair is one whose importance lies, firstly, in providing a simple problem on which to illustrate basic ideas of statistical inference
and, secondly, in providing a simple problem that can be used to compare various competing methods of statistical inference, including decision theory
. The practical problem of checking whether a coin is fair might be considered as easily solved by performing a sufficiently large number of trials, but statistics and probability theory
can provide guidance on two types of question; specifically those of how many trials to undertake and of the accuracy an estimate of the probability of turning up heads, derived from a given sample of trials.
A fair coin
is an idealized randomizing device
with two states (usually named "heads" and "tails") which are equally likely to occur. It is based on the coin flip used widely in sports and other situations where it is required to give two parties the same chance of winning. Either a specially designed chip
or more usually a simple currency coin
is used, although the latter might be slightly "unfair" due to an asymmetrical weight distribution, which might cause one state to occur more frequently than the other, giving one party an unfair advantage. So it might be necessary to test experimentally whether the coin is in fact "fair" – that is, whether the probability of the coin falling on either side when it is tossed is approximately 50%. It is of course impossible to rule out arbitrarily small deviations from fairness such as might be expected to affect only one flip in a lifetime of flipping; also it is always possible for an unfair (or "biased") coin to happen to turn up exactly 10 heads in 20 flips. As such, any fairness test must only establish a certain degree of confidence in a certain degree of fairness (a certain maximum bias). In more rigorous terminology, the problem is of determining the parameters of a Bernoulli process
, given only a limited sample of Bernoulli trial
s.
Both methods prescribe an experiment (or trial) in which the coin is tossed many times and the result of each toss is recorded. The results can then be analysed statistically to decide whether the coin is "fair" or "probably not fair". It is assumed that the number of tosses is fixed and cannot be decided by the experimenter.
An important difference between these two approaches is that the first approach gives some weight to one's prior experience of tossing coins, while the second does not. The question of how much weight to give to prior experience, depending on the quality (credibility) of that experience, is discussed under credibility theory
.
of Bayesian probability theory.
A test is performed by tossing the coin N times and noting the observed numbers of heads, h, and tails, t. The symbols H and T represent more generalised variables expressing the numbers of heads and tails respectively that might have been observed in the experiment. Thus N = H+T = h+t.
Next, let r be the actual probability of obtaining heads in a single toss of the coin. This is the property of the coin which is being investigated. Using Bayes' theorem
, the posterior probability density of r conditional on h and t is expressed as follows:
where g(r) represents the prior probability density distribution of r, which lies in the range 0 to 1.
The prior probability density distribution summarizes what is known about the distribution of r in the absence of any observation. We will assume that the prior distribution of r is uniform
over the interval [0, 1]. That is, g(r) = 1. (In practice, it would be more appropriate to assume a prior distribution which is much more heavily weighted in the region around 0.5, to reflect our experience with real coins.)
The probability of obtaining h heads in N tosses of a coin with a probability of heads equal to r is given by the binomial distribution:
Substituting this into the previous formula:
This is in fact a beta distribution (the conjugate prior
for the binomial distribution), whose denominator can be expressed in terms of the beta function:
As a uniform prior distribution has been assumed, and because h and t are integers, this can also be written in terms of factorial
s:
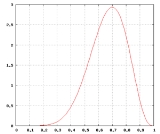
The graph on the right shows the probability density function
of r given that 7 heads were obtained in 10 tosses. (Note: r is the probability of obtaining heads when tossing the same coin once.)
The probability for an unbiased coin (defined for this purpose as one whose probability of coming down heads is somewhere between 45% and 55%)
is small when compared with the alternative hypothesis (a biased coin). However, it is not small enough to cause us to believe that the coin has a significant bias. Notice that this probability is slightly higher than our presupposition of the probability that the coin was fair corresponding to the uniform prior distribution, which was 10%.
Using a prior distribution that reflects our prior knowledge of what a coin is and how it acts, the posterior distribution would not favor the hypothesis of bias. However the number of trials in this example (10 tosses) is very small, and with more trials the choice of prior distribution would be somewhat less relevant.)
Note that, with the uniform prior, the posterior probability distribution f(r | H = 7,T = 3) achieves its peak at r = h / (h + t) = 0.7; this value is called the maximum a posteriori (MAP) estimate of r. Also with the uniform prior, the expected value
of r under the posterior distribution is
Using this approach, to decide the number of times the coin should be tossed, two parameters are required:
where n is the number of trials (which was denoted by N in the previous paragraph).
This standard error
function of p has a maximum at 
. Further, in the case of a coin being tossed, it is likely that p will be not far from 0.5, so it is reasonable to take p=0.5 in the following:
And hence the value of maximum error (E) is given by
Solving for the required number of coin tosses, n,
at 68.27% level of confidence (Z=1)
at 95.45% level of confidence (Z=2)
at 99.90% level of confidence (Z=3.3)
2. If the coin is tossed 10000 times, what is the maximum error of the estimator
on the value of 
(the actual probability of obtaining heads in a coin toss)?
at 68.27% level of confidence (Z=1)
at 95.45% level of confidence (Z=2)
at 99.90% level of confidence (Z=3.3)
3. The coin is tossed 12000 times with a result of 5961 heads (and 6039 tails). What interval does the value of
(the true probability of obtaining heads) lie within if a confidence level of 99.999% is desired?
Now find the value of Z corresponding to 99.999% level of confidence.
Now calculate E
The interval which contains r is thus:
Hence, 99.999% of the time, the interval above would contain
which is the true value of obtaining heads in a single toss.
, whose application would require the formulation of a loss function
or utility function which describes the consequences of making a given decision. An approach that avoids requiring either a loss function or a prior probability (as in the Bayesian approach) is that of "acceptance sampling".
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the question of checking whether a coin is fair is one whose importance lies, firstly, in providing a simple problem on which to illustrate basic ideas of statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
and, secondly, in providing a simple problem that can be used to compare various competing methods of statistical inference, including decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
. The practical problem of checking whether a coin is fair might be considered as easily solved by performing a sufficiently large number of trials, but statistics and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
can provide guidance on two types of question; specifically those of how many trials to undertake and of the accuracy an estimate of the probability of turning up heads, derived from a given sample of trials.
A fair coin
Fair coin
In probability theory and statistics, a sequence of independent Bernoulli trials with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin...
is an idealized randomizing device
Statistical randomness
A numeric sequence is said to be statistically random when it contains no recognizable patterns or regularities; sequences such as the results of an ideal dice roll, or the digits of π exhibit statistical randomness....
with two states (usually named "heads" and "tails") which are equally likely to occur. It is based on the coin flip used widely in sports and other situations where it is required to give two parties the same chance of winning. Either a specially designed chip
Casino token
Casino tokens are small discs used in lieu of currency in casinos. Colored metal, injection molded plastic or compression molded clay tokens of various denominations are used primarily in table games, as opposed to metal token coins, used primarily in slot machines...
or more usually a simple currency coin
Coin
A coin is a piece of hard material that is standardized in weight, is produced in large quantities in order to facilitate trade, and primarily can be used as a legal tender token for commerce in the designated country, region, or territory....
is used, although the latter might be slightly "unfair" due to an asymmetrical weight distribution, which might cause one state to occur more frequently than the other, giving one party an unfair advantage. So it might be necessary to test experimentally whether the coin is in fact "fair" – that is, whether the probability of the coin falling on either side when it is tossed is approximately 50%. It is of course impossible to rule out arbitrarily small deviations from fairness such as might be expected to affect only one flip in a lifetime of flipping; also it is always possible for an unfair (or "biased") coin to happen to turn up exactly 10 heads in 20 flips. As such, any fairness test must only establish a certain degree of confidence in a certain degree of fairness (a certain maximum bias). In more rigorous terminology, the problem is of determining the parameters of a Bernoulli process
Bernoulli process
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
, given only a limited sample of Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s.
Preamble
This article describes experimental procedures for determining whether a coin is fair or not fair. There are many statistical methods for analyzing such an experimental procedure. This article illustrates two of them.Both methods prescribe an experiment (or trial) in which the coin is tossed many times and the result of each toss is recorded. The results can then be analysed statistically to decide whether the coin is "fair" or "probably not fair". It is assumed that the number of tosses is fixed and cannot be decided by the experimenter.
- Posterior probability density function, or PDF (Bayesian approachBayesian probabilityBayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
). The true probability of obtaining a particular side when a fair coin is tossed is unknown, but the uncertainty is initially represented by the "prior distribution". The theory of Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
is used to derive the posterior distribution by combining the prior distribution and the likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
which represents the information obtained from the experiment. The probability that this particular coin is a "fair coin" can then be obtained by integrating the PDF of the posterior distribution over the relevant interval that represents all the probabilities that can be counted as "fair" in a practical sense.
- Estimator of true probability (Frequentist approachFrequency probabilityFrequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
). This method assumes that the experimenter can decide to toss the coin any number of times. He first decides on the level of confidence required and the tolerable margin of error. These parameters determine the minimum number of tosses that must be performed to complete the experiment.
An important difference between these two approaches is that the first approach gives some weight to one's prior experience of tossing coins, while the second does not. The question of how much weight to give to prior experience, depending on the quality (credibility) of that experience, is discussed under credibility theory
Credibility Theory
Credibility theory is a branch of actuarial science. It was developed originally as a method to calculate the risk premium by combining the individual risk experience with the class risk experience....
.
Posterior probability density function
One method is to calculate the posterior probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of Bayesian probability theory.
A test is performed by tossing the coin N times and noting the observed numbers of heads, h, and tails, t. The symbols H and T represent more generalised variables expressing the numbers of heads and tails respectively that might have been observed in the experiment. Thus N = H+T = h+t.
Next, let r be the actual probability of obtaining heads in a single toss of the coin. This is the property of the coin which is being investigated. Using Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, the posterior probability density of r conditional on h and t is expressed as follows:
where g(r) represents the prior probability density distribution of r, which lies in the range 0 to 1.
The prior probability density distribution summarizes what is known about the distribution of r in the absence of any observation. We will assume that the prior distribution of r is uniform
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
over the interval [0, 1]. That is, g(r) = 1. (In practice, it would be more appropriate to assume a prior distribution which is much more heavily weighted in the region around 0.5, to reflect our experience with real coins.)
The probability of obtaining h heads in N tosses of a coin with a probability of heads equal to r is given by the binomial distribution:
Substituting this into the previous formula:
This is in fact a beta distribution (the conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for the binomial distribution), whose denominator can be expressed in terms of the beta function:
As a uniform prior distribution has been assumed, and because h and t are integers, this can also be written in terms of factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s:
Example
For example, let N = 10, h = 7, i.e. the coin is tossed 10 times and 7 heads are obtained:The graph on the right shows the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of r given that 7 heads were obtained in 10 tosses. (Note: r is the probability of obtaining heads when tossing the same coin once.)
is small when compared with the alternative hypothesis (a biased coin). However, it is not small enough to cause us to believe that the coin has a significant bias. Notice that this probability is slightly higher than our presupposition of the probability that the coin was fair corresponding to the uniform prior distribution, which was 10%.
Using a prior distribution that reflects our prior knowledge of what a coin is and how it acts, the posterior distribution would not favor the hypothesis of bias. However the number of trials in this example (10 tosses) is very small, and with more trials the choice of prior distribution would be somewhat less relevant.)
Note that, with the uniform prior, the posterior probability distribution f(r | H = 7,T = 3) achieves its peak at r = h / (h + t) = 0.7; this value is called the maximum a posteriori (MAP) estimate of r. Also with the uniform prior, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of r under the posterior distribution is
Estimator of true probability
is the estimator  .This estimator has a margin of error (E) where  at a particular confidence level. |
Using this approach, to decide the number of times the coin should be tossed, two parameters are required:
- The confidence level which is denoted by confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
(Z) - The maximum (acceptable) error (E)
- The confidence level is denoted by Z and is given by the Z-value of a standard normal distribution. This value can be read off a standard scoreStandard scoreIn statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
statistics table for the normal distribution. Some examples are:
| Z value | Confidence Level | Comment |
|---|---|---|
| 0.6745 | gives 50.000% level of confidence | Half |
| 1.0000 | gives 68.269% level of confidence | One std dev |
| 1.6449 | gives 90.000% level of confidence | "One Nine" |
| 1.9599 | gives 95.000% level of confidence | 95 percent |
| 2.0000 | gives 95.450% level of confidence | Two std dev |
| 2.5759 | gives 99.000% level of confidence | "Two Nines" |
| 3.0000 | gives 99.730% level of confidence | Three std dev |
| 3.2905 | gives 99.900% level of confidence | "Three Nines" |
| 3.8906 | gives 99.990% level of confidence | "Four Nines" |
| 4.0000 | gives 99.993% level of confidence | Four std dev |
| 4.4172 | gives 99.999% level of confidence | "Five Nines" |
- The maximum error (E) is defined by
where 
is the estimated probability of obtaining heads. Note: 
is the same actual probability (of obtaining heads) as 
of the previous section in this article.
- In statistics, the estimate of a proportion of a sample (denoted by p) has a standard error (standard deviation of error) given by:
where n is the number of trials (which was denoted by N in the previous paragraph).
This standard error
function of p has a maximum at . Further, in the case of a coin being tossed, it is likely that p will be not far from 0.5, so it is reasonable to take p=0.5 in the following: |
 |
And hence the value of maximum error (E) is given by
 |
 |
Solving for the required number of coin tosses, n,
Examples
1. If a maximum error of 0.01 is desired, how many times should the coin be tossed? at 68.27% level of confidence (Z=1) at 95.45% level of confidence (Z=2) at 99.90% level of confidence (Z=3.3)2. If the coin is tossed 10000 times, what is the maximum error of the estimator
on the value of (the actual probability of obtaining heads in a coin toss)? at 68.27% level of confidence (Z=1) at 95.45% level of confidence (Z=2) at 99.90% level of confidence (Z=3.3)3. The coin is tossed 12000 times with a result of 5961 heads (and 6039 tails). What interval does the value of
(the true probability of obtaining heads) lie within if a confidence level of 99.999% is desired?Now find the value of Z corresponding to 99.999% level of confidence.
Now calculate E
The interval which contains r is thus:
Hence, 99.999% of the time, the interval above would contain
which is the true value of obtaining heads in a single toss.Other approaches
Other approaches to the question of checking whether a coin is fair are available using decision theoryDecision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, whose application would require the formulation of a loss function
Loss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
or utility function which describes the consequences of making a given decision. An approach that avoids requiring either a loss function or a prior probability (as in the Bayesian approach) is that of "acceptance sampling".
Other applications
The above mathematical analysis for determining if a coin is fair can also be applied to other uses. For example:- Determining the proportion of defective items for a product subjected to a particular (but well defined) condition. Sometimes a product can be very difficult or expensive to produce. Furthermore, if testing such products will result in their destruction, a minimum number of items should be tested. Using a similar analysis, the probability density function of the product defect rate can be found.
- Two party polling. If a small random sample poll is taken where there are only two mutually exclusive choices, then this is similar to tossing a single coin multiple times using a possibly biased coin. A similar analysis can therefore be applied to determine the confidence to be ascribed to the actual ratio of votes cast. (Note that if people are allowed to abstain then the analysis must take account of that, and the coin-flip analogy doesn't quite hold.)
- Finding the proportion of females in an animal group. Determining the gender ratio in a large group of an animal species. Provided that a small random sample (i.e. small in comparison with the total population) is taken when performing the random sampling of the population, the analysis is similar to determining the probability of obtaining heads in a coin toss.
See also
- Binomial testBinomial testIn statistics, the binomial test is an exact test of the statistical significance of deviations from a theoretically expected distribution of observations into two categories.-Common use:...
- Coin flippingCoin flippingCoin flipping or coin tossing or heads or tails is the practice of throwing a coin in the air to choose between two alternatives, sometimes to resolve a dispute between two parties...
- Confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
- Estimation theoryEstimation theoryEstimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
- Inferential statistics
- Dice#Loaded dice
- Margin of errorMargin of errorThe margin of error is a statistic expressing the amount of random sampling error in a survey's results. The larger the margin of error, the less faith one should have that the poll's reported results are close to the "true" figures; that is, the figures for the whole population...
- Point estimationPoint estimationIn statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter....
- Statistical randomnessStatistical randomnessA numeric sequence is said to be statistically random when it contains no recognizable patterns or regularities; sequences such as the results of an ideal dice roll, or the digits of π exhibit statistical randomness....