Cone (formal languages)
Encyclopedia
In formal language theory, a cone is a set of formal languages
that has some desirable closure
properties enjoyed by some well-known sets of languages, in particular by the families of regular languages
, context-free languages
and the recursive languages
. The concept of a cone is a more abstract notion that subsumes all of these families.
More precisely, a cone is a non-empty family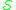
of languages such that, for any 
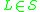over some alphabet 
,
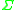The family of all regular languages is contained in any cone.
If one restricts the definition to homomorphisms that do not introduce the empty word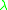
then one speaks of a faithful cone; the inverse homomorphisms are not restricted. Within the Chomsky hierarchy
, the regular languages, the context-free languages, and the recursively enumerable language
s are all cones, whereas the context sensitive languages and the recursive languages are only faithful cones.
The terminology cone has a French origin. In the American oriented literature one usually speaks of a full trio. The trio corresponds to the faithful cone.
is a finite state automaton that has both input and output. It defines a transduction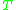
, mapping a language 
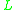over the input alphabet into another language 
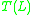over the output alphabet. Each of the cone operations (homomorphism, inverse homomorphism, intersection with a regular language) can be implemented using a finite state transducer. And, since finite state transducers are closed under composition, every sequence of cone operations can be performed by a finite state transducer.
Conversely, every finite state transduction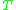
can be decomposed into cone operations. In fact, there exists a normal form for this decomposition, which is commonly known as Nivat's Theorem:
Namely, each such T can be effectively decomposed as
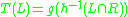, where 
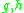are homomorphisms, and 
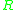is a regular language depending only on 
.
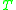Altogether, this means that a family of languages is a cone if it is closed under finite state transductions. This is a very powerful set of operations. For instance one easily writes a (nondeterministic) finite state transducer with alphabet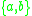
that removes every second 
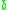in words of even length (and does not change words otherwise). Since the context-free languages form a cone, they are closed under this exotic operation.
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
that has some desirable closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
properties enjoyed by some well-known sets of languages, in particular by the families of regular languages
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
, context-free languages
Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
and the recursive languages
Recursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
. The concept of a cone is a more abstract notion that subsumes all of these families.
More precisely, a cone is a non-empty family
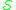of languages such that, for any 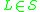over some alphabet ,
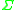- if
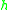is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from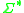
to some 
, the language 
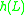is in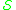 
; - if
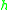is a homomorphism from some 
to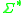 
, the language 
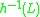is in 
; - if
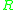is any regular language over 
, then 
is in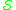 
.
The family of all regular languages is contained in any cone.
If one restricts the definition to homomorphisms that do not introduce the empty word
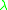then one speaks of a faithful cone; the inverse homomorphisms are not restricted. Within the Chomsky hierarchyChomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
, the regular languages, the context-free languages, and the recursively enumerable language
Recursively enumerable language
In mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy of formal languages...
s are all cones, whereas the context sensitive languages and the recursive languages are only faithful cones.
The terminology cone has a French origin. In the American oriented literature one usually speaks of a full trio. The trio corresponds to the faithful cone.
Relation to Transducers
A finite state transducerFinite state transducer
A finite state transducer is a finite state machine with two tapes: an input tape and an output tape. This contrasts with an ordinary finite state automaton , which has a single tape.-Overview:...
is a finite state automaton that has both input and output. It defines a transduction
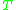, mapping a language 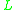over the input alphabet into another language 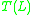over the output alphabet. Each of the cone operations (homomorphism, inverse homomorphism, intersection with a regular language) can be implemented using a finite state transducer. And, since finite state transducers are closed under composition, every sequence of cone operations can be performed by a finite state transducer.Conversely, every finite state transduction
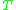can be decomposed into cone operations. In fact, there exists a normal form for this decomposition, which is commonly known as Nivat's Theorem:Namely, each such T can be effectively decomposed as
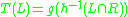, where 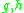are homomorphisms, and 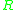is a regular language depending only on 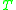.Altogether, this means that a family of languages is a cone if it is closed under finite state transductions. This is a very powerful set of operations. For instance one easily writes a (nondeterministic) finite state transducer with alphabet
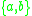that removes every second 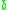in words of even length (and does not change words otherwise). Since the context-free languages form a cone, they are closed under this exotic operation.External links
- Encyclopedia of mathematics: Trio, Springer.