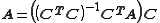
Determination of equilibrium constants
Encyclopedia
Equilibrium constants are determined in order to quantify chemical equilibria. When an equilibrium constant is expressed as a concentration quotient,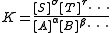
it is implied that the activity
quotient is constant. In order for this assumption to be valid equilibrium constants should be determined in a medium of relatively high ionic strength
. Where this is not possible, consideration should be given to possible activity variation.
The equilibrium expression above is a function of the concentration
s [A], [B] etc. of the chemical species in equilibrium. The equilibrium constant value can be determined if any one of these concentrations can be measured. The general procedure is that the concentration in question is measured for a series of solutions with known analytical concentrations of the reactants. Typically, a titration
is performed with one or more reactants in the titration vessel and one or more reactants in the burette. Knowing the analytical concentrations of reactants initially in the reaction vessel and in the burette, all analytical concentrations can be derived as a function of the volume (or mass) of titrant added.
The equilibrium constants may be derived by best-fitting of the experimental data with a chemical model of the equilibrium system.
such as the glass electrode
. If the electrode is calibrated using activity standards it is assumed that the Nernst equation
applies in the form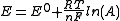
where E0 is the standard electrode potential
. When buffer
solutions of known pH are used for calibration the meter
reading will be pH.
At 298K, 1 pH unit is approximately equal to 59 mV.
When the electrode is calibrated with solutions of known concentration, by means of a strong acid/strong base titration, for example, a modified Nernst equation is assumed.
s an empirical slope factor. A solution of known hydrogen ion concentration may be prepared by standardization of a strong acid
against borax
. Constant-boiling
hydrochloric acid
may also be used as a primary standard for hydrogen ion concentration.
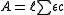
where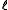
is the optical path length, 
is a molar absorbance at unit path length and c is a concentration. More than one of the species may contribute to the absorbance. In principle absorbance may be measured at one wavelength only, but in present-day practice it is common to record complete spectra.
where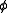
is a proportionality constant.
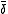is the mole-fraction-weighted average of the shifts 
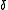of nuclei in contributing species.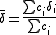
H for 1:1 adducts is routinely carried out using Isothermal Titration Calorimetry
. Extension to more complex systems is limited by the availability of suitable software.
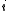-th data point, the analytical concentrations of the reactants, 
, 
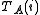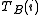etc. are known along with a measured quantity, 
, that depends on one or more of these analytical concentrations. A general computational procedure has three main components.
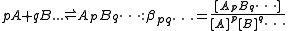
When using general-purpose computer programs, it is usual to use cumulative, association constants, as shown above. Electrical charges are not shown in general expressions such as this and are often omitted from specific expressions, for simplicity of notation. In fact, electrical charges have no bearing on the equilibrium processes other that there being a requirement for overall electrical neutrality in all systems.
With aqueous solutions the concentrations of proton (hydronium ion) and hydroxide ion are constrained by the self-dissociation of water.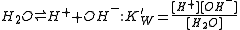
With dilute solutions the concentration of water can be assumed to be constant so the equilibrium expression is written in the familiar form of the ionic product
of water.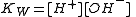
When both H+ and OH− must be considered as reactants, one of them is eliminated from the model by specifying that its concentration is to be derived from the concentration of the other. Usually the concentration of the hydroxide ion is given by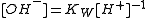
In this case the equilibrium constant for the formation of hydroxide has the stoichiometric coefficients −1 in regard to the proton and zero for the other reactants. This has important implications for all protonation equilibria in aqueous solution and for hydrolysis constants in particular.
It is quite usual to omit from the model those species whose concentrations are considered to be negligible. For example it is usually assumed then there is no interaction between the reactants and/or complexes and the electrolyte used to maintain constant ionic strength or the buffer used to maintain constant pH. These assumptions may or may not be justified. Also, it is implicitly assumed that there are no other complex species present. When complexes are wrongly ignored a systematic error
is introduced into the calculations.
Equilibrium constant values are usually estimated initially by reference to data sources.
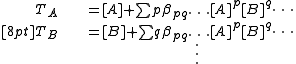
for the free concentrations [A], [B] etc. The concentrations of the complexes are derived from the free concentrations via the chemical model. Some authors include the free reactant terms in the sums by declaring identity (unit)
constants for which the stoichiometric coefficients are 1 for the reactant concerned and zero for all other reactants:
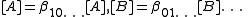
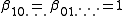
In this manner, all chemical species, including the free reactants, are treated in the same way, having been formed from the combination of reactants that is specified by the stoichiometric coefficients. The mass-balance equations assume the simpler form.
In a titration system the analytical concentrations of the reactants at each titration point are obtained from the initial conditions, the burette concentrations and volumes. The analytical (total) concentration of a reactant R at the ith titration point is given by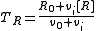
where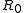
is the initial amount of R in the titration vessel, 
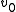is the initial volume, 
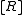is the concentration of R in the burette and 
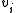is the volume added. The burette concentration of a reactant not present in the burette is taken to be zero.
In general, solving these non-linear equations presents a formidable challenge because of the huge range over which the free concentrations may vary. At the beginning, values for the free concentrations must be estimated. Then, these values are refined, usually by means of Newton–Raphson
iterations. The logarithms of the free concentrations may be refined rather than the free concentrations themselves. Refinement of the logarithms of the free concentrations has the added advantage of automatically imposing a non-negativity constraint on the free concentrations. Once the free reactant concentrations have been calculated, the concentrations of the complexes are derived from them and the equilibrium constants.
Note that the free reactant concentrations can be regarded as implicit parameters in the equilibrium constant refinement process. In that context the values of the free concentrations are constrained by forcing the conditions of mass-balance to apply at all stages of the process.
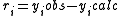
Then the most general objective function is given by
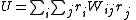
The matrix of weights, W, should be, ideally, the inverse of the variance-covariance matrix
of the observations. It is rare for this to be known. However, when it is, the expectation value of U is one, which means that the data are fitted within experimental error. Most often only the diagonal elements are known, in which case the objective function simplifies to
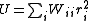
with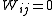
when j≠ i. Unit weights, 
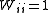, are often used but, in that case, the expectation value of U is the root mean square
of the experimental errors.
The minimization may be performed using the Gauss–Newton method. Firstly the objective function is linearised by approximating it as a first-order Taylor series
expansion about an initial parameter set, p.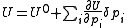
The increments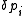
are to be added to the corresponding initial parameters such that U is less than U0. At the minimum the derivatives 
, which are simply related to the elements of the Jacobian matrix, J
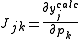
where pk is the kth parameter of the refinement, are equal to zero. One or more equilibrium constants may be parameters of the refinement. However, the measured quantities (see above) represented by y are not expressed in terms of the equilibrium constants, but in terms of the species concentrations, which are implicit functions of these parameters. Therefore the Jacobian elements must be obtained using implicit differentiation.
The parameter increments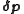
are calculated by solving the normal equations, derived from the conditions that 
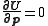at the minimum.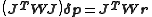
The increments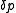
are added iteratively to the parameters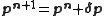
where n is an iteration number. The species concentrations and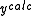
values are recalculated at every data point. The iterations are continued until no significant reduction in U is achieved, that is, until a convergence criterion is satisfied. If, however, the updated parameters do not result in a decrease of the objective function, that is, if divergence occurs, the increment calculation must be modified. The simplest modification is to use a fraction, f, of calculated increment, so-called shift-cutting.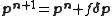
In this case, the direction of the shift vector,
, is unchanged. With the more powerful Levenberg–Marquardt algorithm, on the other hand, the shift vector is rotated towards the direction of steepest descent, by modifying the normal equations,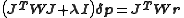
where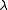
is the Marquardt parameter and I is an identity matrix. Other methods of handling divergence have been proposed.
A particular issue arises with NMR and spectrophotometric data. For the latter, the observed quantity is absorbance, A, and the Beer–Lambert law can be written as
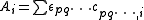
It can be seen that absorbance, A, is a linear function of the molar absorbptivities,
, at the path length used. In matrix notation
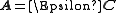
There are two approaches to the calculation of the unknown molar absorptivities
Therefore the parameter values are (approximately) linear combinations of the observed data values and the errors on the parameters, p, can be obtained by error propagation from the observations, yobs, using the linear formula. Let the variance-covariance matrix for the observations be denoted by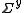
and that of the parameters by 
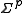. Then,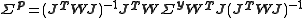
When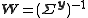
, this simplifies to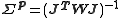
In most cases the errors on the observations are un-correlated, so that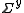
is diagonal
.
If so, each weight should be the reciprocal
of the variance of the corresponding observation. For example, in a potentiometric titration
, the weight at a titration point, k, can be given by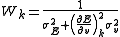
where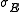
is the error in electrode potential or pH, 
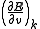is the slope of the titration curve
and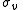
is the error on added volume.
When unit weights are used (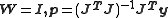
) it is implied that the experimental errors are uncorrelated and all equal: 
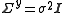, where 
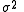is known as the variance of an observation of unit weight, and 
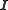is an identity matrix
. In this case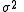
is approximated by 
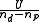, where U is the minimum value of the objective function and nd and np are the number of data and parameters, respectively.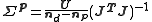
In all cases, the variance
of the parameter pi is given by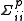
and the covariance between parameters pi and pj is given by 
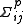. Standard deviation
is the square root of variance. These error estimates reflect only random errors in the measurements. The true uncertainty in the parameters is larger due to the presence of systematic errors which, by definition, cannot be quantified.
Note that even though the observations may be un-correlated, the parameters are always correlated.
.
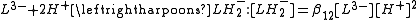
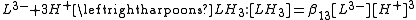
The stepwise association constant for formation of LH3 is given by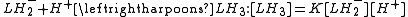
Substitute the expressions for the concentrations of LH3 and LH2− into this equation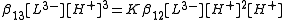
whence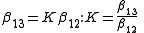
and since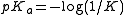
its value is given by
When calculating the error on the stepwise constant, the fact that the cumulative constants are correlated must be taken into account. By error propagation
and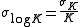
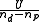is 1. It is therefore very useful to estimate experimental errors and derive some reasonable weights from them as this is an absolute indicator of the goodness of fit.
When unit weights are used, it is implied that all observations have the same variance.
, is expected to be equal to that variance.
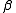should not be much larger than 0.01. In exploratory work where the nature of the species present is not known in advance, several different chemical models may be tested and compared. There will be models where the uncertainties in the best estimate of an equilibrium constant may be somewhat or even significantly larger than 
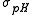, especially with those constants governing the formation of comparatively minor species, but the decision as to how large is acceptable remains subjective. The decision process as to whether or not to include comparatively uncertain equilibria in a model, and for the comparison of competing models in general, can be made objective and has been outlined by Hamilton.
At the minimum in U the system can be approximated to a linear one, the residuals in the case of unit weights are related to the observations by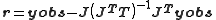
The symmetric, idempotent matrix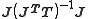
is known in the statistics literature as the hat matrix
, :
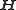. Thus,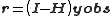
and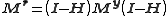
where I is an identity matrix
and Mr and My are the variance-covariance matrices of the residuals and observations, respectively. This shows that even though the observations may be un-correlated, the residuals are always correlated.
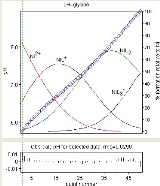
The diagram at the right shows the result of a refinement of the stability constants of Ni
Gly+, Ni(Gly)2 and Ni(Gly)3− (GlyH = glycine
). The observed values are shown a blue diamonds and the species concentrations, as a percentage of the total nickel, are superimposed. The residuals are shown in the lower box. The presence of correlation is evident in the way sequences all have the same sign. Correlation notwithstanding, the magnitudes of the residuals show some randomness. Individual residuals are mostly commensurate with experimental error (about 0.002 in pH). This is about as good as it gets.
With spectrophotometric data the molar absorptivity (or emissivity) values should all be positive. Most computer programs do not impose this constraint on the calculations.
.
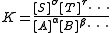
it is implied that the activity
Activity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
quotient is constant. In order for this assumption to be valid equilibrium constants should be determined in a medium of relatively high ionic strength
Ionic strength
The ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
. Where this is not possible, consideration should be given to possible activity variation.
The equilibrium expression above is a function of the concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
s [A], [B] etc. of the chemical species in equilibrium. The equilibrium constant value can be determined if any one of these concentrations can be measured. The general procedure is that the concentration in question is measured for a series of solutions with known analytical concentrations of the reactants. Typically, a titration
Titration
Titration, also known as titrimetry, is a common laboratory method of quantitative chemical analysis that is used to determine the unknown concentration of an identified analyte. Because volume measurements play a key role in titration, it is also known as volumetric analysis. A reagent, called the...
is performed with one or more reactants in the titration vessel and one or more reactants in the burette. Knowing the analytical concentrations of reactants initially in the reaction vessel and in the burette, all analytical concentrations can be derived as a function of the volume (or mass) of titrant added.
The equilibrium constants may be derived by best-fitting of the experimental data with a chemical model of the equilibrium system.
Experimental methods
There are four main experimental methods. For less commonly used methods, see Rossotti and Rossotti.Potentiometric measurements
A free concentration [A] or activity {A} is measured by means of an ion selective electrodeIon selective electrode
An ion-selective electrode , also known as a specific ion electrode , is a transducer that converts the activity of a specific ion dissolved in a solution into an electrical potential, which can be measured by a voltmeter or pH meter. The voltage is theoretically dependent on the logarithm of the...
such as the glass electrode
Glass electrode
A glass electrode is a type of ion-selective electrode made of a doped glass membrane that is sensitive to a specific ion. It is an important part of the instrumentation for chemical analysis and physico-chemical studies. In modern practice, widely used membranous ion-selective electrodes are part...
. If the electrode is calibrated using activity standards it is assumed that the Nernst equation
Nernst equation
In electrochemistry, the Nernst equation is an equation that can be used to determine the equilibrium reduction potential of a half-cell in an electrochemical cell. It can also be used to determine the total voltage for a full electrochemical cell...
applies in the form
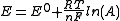
where E0 is the standard electrode potential
Standard electrode potential
In electrochemistry, the standard electrode potential, abbreviated E° or E , is the measure of individual potential of a reversible electrode at standard state, which is with solutes at an effective concentration of 1 mol dm−3, and gases at a pressure of 1 atm...
. When buffer
Buffer solution
A buffer solution is an aqueous solution consisting of a mixture of a weak acid and its conjugate base or a weak base and its conjugate acid. It has the property that the pH of the solution changes very little when a small amount of strong acid or base is added to it. Buffer solutions are used as a...
solutions of known pH are used for calibration the meter
PH meter
A pH meter is an electronic instrument used for measuring the pH of a liquid...
reading will be pH.
At 298K, 1 pH unit is approximately equal to 59 mV.
When the electrode is calibrated with solutions of known concentration, by means of a strong acid/strong base titration, for example, a modified Nernst equation is assumed.
- E = E0 + s log10[A]
s an empirical slope factor. A solution of known hydrogen ion concentration may be prepared by standardization of a strong acid
Strong acid
A strong acid is an acid that ionizes completely in an aqueous solution by losing one proton, according to the equationFor sulfuric acid which is diprotic, the "strong acid" designation refers only to dissociation of the first protonMore precisely, the acid must be stronger in aqueous solution than...
against borax
Borax
Borax, also known as sodium borate, sodium tetraborate, or disodium tetraborate, is an important boron compound, a mineral, and a salt of boric acid. It is usually a white powder consisting of soft colorless crystals that dissolve easily in water.Borax has a wide variety of uses...
. Constant-boiling
Azeotrope
An azeotrope is a mixture of two or more liquids in such a ratio that its composition cannot be changed by simple distillation. This occurs because, when an azeotrope is boiled, the resulting vapor has the same ratio of constituents as the original mixture....
hydrochloric acid
Hydrochloric acid
Hydrochloric acid is a solution of hydrogen chloride in water, that is a highly corrosive, strong mineral acid with many industrial uses. It is found naturally in gastric acid....
may also be used as a primary standard for hydrogen ion concentration.
Absorbance
It is assumed that the Beer–Lambert law applies.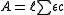where
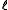is the optical path length, is a molar absorbance at unit path length and c is a concentration. More than one of the species may contribute to the absorbance. In principle absorbance may be measured at one wavelength only, but in present-day practice it is common to record complete spectra.Fluorescence (luminescence) intensity
It is assumed that the scattered light intensity is a linear function of species’ concentrations.where
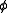is a proportionality constant.NMR chemical shift measurements
Chemical exchange is assumed to be rapid on the NMR time-scale. An individual chemical shift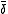 is the mole-fraction-weighted average of the shifts 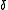of nuclei in contributing species.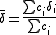Calorimetric measurements
Simultaneous measurement of K andH for 1:1 adducts is routinely carried out using Isothermal Titration CalorimetryIsothermal Titration Calorimetry
Isothermal titration calorimetry is a physical technique used to determine the thermodynamic parameters of interactions in solution. It is most often used to study the binding of small molecules to larger macromolecules .-Thermodynamic measurements:ITC is a quantitative technique that can...
. Extension to more complex systems is limited by the availability of suitable software.
Range and limitations
- Potentiometry. The most widely used electrode is the glass electrode which is selective for the hydrogen ion. This is suitable for all acid-base equilibria. Log10
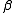values between about 2 and 11 can be measured directly by potentiometric titration using a glass electrode. This enormous range is possible because of the logarithmic response of the electrode. The limitations arise because the Nernst equation breaks down at very low or very high pH. The range can be extended by using the competition method. An example of the application of this method can be found in Palladium(II) cyanidePalladium(II) cyanidePalladium cyanides are chemical species with the empirical formula Pdn-. The dicyanide is a coordination polymer which was the first pure palladium compound isolated. In his attempts to produce pure platinum metal in 1804, W.H... - Absorbance and Luminescence. An upper limit on log10
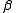of 4 is usually quoted, corresponding to the precision of the measurements, but it also depends on how intense the effect is. Spectra of contributing species should be clearly distinct from each other - NMR. Limited precision of chemical shift measurements also puts an upper limit of about 4 on log10
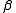. Limited to diamagnetic systems. - Calorimetry. Insufficient evidence is currently available.
Computational methods
It is assumed that the experimental data which have been collected comprise a set of data points. At each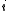-th data point, the analytical concentrations of the reactants, 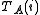, 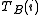etc. are known along with a measured quantity, , that depends on one or more of these analytical concentrations. A general computational procedure has three main components.
- Definion of a chemical model of the equilibria
- Calculation of the concentrations of all the chemical species in each solution
- Refinement of the equilibrium constants
- Model selection
The chemical model
The chemical model consists of a set of chemical species present in solution, both the reactants added to the reaction mixture and the complex species formed from them. Denoting the reactants by A, B ..., each complex species is specified by the stoichiometric coefficients that relate the particular combination of reactants forming them.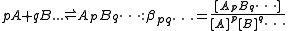When using general-purpose computer programs, it is usual to use cumulative, association constants, as shown above. Electrical charges are not shown in general expressions such as this and are often omitted from specific expressions, for simplicity of notation. In fact, electrical charges have no bearing on the equilibrium processes other that there being a requirement for overall electrical neutrality in all systems.
With aqueous solutions the concentrations of proton (hydronium ion) and hydroxide ion are constrained by the self-dissociation of water.
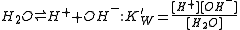
With dilute solutions the concentration of water can be assumed to be constant so the equilibrium expression is written in the familiar form of the ionic product
Self-ionization of water
The self-ionization of water is the chemical reaction in which a proton is transferred from one water molecule to another, in pure water or an aqueous solution, to create the two ions, hydronium, H3O+ and hydroxide, OH−...
of water.
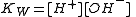
When both H+ and OH− must be considered as reactants, one of them is eliminated from the model by specifying that its concentration is to be derived from the concentration of the other. Usually the concentration of the hydroxide ion is given by
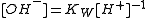
In this case the equilibrium constant for the formation of hydroxide has the stoichiometric coefficients −1 in regard to the proton and zero for the other reactants. This has important implications for all protonation equilibria in aqueous solution and for hydrolysis constants in particular.
It is quite usual to omit from the model those species whose concentrations are considered to be negligible. For example it is usually assumed then there is no interaction between the reactants and/or complexes and the electrolyte used to maintain constant ionic strength or the buffer used to maintain constant pH. These assumptions may or may not be justified. Also, it is implicitly assumed that there are no other complex species present. When complexes are wrongly ignored a systematic error
Systematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
is introduced into the calculations.
Equilibrium constant values are usually estimated initially by reference to data sources.
Speciation calculations
A speciation calculation is one in which the concentrations of all the species in an equilibrium system are calculated, knowing the analytical concentrations, TA, TB etc. of the reactants A, B etc. This means solving a set of non-linear equations of mass-balance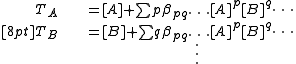for the free concentrations [A], [B] etc. The concentrations of the complexes are derived from the free concentrations via the chemical model. Some authors include the free reactant terms in the sums by declaring identity (unit)
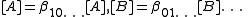
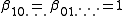
constants for which the stoichiometric coefficients are 1 for the reactant concerned and zero for all other reactants:In this manner, all chemical species, including the free reactants, are treated in the same way, having been formed from the combination of reactants that is specified by the stoichiometric coefficients. The mass-balance equations assume the simpler form.
In a titration system the analytical concentrations of the reactants at each titration point are obtained from the initial conditions, the burette concentrations and volumes. The analytical (total) concentration of a reactant R at the ith titration point is given by
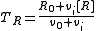
where
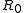is the initial amount of R in the titration vessel, 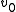is the initial volume, 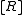is the concentration of R in the burette and 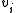is the volume added. The burette concentration of a reactant not present in the burette is taken to be zero.In general, solving these non-linear equations presents a formidable challenge because of the huge range over which the free concentrations may vary. At the beginning, values for the free concentrations must be estimated. Then, these values are refined, usually by means of Newton–Raphson
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
iterations. The logarithms of the free concentrations may be refined rather than the free concentrations themselves. Refinement of the logarithms of the free concentrations has the added advantage of automatically imposing a non-negativity constraint on the free concentrations. Once the free reactant concentrations have been calculated, the concentrations of the complexes are derived from them and the equilibrium constants.
Note that the free reactant concentrations can be regarded as implicit parameters in the equilibrium constant refinement process. In that context the values of the free concentrations are constrained by forcing the conditions of mass-balance to apply at all stages of the process.
Equilibrium constant refinement
The objective of the refinement process it to find equilibrium constant values that give the best fit to the experimental data. This is usually achieved by minimising an objective function, U, by the method of non-linear least-squares. First the residuals are defined as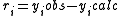Then the most general objective function is given by
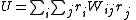
The matrix of weights, W, should be, ideally, the inverse of the variance-covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the observations. It is rare for this to be known. However, when it is, the expectation value of U is one, which means that the data are fitted within experimental error. Most often only the diagonal elements are known, in which case the objective function simplifies to
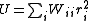
with
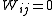when j≠ i. Unit weights, 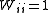, are often used but, in that case, the expectation value of U is the root mean squareRoot mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
of the experimental errors.
The minimization may be performed using the Gauss–Newton method. Firstly the objective function is linearised by approximating it as a first-order Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion about an initial parameter set, p.
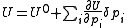
The increments
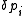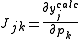
are to be added to the corresponding initial parameters such that U is less than U0. At the minimum the derivatives , which are simply related to the elements of the Jacobian matrix, Jwhere pk is the kth parameter of the refinement, are equal to zero. One or more equilibrium constants may be parameters of the refinement. However, the measured quantities (see above) represented by y are not expressed in terms of the equilibrium constants, but in terms of the species concentrations, which are implicit functions of these parameters. Therefore the Jacobian elements must be obtained using implicit differentiation.
The parameter increments
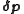are calculated by solving the normal equations, derived from the conditions that 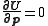at the minimum.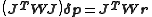The increments
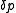are added iteratively to the parameters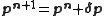where n is an iteration number. The species concentrations and
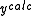values are recalculated at every data point. The iterations are continued until no significant reduction in U is achieved, that is, until a convergence criterion is satisfied. If, however, the updated parameters do not result in a decrease of the objective function, that is, if divergence occurs, the increment calculation must be modified. The simplest modification is to use a fraction, f, of calculated increment, so-called shift-cutting.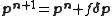In this case, the direction of the shift vector,
, is unchanged. With the more powerful Levenberg–Marquardt algorithm, on the other hand, the shift vector is rotated towards the direction of steepest descent, by modifying the normal equations,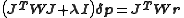where
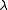is the Marquardt parameter and I is an identity matrix. Other methods of handling divergence have been proposed.A particular issue arises with NMR and spectrophotometric data. For the latter, the observed quantity is absorbance, A, and the Beer–Lambert law can be written as
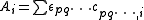
It can be seen that absorbance, A, is a linear function of the molar absorbptivities,
, at the path length used. In matrix notation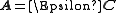There are two approaches to the calculation of the unknown molar absorptivities
- 1) The
values are considered to be parameters of the minimization and the Jacobian is constructed on that basis. However, the 
values themselves are calculated at each step of the refinement by linear least-squares:
- using the refined values of the equilibrium constants to obtain the speciation. The matrix
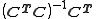is an example of a pseudo-inverse. - 2) The Beer–Lambert law is written as
- Golub and Pereyra showed how the pseudo-inverse can be differentiated so that parameter increments for both molar absorptivities and equilibrium constants can be calculated by solving the normal equations.
Parameter errors and correlation
In the region close to the minimum of the objective function, U, the system approximates to a linear least-squares system, for whichTherefore the parameter values are (approximately) linear combinations of the observed data values and the errors on the parameters, p, can be obtained by error propagation from the observations, yobs, using the linear formula. Let the variance-covariance matrix for the observations be denoted by
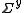and that of the parameters by 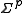. Then,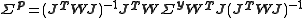When
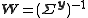, this simplifies to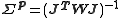In most cases the errors on the observations are un-correlated, so that
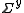is diagonalDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
.
If so, each weight should be the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the variance of the corresponding observation. For example, in a potentiometric titration
Potentiometric titration
Potentiometric titration is a technique similar to direct titration of a redox reaction. No indicator is used, instead the voltage across the analyte, typically an electrolyte solution is measured. To do this, two electrodes are used, a neutral electrode and a standard reference electrode. The...
, the weight at a titration point, k, can be given by
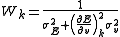
where
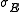is the error in electrode potential or pH, 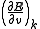is the slope of the titration curveTitration curve
Titrations are often recorded on titration curves, whose compositions are generally identical: the independent variable is the volume of the titrant, while the dependent variable is the pH of the solution...
and
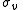is the error on added volume.When unit weights are used (
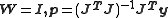) it is implied that the experimental errors are uncorrelated and all equal: 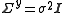, where 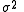is known as the variance of an observation of unit weight, and 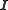is an identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In this case
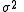is approximated by 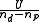, where U is the minimum value of the objective function and nd and np are the number of data and parameters, respectively.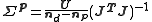In all cases, the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the parameter pi is given by
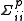and the covariance between parameters pi and pj is given by 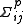. Standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
is the square root of variance. These error estimates reflect only random errors in the measurements. The true uncertainty in the parameters is larger due to the presence of systematic errors which, by definition, cannot be quantified.
Note that even though the observations may be un-correlated, the parameters are always correlated.
Derived constants
When cumulative constants have been refined it is often useful to derive stepwise constants from them. The general procedure is to write down the defining expressions for all the constants involved and then to equate concentrations. For example, suppose that one wishes to derive the pKa for removing one proton from a tribasic acid, LH3, such as citric acidCitric acid
Citric acid is a weak organic acid. It is a natural preservative/conservative and is also used to add an acidic, or sour, taste to foods and soft drinks...
.
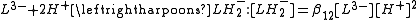
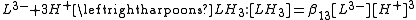
The stepwise association constant for formation of LH3 is given by
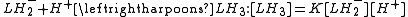
Substitute the expressions for the concentrations of LH3 and LH2− into this equation
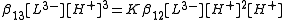
whence
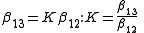
and since
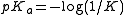its value is given byWhen calculating the error on the stepwise constant, the fact that the cumulative constants are correlated must be taken into account. By error propagation
and
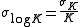
Model selection
Once a refinement has been completed the results should be checked to verify that the chosen model is acceptable. generally speaking, a model is acceptable when the data are fitted within experimental error, but there is no single criterion with which to make the judgement. The following should be taken into consideration.The objective function
When the weights have been correctly derived from estimates of experimental error, the expectation value of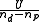 is 1. It is therefore very useful to estimate experimental errors and derive some reasonable weights from them as this is an absolute indicator of the goodness of fit.When unit weights are used, it is implied that all observations have the same variance.
, is expected to be equal to that variance.Parameter errors
One would want the errors on the stability constants to be roughly commensurate with experimental error. For example, with pH titration data, if pH is measured to 2 decimal places, the errors of log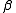 should not be much larger than 0.01. In exploratory work where the nature of the species present is not known in advance, several different chemical models may be tested and compared. There will be models where the uncertainties in the best estimate of an equilibrium constant may be somewhat or even significantly larger than 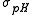, especially with those constants governing the formation of comparatively minor species, but the decision as to how large is acceptable remains subjective. The decision process as to whether or not to include comparatively uncertain equilibria in a model, and for the comparison of competing models in general, can be made objective and has been outlined by Hamilton.Distribution of residuals
At the minimum in U the system can be approximated to a linear one, the residuals in the case of unit weights are related to the observations by
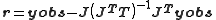
The symmetric, idempotent matrix
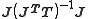is known in the statistics literature as the hat matrixHat matrix
In statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...
, :
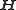. Thus,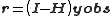and
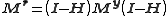
where I is an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and Mr and My are the variance-covariance matrices of the residuals and observations, respectively. This shows that even though the observations may be un-correlated, the residuals are always correlated.
The diagram at the right shows the result of a refinement of the stability constants of Ni
Nickel
Nickel is a chemical element with the chemical symbol Ni and atomic number 28. It is a silvery-white lustrous metal with a slight golden tinge. Nickel belongs to the transition metals and is hard and ductile...
Gly+, Ni(Gly)2 and Ni(Gly)3− (GlyH = glycine
Glycine
Glycine is an organic compound with the formula NH2CH2COOH. Having a hydrogen substituent as its 'side chain', glycine is the smallest of the 20 amino acids commonly found in proteins. Its codons are GGU, GGC, GGA, GGG cf. the genetic code.Glycine is a colourless, sweet-tasting crystalline solid...
). The observed values are shown a blue diamonds and the species concentrations, as a percentage of the total nickel, are superimposed. The residuals are shown in the lower box. The presence of correlation is evident in the way sequences all have the same sign. Correlation notwithstanding, the magnitudes of the residuals show some randomness. Individual residuals are mostly commensurate with experimental error (about 0.002 in pH). This is about as good as it gets.
Physical constraints
Some physical constraints are usually incorporated in the calculations. For example, all the concentrations of free reactants and species must have positive values and association constants must have positive values.With spectrophotometric data the molar absorptivity (or emissivity) values should all be positive. Most computer programs do not impose this constraint on the calculations.
Other models
If the model is not acceptable a variety of other models should be examined in order to find the model that best fits the experimental data, within experimental error. The main difficulty is with the so-called minor species. These are species whose concentration is so low that the effect on the measured quantity is at or below the level of error in the experimental measurement. The constant for a minor species may prove impossible to determine if there is no means to increase the concentration of the species..