
Divide-and-conquer eigenvalue algorithm
Encyclopedia
Divide-and-conquer eigenvalue algorithms are a class of eigenvalue algorithm
s for Hermitian or real
symmetric matrices that have recently (circa 1990s) become competitive in terms of stability
and efficiency
with more traditional algorithms such as the QR algorithm
. The basic concept behind these algorithms is the divide-and-conquer
approach from computer science
. An eigenvalue problem is divided into two problems of roughly half the size, each of these are solved recursively
, and the eigenvalues of the original problem are computed from the results of these smaller problems.
Here we present the simplest version of a divide-and-conquer algorithm, similar to the one originally proposed by Cuppen in 1981. Many details that lie outside the scope of this article will be omitted; however, without considering these details, the algorithm is not fully stable.
 matrix, the standard method for this, via Householder reflections, takes
matrix, the standard method for this, via Householder reflections, takes 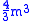 flops
flops
, or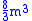 if eigenvectors are needed as well. There are other algorithms, such as the Arnoldi iteration
if eigenvectors are needed as well. There are other algorithms, such as the Arnoldi iteration
, which may do better for certain classes of matrices; we will not consider this further here.
In certain cases, it is possible to deflate an eigenvalue problem into smaller problems. Consider a block diagonal matrix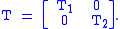
The eigenvalues and eigenvectors of are simply those of
are simply those of 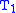 and
and 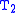 , and it will almost always be faster to solve these two smaller problems than to solve the original problem all at once. This technique can be used to improve the efficiency of many eigenvalue algorithms, but it has special significance to divide-and-conquer.
, and it will almost always be faster to solve these two smaller problems than to solve the original problem all at once. This technique can be used to improve the efficiency of many eigenvalue algorithms, but it has special significance to divide-and-conquer.
For the rest of this article, we will assume the input to the divide-and-conquer algorithm is an real symmetric tridiagonal matrix
real symmetric tridiagonal matrix  . Although the algorithm can be modified for Hermitian matrices, we do not give the details here.
. Although the algorithm can be modified for Hermitian matrices, we do not give the details here.
The size of submatrix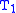 we will call
we will call  , and then
, and then 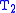 is
is 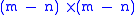 . Note that the remark about
. Note that the remark about  being almost block diagonal is true regardless of how
being almost block diagonal is true regardless of how  is chosen (i.e., there are many ways to so decompose the matrix). However, it makes sense, from an efficiency standpoint, to choose
is chosen (i.e., there are many ways to so decompose the matrix). However, it makes sense, from an efficiency standpoint, to choose 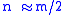 .
.
We write as a block diagonal matrix, plus a rank-1
as a block diagonal matrix, plus a rank-1
correction:
The only difference between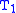 and
and 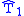 is that the lower right entry
is that the lower right entry  in
in 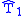 has been replaced with
has been replaced with  and similarly, in
and similarly, in 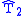 the top left entry
the top left entry 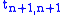 has been replaced with
has been replaced with 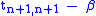 .
.
The remainder of the divide step is to solve for the eigenvalues (and if desired the eigenvectors) of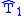 and
and 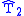 , that is to find the diagonalization
, that is to find the diagonalization
s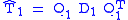 and
and 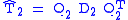 . This can be accomplished with recursive calls to the divide-and-conquer algorithm, although practical implementations often switch to the QR algorithm for small enough submatrices.
. This can be accomplished with recursive calls to the divide-and-conquer algorithm, although practical implementations often switch to the QR algorithm for small enough submatrices.
First, define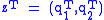 , where
, where 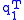 is the last row of
is the last row of  and
and 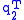 is the first row of
is the first row of 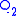 . It is now elementary to show that
. It is now elementary to show that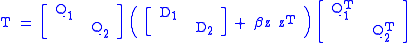
The remaining task has been reduced to finding the eigenvalues of a diagonal matrix plus a rank-one correction. Before showing how to do this, let us simplify the notation. We are looking for the eigenvalues of the matrix , where
, where  is diagonal with distinct entries and
is diagonal with distinct entries and  is any vector with nonzero entries.
is any vector with nonzero entries.
If wi is zero, (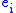 ,di) is an eigenpair of
,di) is an eigenpair of  since
since
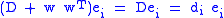 .
.
If is an eigenvalue, we have:
is an eigenvalue, we have: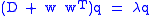
where is the corresponding eigenvector. Now
is the corresponding eigenvector. Now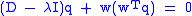
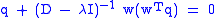
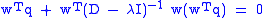
Keep in mind that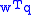 is a nonzero scalar. Neither
is a nonzero scalar. Neither  nor
nor  are zero. If
are zero. If 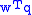 were to be zero,
were to be zero,  would be an eigenvector of
would be an eigenvector of  by
by 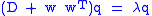 . If that were the case,
. If that were the case,  would contain only one nonzero position since
would contain only one nonzero position since  is distinct diagonal and thus the inner product
is distinct diagonal and thus the inner product 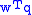 can not be zero after all. Therefore, we have:
can not be zero after all. Therefore, we have: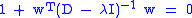
or written as a scalar equation,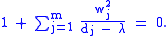
This equation is known as the secular equation. The problem has therefore been reduced to finding the roots of the rational function
defined by the left-hand side of this equation.
All general eigenvalue algorithms must be iterative, and the divide-and-conquer algorithm is no different. Solving the nonlinear secular equation requires an iterative technique, such as the Newton–Raphson method
. However, each root can be found in O
(1) iterations, each of which requires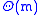 flops (for an
flops (for an  -degree rational function), making the cost of the iterative part of this algorithm
-degree rational function), making the cost of the iterative part of this algorithm  .
.
to analyze the running time. Remember that above we stated we choose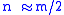 . We can write the recurrence relation
. We can write the recurrence relation
: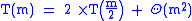
In the notation of the Master theorem, and thus
and thus 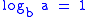 . Clearly,
. Clearly,  , so we have
, so we have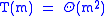
Remember that above we pointed out that reducing a Hermitian matrix to tridiagonal form takes flops. This dwarfs the running time of the divide-and-conquer part, and at this point it is not clear what advantage the divide-and-conquer algorithm offers over the QR algorithm (which also takes
flops. This dwarfs the running time of the divide-and-conquer part, and at this point it is not clear what advantage the divide-and-conquer algorithm offers over the QR algorithm (which also takes 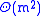 flops for tridiagonal matrices).
flops for tridiagonal matrices).
The advantage of divide-and-conquer comes when eigenvectors are needed as well. If this is the case, reduction to tridiagonal form takes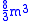 , but the second part of the algorithm takes
, but the second part of the algorithm takes 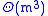 as well. For the QR algorithm with a reasonable target precision, this is
as well. For the QR algorithm with a reasonable target precision, this is  , whereas for divide-and-conquer it is
, whereas for divide-and-conquer it is 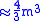 . The reason for this improvement is that in divide-and-conquer, the
. The reason for this improvement is that in divide-and-conquer, the 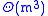 part of the algorithm (multiplying
part of the algorithm (multiplying  matrices) is separate from the iteration, whereas in QR, this must occur in every iterative step. Adding the
matrices) is separate from the iteration, whereas in QR, this must occur in every iterative step. Adding the 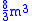 flops for the reduction, the total improvement is from
flops for the reduction, the total improvement is from 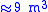 to
to  flops.
flops.
Practical use of the divide-and-conquer algorithm has shown that in most realistic eigenvalue problems, the algorithm actually does better than this. The reason is that very often the matrices and the vectors
and the vectors  tend to be numerically sparse, meaning that they have many entries with values smaller than the floating point
tend to be numerically sparse, meaning that they have many entries with values smaller than the floating point
precision, allowing for numerical deflation, i.e. breaking the problem into uncoupled subproblems.
There exist specialized root-finding techniques for rational functions that may do better than the Newton-Raphson method in terms of both performance and stability. These can be used to improve the iterative part of the divide-and-conquer algorithm.
The divide-and-conquer algorithm is readily parallelized
, and linear algebra
computing packages such as LAPACK
contain high-quality parallel implementations.
Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s for Hermitian or real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
symmetric matrices that have recently (circa 1990s) become competitive in terms of stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
and efficiency
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
with more traditional algorithms such as the QR algorithm
QR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
. The basic concept behind these algorithms is the divide-and-conquer
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
approach from computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. An eigenvalue problem is divided into two problems of roughly half the size, each of these are solved recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, and the eigenvalues of the original problem are computed from the results of these smaller problems.
Here we present the simplest version of a divide-and-conquer algorithm, similar to the one originally proposed by Cuppen in 1981. Many details that lie outside the scope of this article will be omitted; however, without considering these details, the algorithm is not fully stable.
Background
As with most eigenvalue algorithms for Hermitian matrices, divide-and-conquer begins with a reduction to tridiagonal form. For an matrix, the standard method for this, via Householder reflections, takes
matrix, the standard method for this, via Householder reflections, takes 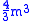 flops
flopsFLOPS
In computing, FLOPS is a measure of a computer's performance, especially in fields of scientific calculations that make heavy use of floating-point calculations, similar to the older, simpler, instructions per second...
, or
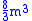 if eigenvectors are needed as well. There are other algorithms, such as the Arnoldi iteration
if eigenvectors are needed as well. There are other algorithms, such as the Arnoldi iterationArnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
, which may do better for certain classes of matrices; we will not consider this further here.
In certain cases, it is possible to deflate an eigenvalue problem into smaller problems. Consider a block diagonal matrix
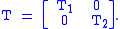
The eigenvalues and eigenvectors of
 are simply those of
are simply those of 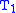 and
and 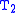 , and it will almost always be faster to solve these two smaller problems than to solve the original problem all at once. This technique can be used to improve the efficiency of many eigenvalue algorithms, but it has special significance to divide-and-conquer.
, and it will almost always be faster to solve these two smaller problems than to solve the original problem all at once. This technique can be used to improve the efficiency of many eigenvalue algorithms, but it has special significance to divide-and-conquer.For the rest of this article, we will assume the input to the divide-and-conquer algorithm is an
 real symmetric tridiagonal matrix
real symmetric tridiagonal matrix  . Although the algorithm can be modified for Hermitian matrices, we do not give the details here.
. Although the algorithm can be modified for Hermitian matrices, we do not give the details here.Divide
The divide part of the divide-and-conquer algorithm comes from the realization that a tridiagonal matrix is "almost" block diagonal.The size of submatrix
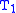 we will call
we will call  , and then
, and then 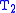 is
is 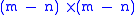 . Note that the remark about
. Note that the remark about  being almost block diagonal is true regardless of how
being almost block diagonal is true regardless of how  is chosen (i.e., there are many ways to so decompose the matrix). However, it makes sense, from an efficiency standpoint, to choose
is chosen (i.e., there are many ways to so decompose the matrix). However, it makes sense, from an efficiency standpoint, to choose 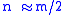 .
.We write
 as a block diagonal matrix, plus a rank-1
as a block diagonal matrix, plus a rank-1Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
correction:
The only difference between
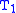 and
and 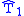 is that the lower right entry
is that the lower right entry  in
in 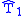 has been replaced with
has been replaced with  and similarly, in
and similarly, in 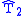 the top left entry
the top left entry 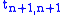 has been replaced with
has been replaced with 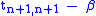 .
.The remainder of the divide step is to solve for the eigenvalues (and if desired the eigenvectors) of
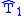 and
and 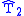 , that is to find the diagonalization
, that is to find the diagonalizationDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
s
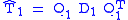 and
and 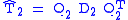 . This can be accomplished with recursive calls to the divide-and-conquer algorithm, although practical implementations often switch to the QR algorithm for small enough submatrices.
. This can be accomplished with recursive calls to the divide-and-conquer algorithm, although practical implementations often switch to the QR algorithm for small enough submatrices.Conquer
The conquer part of the algorithm is the unintuitive part. Given the diagonalizations of the submatrices, calculated above, how do we find the diagonalization of the original matrix?First, define
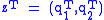 , where
, where 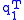 is the last row of
is the last row of  and
and 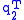 is the first row of
is the first row of 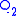 . It is now elementary to show that
. It is now elementary to show that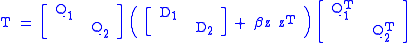
The remaining task has been reduced to finding the eigenvalues of a diagonal matrix plus a rank-one correction. Before showing how to do this, let us simplify the notation. We are looking for the eigenvalues of the matrix
 , where
, where  is diagonal with distinct entries and
is diagonal with distinct entries and  is any vector with nonzero entries.
is any vector with nonzero entries.If wi is zero, (
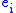 ,di) is an eigenpair of
,di) is an eigenpair of  since
since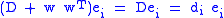 .
.If
 is an eigenvalue, we have:
is an eigenvalue, we have: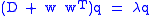
where
 is the corresponding eigenvector. Now
is the corresponding eigenvector. Now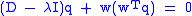
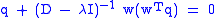
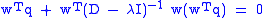
Keep in mind that
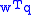 is a nonzero scalar. Neither
is a nonzero scalar. Neither  nor
nor  are zero. If
are zero. If 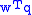 were to be zero,
were to be zero,  would be an eigenvector of
would be an eigenvector of  by
by 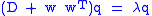 . If that were the case,
. If that were the case,  would contain only one nonzero position since
would contain only one nonzero position since  is distinct diagonal and thus the inner product
is distinct diagonal and thus the inner product 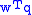 can not be zero after all. Therefore, we have:
can not be zero after all. Therefore, we have: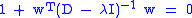
or written as a scalar equation,
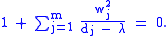
This equation is known as the secular equation. The problem has therefore been reduced to finding the roots of the rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
defined by the left-hand side of this equation.
All general eigenvalue algorithms must be iterative, and the divide-and-conquer algorithm is no different. Solving the nonlinear secular equation requires an iterative technique, such as the Newton–Raphson method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. However, each root can be found in O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(1) iterations, each of which requires
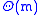 flops (for an
flops (for an  -degree rational function), making the cost of the iterative part of this algorithm
-degree rational function), making the cost of the iterative part of this algorithm  .
.Analysis
As is common for divide and conquer algorithms, we will use the Master theoremMaster theorem
In the analysis of algorithms, the master theorem provides a cookbook solution in asymptotic terms for recurrence relations of types that occur in the analysis of many divide and conquer algorithms...
to analyze the running time. Remember that above we stated we choose
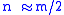 . We can write the recurrence relation
. We can write the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
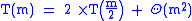
In the notation of the Master theorem,
 and thus
and thus 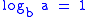 . Clearly,
. Clearly,  , so we have
, so we have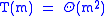
Remember that above we pointed out that reducing a Hermitian matrix to tridiagonal form takes
 flops. This dwarfs the running time of the divide-and-conquer part, and at this point it is not clear what advantage the divide-and-conquer algorithm offers over the QR algorithm (which also takes
flops. This dwarfs the running time of the divide-and-conquer part, and at this point it is not clear what advantage the divide-and-conquer algorithm offers over the QR algorithm (which also takes 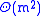 flops for tridiagonal matrices).
flops for tridiagonal matrices).The advantage of divide-and-conquer comes when eigenvectors are needed as well. If this is the case, reduction to tridiagonal form takes
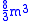 , but the second part of the algorithm takes
, but the second part of the algorithm takes 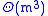 as well. For the QR algorithm with a reasonable target precision, this is
as well. For the QR algorithm with a reasonable target precision, this is  , whereas for divide-and-conquer it is
, whereas for divide-and-conquer it is 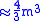 . The reason for this improvement is that in divide-and-conquer, the
. The reason for this improvement is that in divide-and-conquer, the 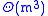 part of the algorithm (multiplying
part of the algorithm (multiplying  matrices) is separate from the iteration, whereas in QR, this must occur in every iterative step. Adding the
matrices) is separate from the iteration, whereas in QR, this must occur in every iterative step. Adding the 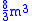 flops for the reduction, the total improvement is from
flops for the reduction, the total improvement is from 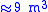 to
to  flops.
flops.Practical use of the divide-and-conquer algorithm has shown that in most realistic eigenvalue problems, the algorithm actually does better than this. The reason is that very often the matrices
 and the vectors
and the vectors  tend to be numerically sparse, meaning that they have many entries with values smaller than the floating point
tend to be numerically sparse, meaning that they have many entries with values smaller than the floating pointFloating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
precision, allowing for numerical deflation, i.e. breaking the problem into uncoupled subproblems.
Variants and implementation
The algorithm presented here is the simplest version. In many practical implementations, more complicated rank-1 corrections are used to guarantee stability; some variants even use rank-2 corrections.There exist specialized root-finding techniques for rational functions that may do better than the Newton-Raphson method in terms of both performance and stability. These can be used to improve the iterative part of the divide-and-conquer algorithm.
The divide-and-conquer algorithm is readily parallelized
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
, and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
computing packages such as LAPACK
LAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
contain high-quality parallel implementations.

