Ear decomposition
Encyclopedia
In graph theory
, an ear of an undirected graph G is a path
P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree
two in P. An ear decomposition of an undirected graph G is a partition
of its set of edges into a sequence of ears, such that the one or two endpoints of each ear belong to earlier ears in the sequence and such that the internal vertices of each ear do not belong to any earlier ear. Additionally, in most cases the first ear in the sequence must be a cycle. An open ear decomposition or a proper ear decomposition is an ear decomposition in which the two endpoints of each ear after the first are distinct from each other.
Ear decompositions may be used to characterize several important graph classes, and as part of efficient graph algorithms. They may also be generalized from graphs to matroid
s.
if the removal of any (k − 1) vertices leaves a connected subgraph, and k-edge-connected
if the removal of any (k − 1) edges leaves a connected subgraph.
The following result is due to :
The following result is due to :
Robbins introduced the ear decomposition of 2-edge-connected graphs as a tool for proving the Robbins theorem
, that these are exactly the graphs that may be given a strongly connected orientation. Because of the pioneering work of Whitney and Robbins on ear decompositions, an ear decomposition is sometimes also called a Whitney–Robbins synthesis .
s. An ear would then be a directed path where all internal vertices have indegree and outdegree equal to 1. A directed graph is strongly connected if it contains a directed path from every vertex to every other vertex. Then we have the following theorem:
is a graph with an odd number of vertices, such that for each vertex v, if v is removed from the graph then the remaining vertices have a perfect matching. found that:
More generally, a result of makes it possible to find in any graph G the ear decomposition with the fewest even ears.
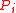, there is a single ear 
, 
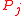, such that both endpoints of 
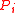lie on 
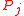. A nested ear decomposition is a tree ear decomposition such that, within each ear 
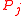, the set of pairs of endpoints of other ears 
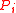that lie within 
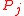form a set of nested intervals. A series-parallel graph
is a graph with two designated terminals s and t that can be formed recursively by combining smaller series-parallel graphs in one of two ways: series composition (identifying one terminal from one smaller graph with one terminal from the other smaller graph, and keeping the other two terminals as the terminals of the combined graph) and parallel composition (identifying both pairs of terminals from the two smaller graphs).
The following result is due to :
Moreover, any open ear decomposition of a 2-vertex-connected series-parallel graph must be nested. The result may be extended to series-parallel graphs that are not 2-vertex-connected by using open ear decompositions that start with a path between the two terminals.
s. An ear decomposition of a matroid is defined to be a sequence of circuits of the matroid, with two properties:
When applied to the graphic matroid of a graph G, this definition of an ear decomposition coincides with the definition of a proper ear decomposition of G: improper decompositions are excluded by the requirement that each circuit include at least one edge that also belongs to previous circuits. Using this definition, a matroid may be defined as factor-critical when it has an ear decomposition in which each circuit in the sequence has an odd number of new elements .
that finds each ear one at a time.
, , and provided efficient parallel algorithm
s for constructing ear decompositions of various types. For instance, to find an ear decomposition of a 2-edge-connected graph, the algorithm of proceeds according to the following steps:
These algorithms may be used as subroutines for other problems including testing connectivity, recognizing series-parallel graphs, and constructing st-numberings of graphs (an important subroutine in planarity testing
).
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an ear of an undirected graph G is a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
two in P. An ear decomposition of an undirected graph G is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of its set of edges into a sequence of ears, such that the one or two endpoints of each ear belong to earlier ears in the sequence and such that the internal vertices of each ear do not belong to any earlier ear. Additionally, in most cases the first ear in the sequence must be a cycle. An open ear decomposition or a proper ear decomposition is an ear decomposition in which the two endpoints of each ear after the first are distinct from each other.
Ear decompositions may be used to characterize several important graph classes, and as part of efficient graph algorithms. They may also be generalized from graphs to matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s.
Characterizing graph classes
Several important classes of graphs may be characterized as the graphs having certain types of ear decompositions.Graph connectivity
A graph is k-vertex-connectedK-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
if the removal of any (k − 1) vertices leaves a connected subgraph, and k-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
if the removal of any (k − 1) edges leaves a connected subgraph.
The following result is due to :
- A graph
with 
has a proper ear decomposition if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is 2-vertex-connectedK-vertex-connected graphIn graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
.
The following result is due to :
- A graph
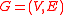has an ear decomposition if and only if 
is 2-edge-connectedK-edge-connected graphIn graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
.
Robbins introduced the ear decomposition of 2-edge-connected graphs as a tool for proving the Robbins theorem
Robbins theorem
In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs...
, that these are exactly the graphs that may be given a strongly connected orientation. Because of the pioneering work of Whitney and Robbins on ear decompositions, an ear decomposition is sometimes also called a Whitney–Robbins synthesis .
Strong connectivity of directed graphs
The above definitions can also be applied to directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s. An ear would then be a directed path where all internal vertices have indegree and outdegree equal to 1. A directed graph is strongly connected if it contains a directed path from every vertex to every other vertex. Then we have the following theorem:
- A directed graph
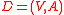is strongly connected if and only if 
has an ear decomposition.
Factor-critical graphs
An ear decomposition is odd if each of its ears uses an odd number of edges. A factor-critical graphFactor-critical graph
In graph theory, a mathematical discipline, a factor-critical graph is a graph with vertices in which every subgraph of vertices has a perfect matching, a subset of its edges such that each of the vertices is the endpoint of exactly one of the edges in the subset.A matching that covers all but...
is a graph with an odd number of vertices, such that for each vertex v, if v is removed from the graph then the remaining vertices have a perfect matching. found that:
- A graph G is factor-critical if and only if G has an odd ear decomposition.
More generally, a result of makes it possible to find in any graph G the ear decomposition with the fewest even ears.
Series-parallel graphs
A tree ear decomposition is a proper ear decomposition in which the first ear is a single edge and for each subsequent ear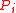, there is a single ear 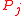, , such that both endpoints of 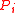lie on 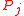. A nested ear decomposition is a tree ear decomposition such that, within each ear 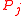, the set of pairs of endpoints of other ears 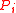that lie within 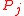form a set of nested intervals. A series-parallel graphSeries-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
is a graph with two designated terminals s and t that can be formed recursively by combining smaller series-parallel graphs in one of two ways: series composition (identifying one terminal from one smaller graph with one terminal from the other smaller graph, and keeping the other two terminals as the terminals of the combined graph) and parallel composition (identifying both pairs of terminals from the two smaller graphs).
The following result is due to :
- A 2-vertex-connected graph is series-parallel if and only if it has a nested ear decomposition.
Moreover, any open ear decomposition of a 2-vertex-connected series-parallel graph must be nested. The result may be extended to series-parallel graphs that are not 2-vertex-connected by using open ear decompositions that start with a path between the two terminals.
Matroids
The concept of an ear decomposition can be extended from graphs to matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s. An ear decomposition of a matroid is defined to be a sequence of circuits of the matroid, with two properties:
- each circuit in the sequence has a nonempty intersection with the previous circuits, and
- each circuit in the sequence remains a circuit even if all previous circuits in the sequence are contracted.
When applied to the graphic matroid of a graph G, this definition of an ear decomposition coincides with the definition of a proper ear decomposition of G: improper decompositions are excluded by the requirement that each circuit include at least one edge that also belongs to previous circuits. Using this definition, a matroid may be defined as factor-critical when it has an ear decomposition in which each circuit in the sequence has an odd number of new elements .
Algorithms
On classical computers, ear decompositions of 2-edge-connected graphs and open ear decompositions of 2-edge-connected graphs may be found by a greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
that finds each ear one at a time.
, , and provided efficient parallel algorithm
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
s for constructing ear decompositions of various types. For instance, to find an ear decomposition of a 2-edge-connected graph, the algorithm of proceeds according to the following steps:
- Find a spanning treeSpanning treeSpanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
of the given graph and choose a root for the tree. - Determine, for each edge uv that is not part of the tree, the distance between the root and the lowest common ancestorLowest common ancestorThe lowest common ancestor is a concept in graph theory and computer science. Let T be a rooted tree with n nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants .The LCA of v and w in T is the shared ancestor of v...
of u and v. - For each edge uv that is part of the tree, find the corresponding "master edge", a non-tree edge wx such that the cycle formed by adding wx to the tree passes through uv and such that, among such edges, w and x have a lowest common ancestor that is as close to the root as possible (with ties broken by edge identifiers).
- Form an ear for each non-tree edge, consisting of it and the tree edges for which it is the master, and order the ears by their master edges' distance from the root (with the same tie-breaking rule).
These algorithms may be used as subroutines for other problems including testing connectivity, recognizing series-parallel graphs, and constructing st-numberings of graphs (an important subroutine in planarity testing
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
).