In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits

Series and parallel circuits

Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel and occur very frequently. Components connected in series are connected along a single path, so the same current flows through all of the...

.

Definition and terminology

In this context, the term graph means multigraph

Multigraph

In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....

.

There are several ways to define series-parallel graphs. The following definition basically follows the one used in .

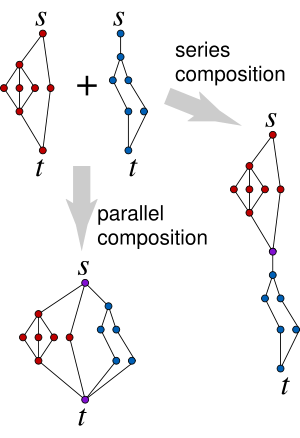
A two-terminal graph (TTG) is a graph with two distinguished vertices, s and t called source and sink, respectively.

The parallel composition Pc = Pc(X,Y) of two TTGs X and Y is a TTG created from the disjoint union of graphs X and Y by merging the sources of X and Y to create the source of Pc and merging the sinks of X and Y to create the sink of Pc.

The series composition Sc = Sc(X,Y) of two TTGs X and Y is a TTG created from the disjoint union of graphs X and Y by merging the sink of X with the source of Y. The source of X becomes the source of Sc and the sink of Y becomes the sink of Sc.

A two-terminal series-parallel graph (TTSPG) is a graph that may be constructed by a sequence of series and parallel compositions starting from a set of copies of a single-edge graph K

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

₂ with assigned terminals.

Definition 1. Finally, a graph is called series-parallel (sp-graph), if it is a TTSPG when some two of its vertices are regarded as source and sink.

In a similar way one may define series-parallel digraphs, constructed from copies of single-arc graphs, with arcs directed from the source to the sink.

Alternative definition

The following definition specifies the same class of graphs.

Definition 2. A graph is an sp-graph, if it may be turned into K

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

₂ by a sequence of the following operations:

• Replacement of a pair of parallel edges with a single edge that connects their common endpoints
• Replacement of a pair of edges incident to a vertex of degree 2 other than s or t with a single edge.

Properties

Every series-parallel graph has treewidth at most 2 and branchwidth at most 2. Indeed, a graph has treewidth at most 2 if and only if it has branchwidth at most 2, if and only if every biconnected component

Biconnected component

In graph theory, a biconnected component is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points...

 is a series-parallel graph. The maximal

Maximal element

In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...

 series-parallel graphs, graphs to which no additional edges can be added without destroying their series-parallel structure, are exactly the 2-trees

K-tree

In graph theory, a k-tree is a chordal graph all of whose maximal cliques are the same size k + 1 and all of whose minimal clique separators are also all the same size k....

. Graphs of treewidth at most 2 have an explicit forbidden minor characterization, implying that a graph is series-parallel if and only if its biconnected components

Biconnected graph

In the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...

 are linked in a path and it excludes the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

 K₄ as a minor.

Series parallel graphs may also be characterized by their ear decomposition

Ear decomposition

In graph theory, an ear of an undirected graph G is a path P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree two in P...

s.

Research involving series-parallel graphs

SPGs may be recognized in linear time and their series-parallel decomposition may be constructed in linear time as well.

Besides being a model of certain types of electric networks, these graphs are of interest in computational complexity theory

Computational complexity theory

Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...

, because a number of standard graph problems are solvable in linear time on SPGs, including finding of the maximum matching, maximum independent set, minimum dominating set and Hamiltonian completion

Hamiltonian completion

The Hamiltonian completion problem is to find the minimal number of edges to add to a graph to make it Hamiltonian.The problem is clearly NP-hard in general case...

. Some of these problems are NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

 for general graphs. The solution capitalizes on the fact that if the answers for one of these problems are known for two SP-graphs, then one can quickly find the answer for their series and parallel compositions.

The series-parallel networks problem

Series-parallel networks problem

In combinatorial mathematics, the series-parallel networks problem asks for the number of series-parallel networks that can be formed using a given number of edges...

 refers to a graph enumeration

Graph enumeration

In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...

 problem which asks for the number of series-parallel graphs that can be formed using a given number of edges.

Generalization

The generalized series-parallel graphs (GSP-graphs) are an extension of the SPGs with the same algorithmic efficiency for the mentioned problems. The class of GSP-graphs include the classes of SP-graphs and outerplanar graph

Outerplanar graph

In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...

s.

GSP graphs may be specified by the Definition 2 augmented with the third operation of deletion of a dangling vertex (vertex of degree 1). Alternatively, Definition 1 may be augmented with the following operation.

• The source merge S = M(X,Y) of two TTGs X and Y is a TTG created from the disjoint union of graphs X and Y by merging the source of X with the source of Y. The source and sink of X become the source and sink of P respectively.

An SPQR tree is a tree structure that can be defined for an arbitrary 2-vertex-connected graph. It has S nodes that are analogous to the series composition operations in series-parallel graphs, P nodes that are analogous to the parallel composition operations in series-parallel graphs, and R nodes that do not correspond to series-parallel composition operations. A 2-connected graph is series-parallel if and only if there are no R nodes in its SPQR tree.