Element (category theory)
Encyclopedia
In category theory
, the concept of an element, or a point, generalizes the more usual set theoretic
concept of an element of a set to an object of any category
. This idea often allows to restate definitions or properties of morphisms (such as monomorphism
or product
) which are given by a universal property
in more familiar terms by stating their relation to elements. Some very general theorems, such as Yoneda's lemma and the Mitchell embedding theorem, are of great utility in this way, by allowing one to work in a context where these translations are valid. This approach to category theory, in particular the use of the Yoneda lemma in this way, may be due to Grothendieck, and is often called the method of the functor of points.
and A, T are two objects of C. A T-valued point of A is simply an arrow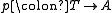
. The set of all T-valued points of A varies functorially with T, giving rise to the "functor of points" of A; according to the Yoneda lemma
, this completely determines A as an object of C.
if
Suppose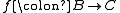
and 
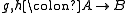in C. Then g and h are A-valued points of B, and therefore monomorphism is equivalent to the more familiar statement
Some care is necessary. f is an epimorphism
if the dual
condition holds:
In set theory, the term "epimorphism" is synonymous with "surjection", i.e.
This is clearly not the translation of the first statement into the language of points, and in fact these statements are not equivalent in general. However, in some contexts, such as abelian categories, "monomorphism" and "epimorphism" are backed by sufficiently strong conditions that in fact they do allow such a reinterpretation on points.
Similarly, categorical constructions such as the product
have pointed analogues. Recall that if A, B are two objects of C, their product A×B is an object such that
In this definition, f and g are T-valued points of A and B, respectively, while h is a T-valued point of A×B. An alternative definition of the product is therefore:
This is the more familiar definition of the product of two sets.
, Grothendieck introduced the notion of a scheme
in order to unify the subject with arithmetic geometry, which dealt with the same idea of studying solutions to polynomial equations (i.e. algebraic varieties
) but where the solutions are not complex number
s but rational number
s, integer
s, or even elements of some finite field
. A scheme is then just that: a scheme for collecting together all the manifestations of a variety defined by the same equations but with solutions taken in different number sets. One scheme gives a complex variety, whose points are its
-valued points, as well as the set of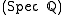 
-valued points (rational solutions to the equations), and even 
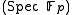-valued points (solutions modulo
p).
One feature of the language of points is evident from this example: it is, in general, not enough to consider just points with values in a single object. For example, the equation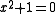
(which defines a scheme) has no real solutions, but it has complex solutions, namely 
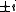. It also has one solution modulo 2 and two modulo 5, 13, 29, etc. (all primes which are 1 modulo 4). Just taking the real solutions would give no information whatsoever.
s of {1}).
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the concept of an element, or a point, generalizes the more usual set theoretic
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
concept of an element of a set to an object of any category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. This idea often allows to restate definitions or properties of morphisms (such as monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
or product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
) which are given by a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in more familiar terms by stating their relation to elements. Some very general theorems, such as Yoneda's lemma and the Mitchell embedding theorem, are of great utility in this way, by allowing one to work in a context where these translations are valid. This approach to category theory, in particular the use of the Yoneda lemma in this way, may be due to Grothendieck, and is often called the method of the functor of points.
Definition
Suppose C is any categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and A, T are two objects of C. A T-valued point of A is simply an arrow
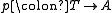. The set of all T-valued points of A varies functorially with T, giving rise to the "functor of points" of A; according to the Yoneda lemmaYoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
, this completely determines A as an object of C.
Properties of morphisms
Many properties of morphisms can be restated in terms of points. For example, a map f is said to be a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
if
- For any appropriate maps g, h such that
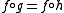, then 
.
Suppose
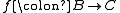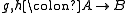and in C. Then g and h are A-valued points of B, and therefore monomorphism is equivalent to the more familiar statement
- f is a monomorphism if it is an injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
on points of B.
Some care is necessary. f is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
if the dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
condition holds:
- For any appropriate maps g, h such that
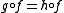, then 
.
In set theory, the term "epimorphism" is synonymous with "surjection", i.e.
- Every point of C is the image, under f, of some point of B.
This is clearly not the translation of the first statement into the language of points, and in fact these statements are not equivalent in general. However, in some contexts, such as abelian categories, "monomorphism" and "epimorphism" are backed by sufficiently strong conditions that in fact they do allow such a reinterpretation on points.
Similarly, categorical constructions such as the product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
have pointed analogues. Recall that if A, B are two objects of C, their product A×B is an object such that
- There exist maps
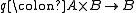, and for any T and maps 
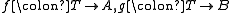, there exists a unique map 
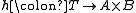such that 
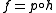and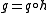 
.
In this definition, f and g are T-valued points of A and B, respectively, while h is a T-valued point of A×B. An alternative definition of the product is therefore:
- A×B is an object of C, together with projection maps
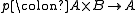and 
, such that p and q furnish a bijection between points of A×B and pairs of points of A and B.
This is the more familiar definition of the product of two sets.
Geometric origin
The terminology is geometric in origin; in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Grothendieck introduced the notion of a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
in order to unify the subject with arithmetic geometry, which dealt with the same idea of studying solutions to polynomial equations (i.e. algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
) but where the solutions are not complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s but rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, or even elements of some finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. A scheme is then just that: a scheme for collecting together all the manifestations of a variety defined by the same equations but with solutions taken in different number sets. One scheme gives a complex variety, whose points are its
-valued points, as well as the set of 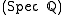-valued points (rational solutions to the equations), and even 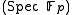-valued points (solutions moduloModulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
p).
One feature of the language of points is evident from this example: it is, in general, not enough to consider just points with values in a single object. For example, the equation
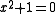(which defines a scheme) has no real solutions, but it has complex solutions, namely 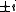. It also has one solution modulo 2 and two modulo 5, 13, 29, etc. (all primes which are 1 modulo 4). Just taking the real solutions would give no information whatsoever.Relation with set theory
The situation is analogous to the case where C is the category, Sets, of sets of actual elements. In this case, we have the "one-pointed" set {1}, and the elements of any set S are the same as the {1}-valued points of S. In addition, though, there are the {1,2}-valued points, which are pairs of elements of S, or elements of S×S. In the context of sets, these higher points are extraneous: S is determined completely by its {1}-points. However, as shown above, this is special (in this case, it is because all sets are iterated coproductCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s of {1}).