Epicycloid
Encyclopedia
In geometry
, an epicycloid is a plane curve
produced by tracing the path of a chosen point of a circle
— called an epicycle
— which rolls without slipping around a fixed circle. It is a particular kind of roulette
.
If the smaller circle has radius r, and the larger circle has radius R = kr, then the
parametric equations for the curve can be given by either:
or:
If k is an integer, then the curve is closed, and has k cusp
s (i.e., sharp corners, where the curve is not
differentiable).
If k is a rational number
, say k=p/q expressed in simplest terms, then the curve has p cusps.
If k is an irrational number
, then the curve never closes, and forms a dense subset
of the space between the larger circle and a circle of radius R + 2r.
The epicycloid is a special kind of epitrochoid
.
An epicycle with one cusp is a cardioid
.
An epicycloid and its evolute
are similar
.http://mathworld.wolfram.com/EpicycloidEvolute.html
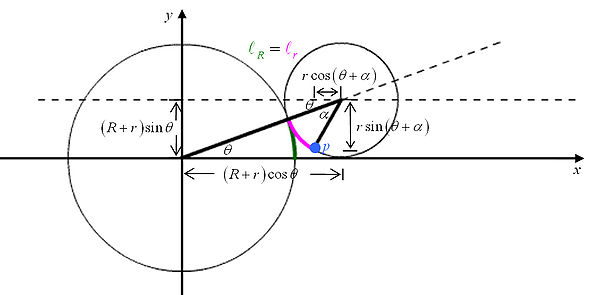We assume that the position of 
is what we want to solve, 
is the radian from the tangential point to the moving point 
, and 
is the radian from the starting point to the tangential point.
Since there is no sliding between the two cycles, then we have that
By the definition of radian (which is the rate arc over radius), then we have that
From the two condition, we get the identity
By calculating, we get the relation between
and 
, which is
From the figure, we see the position of the point
clearly.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an epicycloid is a plane curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
produced by tracing the path of a chosen point of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
— called an epicycle
Deferent and epicycle
In the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
— which rolls without slipping around a fixed circle. It is a particular kind of roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
.
If the smaller circle has radius r, and the larger circle has radius R = kr, then the
parametric equations for the curve can be given by either:
or:
If k is an integer, then the curve is closed, and has k cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
s (i.e., sharp corners, where the curve is not
differentiable).
If k is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, say k=p/q expressed in simplest terms, then the curve has p cusps.
If k is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, then the curve never closes, and forms a dense subset
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of the space between the larger circle and a circle of radius R + 2r.
The epicycloid is a special kind of epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
.
An epicycle with one cusp is a cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
.
An epicycloid and its evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.http://mathworld.wolfram.com/EpicycloidEvolute.html
Proof
is what we want to solve, is the radian from the tangential point to the moving point , and is the radian from the starting point to the tangential point.Since there is no sliding between the two cycles, then we have that
By the definition of radian (which is the rate arc over radius), then we have that
From the two condition, we get the identity
By calculating, we get the relation between
and , which isFrom the figure, we see the position of the point
clearly.See also
- Special cases: CardioidCardioidA cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
, NephroidNephroidThe nephroid is a plane curve whose name means kidney-shaped Although the term nephroid was used to describe other curves, it was applied to the curve in this article by Proctor in 1878. This and the information below may be verified in Lockwood, pp... - CycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
- HypocycloidHypocycloidIn geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
- EpitrochoidEpitrochoidAn epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
- HypotrochoidHypotrochoidA hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
- SpirographSpirographSpirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...
- Deferent and epicycleDeferent and epicycleIn the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
- Epicyclic gearingEpicyclic gearingEpicyclic gearing or planetary gearing is a gear system consisting of one or more outer gears, or planet gears, revolving about a central, or sun gear. Typically, the planet gears are mounted on a movable arm or carrier which itself may rotate relative to the sun gear...
External links
- Epicycloid, MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- "Epicycloid" by Michael Ford, The Wolfram Demonstrations Project, 2007