
Nephroid
Encyclopedia
The nephroid is a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
whose name means kidney-shaped (compare nephrology
Nephrology
Nephrology is a branch of internal medicine and pediatrics dealing with the study of the function and diseases of the kidney.-Scope of the specialty:...
.) Although the term nephroid was used to describe other curves, it was applied to the curve in this article by Proctor in 1878. This and the information below may be verified in Lockwood, pp. 62-71 (see References).
Parametric equations
Parametric equations for the nephroid shown above, with cusps on the x-axis, are given by
When the cusps lie on the y-axis, parametric equations are given by

Cartesian equation
A Cartesian equation for the nephroid is
Properties
Note: All properties refer to the nephroid as parameterized by the first pair of equations above.The arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
and area of the nephroid are, respectively,

The radius of curvature
Radius of curvature (mathematics)
In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
is given by

...a caustic of a circle
A nephroid may be viewed as a causticCaustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
of a circle for parallel rays. In other words, if a circle reflected parallel rays of light, the reflected rays would envelope a nephroid. Two such reflected rays are shown in blue.
This reflective property explains why a bright light produces a nephroid-shaped reflection at the bottom of a coffee mug.
Note: In the figure, the parallel rays intersect the circle at points spaced 4 degrees apart around its circumference.
...an envelope of circles
A nephroid may be created as an envelopeEnvelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of circles. Begin with a base circle (blue), then select a point on this circle (red dot). With this point as center, draw a circle (red) tangent to the y-axis. When several such circles are drawn, the image of a nephroid is produced.
Note: In the figure, there are 36 circles whose centers are spaced 10 degrees apart on the base circle.
...an envelope of lines
A nephroid may be created as an envelopeEnvelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of lines. Begin with a circle of radius a. For various values of t, join the points which are t degrees and 3t degrees around this circle. In other words, join the points
 and
and  These lines envelop a nephroid.
These lines envelop a nephroid.Note: In the figure, there are 90 lines corresponding to the parameter t taking on values which are multiples of 4.
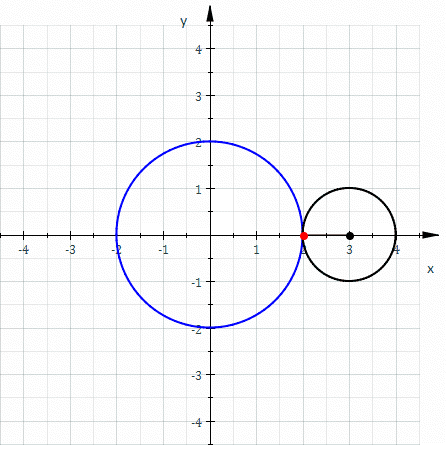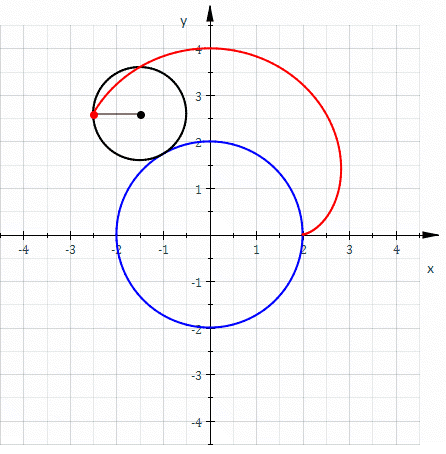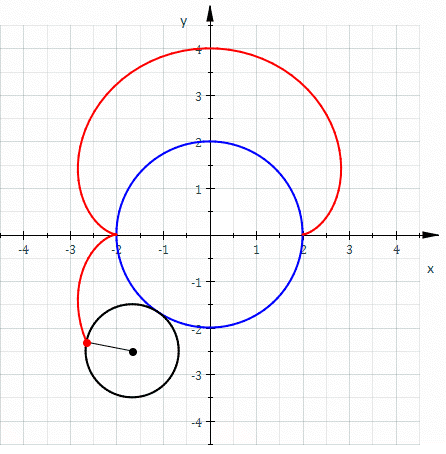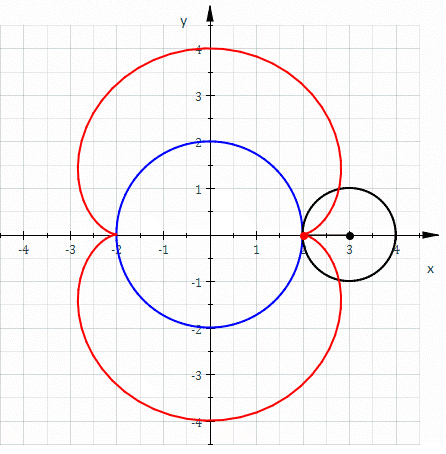
...an epicycloid of two cusps

Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
of two cusps. In the figure at the top of the article, the small black circle of radius a is externally tangent to the larger blue circle of radius 2a. As the smaller circle rolls around the larger circle without slipping, the red point traces out a nephroid.
This figure shows the nephroid as an epicycloid
Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
in another way. The large black circle of radius 3a is internally tangent to the smaller blue circle of radius 2a. As the larger circle rolls around the smaller circle without slipping, the red point traces out a nephroid.
The evolute...
The evoluteEvolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of the nephroid is another nephroid half as large and rotated 90 degrees. The original nephroid is visible as an envelope of its osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
s (gray). Two osculating circles are shown (blue). The centers of these circles are seen to lie on the evolute (smaller nephroid, red).
Note: In the figure, there are 60 circles corresponding to the parameter t taking on values which are multiples of 6.
The involute...
Because the evolute of the nephroid is another nephroid, so the involuteInvolute
In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
of the nephroid is also another nephroid. The original nephroid (envelope of gray circles) in the previous image is the involute of the smaller red nephroid.
The inverse...
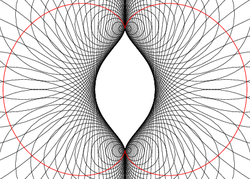
Inverting about a circle of radius a, a Cartesian equation for the inverse is


