Hypocycloid
Encyclopedia
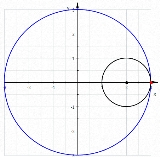
In geometry
, a hypocycloid is a special plane curve
generated by the trace of a fixed point on a small circle
that rolls within a larger circle. It is comparable to the cycloid
but instead of the circle rolling along a line, it rolls within a circle.
parametric equations for the curve can be given by either:

or:

If k is an integer, then the curve is closed, and has k cusps
(i.e., sharp corners, where the curve is not
differentiable). Specially for k=2 the curve is a straight line and the circles are called Cardano circles. Girolamo Cardano was the first to describe these hypocycloids, which had applications in the technology of high-speed printing press
.
If k is a rational number
, say k = p/q expressed in simplest terms, then the curve has p cusps.
If k is an irrational number
, then the curve never closes, and fills the space between the larger circle and a circle of radius R − 2r.
Each hypocycloid (for any value of r) is a brachistochrone for the gravitational potential inside a homogeneous sphere of radius R.
, which are a particular kind of roulette.
A hypocycloid with three cusps is known as a deltoid
.
A hypocycloid curve with four cusps is known as an astroid.
of a hypocycloid is an enlarged version of the hypocycloid itself, while
the involute
of a hypocycloid is a reduced copy of itself. http://mathworld.wolfram.com/HypocycloidEvolute.html
The pedal
of a hypocycloid with pole at the center of the hypocycloid is a rose curve.
The isoptic
of a hypocycloid is a hypocycloid.
toy. Specifically, the Spirograph can draw hypotrochoid
s and epitrochoid
s.
The Pittsburgh Steelers
' logo, which is based on the Steelmark
, includes three astroids (hypocycloids of four cusp
s). In his weekly NFL.com column Tuesday Morning Quarterback, Gregg Easterbrook
, often refers to the Steelers as the Hypocycloids.
The flag of Portland, Oregon
features an astroid, a hypocycloid of four cusps.
The 2007 redesign of The Price is Right
s set features astroids on the three main doors and the turntable area. http://www.tvsquad.com/2007/08/21/a-glimpse-at-drew-careys-price-is-right/
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hypocycloid is a special plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
generated by the trace of a fixed point on a small circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
that rolls within a larger circle. It is comparable to the cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
but instead of the circle rolling along a line, it rolls within a circle.
Properties
If the smaller circle has radius r, and the larger circle has radius R = kr, then theparametric equations for the curve can be given by either:


or:


If k is an integer, then the curve is closed, and has k cusps
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
(i.e., sharp corners, where the curve is not
differentiable). Specially for k=2 the curve is a straight line and the circles are called Cardano circles. Girolamo Cardano was the first to describe these hypocycloids, which had applications in the technology of high-speed printing press
Printing press
A printing press is a device for applying pressure to an inked surface resting upon a print medium , thereby transferring the ink...
.
If k is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, say k = p/q expressed in simplest terms, then the curve has p cusps.
If k is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, then the curve never closes, and fills the space between the larger circle and a circle of radius R − 2r.
Each hypocycloid (for any value of r) is a brachistochrone for the gravitational potential inside a homogeneous sphere of radius R.
Examples
The hypocycloid is a special kind of hypotrochoidHypotrochoid
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
, which are a particular kind of roulette.
A hypocycloid with three cusps is known as a deltoid
Deltoid curve
In geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
.
A hypocycloid curve with four cusps is known as an astroid.
Derived curves
The evoluteEvolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of a hypocycloid is an enlarged version of the hypocycloid itself, while
the involute
Involute
In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
of a hypocycloid is a reduced copy of itself. http://mathworld.wolfram.com/HypocycloidEvolute.html
The pedal
Pedal curve
In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....
of a hypocycloid with pole at the center of the hypocycloid is a rose curve.
The isoptic
Isoptic
In the geometry of curves, an isoptic is the set of points for which two tangents of a given curve meet at a given angle. The orthoptic is the isoptic whose given angle is a right angle....
of a hypocycloid is a hypocycloid.
Hypocycloids in popular culture
Curves similar to hypocyloids can be drawn with the SpirographSpirograph
Spirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...
toy. Specifically, the Spirograph can draw hypotrochoid
Hypotrochoid
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
s and epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
s.
The Pittsburgh Steelers
Pittsburgh Steelers
The Pittsburgh Steelers are a professional football team based in Pittsburgh, Pennsylvania. The team currently belongs to the North Division of the American Football Conference in the National Football League . Founded in , the Steelers are the oldest franchise in the AFC...
' logo, which is based on the Steelmark
Steelmark
The Steelmark is a logo representing steel and the steel industry owned by the American Iron and Steel Institute, and used by it to promote the product and its manufacturers....
, includes three astroids (hypocycloids of four cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
s). In his weekly NFL.com column Tuesday Morning Quarterback, Gregg Easterbrook
Gregg Easterbrook
Gregg Edmund Easterbrook is an American writer, lecturer, and a senior editor of The New Republic. His articles have appeared in Slate, The Atlantic Monthly, The New York Times, The Washington Post, The Los Angeles Times, Reuters, Wired, and Beliefnet. In addition, he was a fellow at the...
, often refers to the Steelers as the Hypocycloids.
The flag of Portland, Oregon
Flag of Portland, Oregon
The city flag of Portland, Oregon, consists of a green field on which is placed a white four-pointed directional star from which radiate blue stripes, each bordered by L-shaped yellow elements. Narrow white fimbriations separate the blue and yellow elements from each other and from the green...
features an astroid, a hypocycloid of four cusps.
The 2007 redesign of The Price is Right
The Price Is Right
The Price Is Right is a television game show franchise originally produced by Mark Goodson and Bill Todman, and created by Bob Stewart, and is currently produced and owned by FremantleMedia. The franchise centers on television game shows, but also includes merchandise such as video games, printed...
s set features astroids on the three main doors and the turntable area. http://www.tvsquad.com/2007/08/21/a-glimpse-at-drew-careys-price-is-right/
See also
- Special cases: Astroid, DeltoidDeltoid curveIn geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
- CycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
- EpicycloidEpicycloidIn geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
- HypotrochoidHypotrochoidA hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
- EpitrochoidEpitrochoidAn epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
- SpirographSpirographSpirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced...

