Fork-join queue
Encyclopedia
In queueing theory
, a discipline within the mathematical theory of probability
, a fork-join queue is a queue where incoming jobs are split on arrival for service by numerous servers and joined before departure. The model is often used for parallel computations or systems where products need to be obtained simultaneously from different suppliers (in a warehouse or manufacturing setting). The key quantity of interest in this model is usually the time taken to service a complete job. The model has been described as a "key model for the performance analysis of parallel
and distributed systems
." Few analytical results exist for fork-join queues, but various approximations are known.
The situation where jobs arrive according to a Poisson process
and service times are exponentially distributed is sometimes referred to as a Flatto–Hahn–Wright model or FHW model.
For the fork-join queue to be stable the input rate must be strictly less than sum of the service rates at the service nodes.
systems, parallel computations and for modelling order fulfilment in warehouses.
or a general distribution.
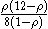
where
In the situation where nodes are M/M/1 queues and N > 2, Varki's modification of mean value analysis
can also be used to give an approximate value for the average response time.
For general service times (where each node is an M/G/1 queue
) Baccelli and Makowski give bounds for the average response time and higher moments
of this quantity both in the transient and steady state situations. Kemper and Mandjes show that for some parameters these bounds are not tight and show demonstrate an approximation technique.
techniques. Pinotsi and Zazanis show that a product form solution
exists when arrivals are deterministic as the queue lengths are then independent D/M/1 queues.
are considered by Li and Zhao.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a discipline within the mathematical theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a fork-join queue is a queue where incoming jobs are split on arrival for service by numerous servers and joined before departure. The model is often used for parallel computations or systems where products need to be obtained simultaneously from different suppliers (in a warehouse or manufacturing setting). The key quantity of interest in this model is usually the time taken to service a complete job. The model has been described as a "key model for the performance analysis of parallel
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
and distributed systems
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
." Few analytical results exist for fork-join queues, but various approximations are known.
The situation where jobs arrive according to a Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
and service times are exponentially distributed is sometimes referred to as a Flatto–Hahn–Wright model or FHW model.
Definition
On arrival at the fork point, a job is split into N sub-jobs which are served by each of the N servers. After service, sub-job wait until all other sub-jobs have also been processed. The sub-jobs are then rejoined and leave the system.For the fork-join queue to be stable the input rate must be strictly less than sum of the service rates at the service nodes.
Applications
Fork-join queues have been used to model zoned RAIDRAID
RAID is a storage technology that combines multiple disk drive components into a logical unit...
systems, parallel computations and for modelling order fulfilment in warehouses.
Response time
The response time (or sojourn time) is the total amount of time a job spends in the system.Distribution
Ko and Serfozo give an approximation for the response time distribution when service times are exponentially distributed and jobs arrive either according to a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
or a general distribution.
Average response time
An exact formula for the average response time is only known in the case of two servers (N=2) with exponentially distributed service times (where each server is an M/M/1 queue). In this situation, the response time (total time a job spends in the system) is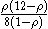where
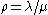is the utilizationUtilizationUtilization is a statistical concept as well as a primary business measure for the rental industry.-Queueing theory:In queueing theory, utilization is the proportion of the system's resources which is used by the traffic which arrives at it. It should be strictly less than one for the system to...
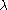is the arrival rate of jobs to the system
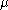is the total service rate across all the nodes.
In the situation where nodes are M/M/1 queues and N > 2, Varki's modification of mean value analysis
Mean value analysis
In queueing theory, a specialty within the mathematical theory of probability, mean value analysis is a technique for computing expected queue lengths in equilibrium for a closed separable system of queues...
can also be used to give an approximate value for the average response time.
For general service times (where each node is an M/G/1 queue
M/G/1 queue
In queueing theory, a discipline within the mathematical theory of probability, a M/G/1 queue represents the queue length in a system having a single server, where arrivals are detemined by a Poisson process and job service times can have an arbitrary distribution...
) Baccelli and Makowski give bounds for the average response time and higher moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of this quantity both in the transient and steady state situations. Kemper and Mandjes show that for some parameters these bounds are not tight and show demonstrate an approximation technique.
Stationary distribution
In general the stationary distribution of the number of jobs at each queue is intractable. Flatto considered the case of two servers (N=2) and derived the stationary distribution for the number of jobs at each queue via uniformizationUniformization (probability theory)
In probability theory, uniformization method, is a method to transient solutions of continuous-time Markov chains. The word uniformization in its narrower sense involves the transformation of a continuous time Markov chain to an analgous discrete time Markov chain....
techniques. Pinotsi and Zazanis show that a product form solution
Product form solution
In probability theory, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components...
exists when arrivals are deterministic as the queue lengths are then independent D/M/1 queues.
Join queue distribution
Once jobs are served, the parts are reassembled at the join queue. Nelson and Tantawi published the distribution of the join queue length in the situation where all servers have the same service rate. Heterogeneous service rates and distribution asymptotic analysisAsymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
are considered by Li and Zhao.