Formula for primes
Encyclopedia
In number theory
, a formula for primes is a formula generating the prime number
s, exactly and without exception. No such formula which is easily computable is presently known. A number of constraints are known: what such a "formula" can and cannot be.
polynomial
function P(n) with integer coefficients exists that evaluates to a prime number
for all integers n. The proof is: Suppose such a polynomial existed. Then P(1) would evaluate to a prime p, so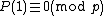
. But for any k, 
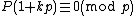also, so 
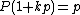(as it is prime and divisible by p), but the only way 
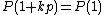for all k is if the polynomial function is constant.
The same reasoning shows an even stronger result: no non-constant polynomial function P(n) exists that evaluates to a prime number for almost all
integers n.
Euler
first noticed (in 1772) that the quadratic polynomial
is prime for all positive integers less than 41. The primes for n = 1, 2, 3... are 41, 43, 47, 53, 61, 71... The differences between the terms are 2, 4, 6, 8, 10... For n = 41, it produces a square number, 1681, which is equal to 41×41, the smallest composite number
for this formula. If 41 divides n it divides P(n) too. The phenomenon is related to the Ulam spiral
, which is also implicitly quadratic, and the class number;
this polynomial is related to the Heegner number
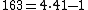, and there are analogous polynomials for 
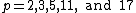, corresponding to other Heegner numbers.
It is known, based on Dirichlet's theorem on arithmetic progressions
, that linear polynomial functions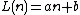
produce infinitely many primes as long as a and b are relatively prime (though no such function will assume prime values for all values of n). Moreover, the Green–Tao theorem says that for any k there exists a pair of a and b with the property that 
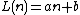is prime for any n from 0 to k − 1. However, the best known result of such type is for k = 26:
It is not even known whether there exists a univariate polynomial of degree at least 2 that assumes an infinite number of values that are prime; see Bunyakovsky conjecture
.
s in 26 variables can be used to obtain a Diophantine representation of the set of all primes. proved that a given number k + 2 is prime if and only if
the following system of 14 Diophantine equations has a solution in the natural number
s:
The 14 equations α0, …, α13 can be used to produce a prime-generating polynomial inequality in 26 variables:
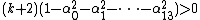
i.e.:
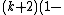
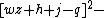
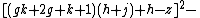
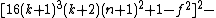
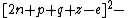
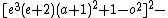
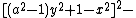
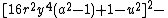
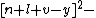
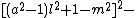
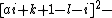
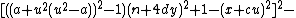
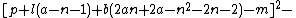
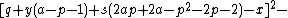
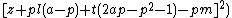
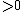
is a polynomial inequality in 26 variables, and the set of prime numbers is identical to the set of positive values taken on by this polynomial inequality as the variables a, b, …, z range over the nonnegative integers.
A general theorem of Matiyasevich
says that if a set is defined by a system of Diophantine equations, it can also be defined by a system of Diophantine equations in only 9 variables. Hence, there is a prime-generating polynomial as above with only 10 variables. However, its degree is large (in the order of 1045). On the other hand, there also exists such a set of equations of degree only 4, but in 58 variables.
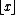(defined to be the largest integer less than or equal to the real number
x), one can construct several formulas that take only prime numbers as values for all positive integers n.
A such that
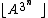
is a prime number for all positive integers n. If the Riemann hypothesis
is true, then the smallest such A has a value of around 1.3063... and is known as Mills' constant. This formula has no practical value, because very little is known about the constant (not even whether it is rational
), and there is no known way of calculating the constant without finding primes in the first place.
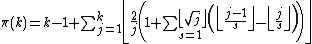
Note the following equalities:
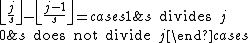
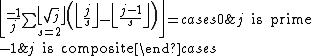
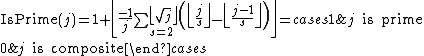
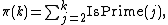
where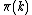
is the prime counting function
.
can be used as the basis for a prime number formula. In effect, a test for the primality of n is a computation of the function IsPrime(n), defined by: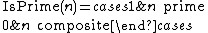
If the primality test is given by a condition on some formula involving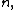
then that formula gives a formula for IsPrime(n). Using a product,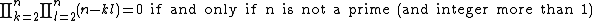
For a prime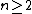
,the product above is not 0. So,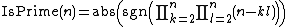
where n is more than 1. However, the product is very large or very small where n is a prime so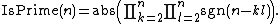
Moreover, we need not calculate product up to k=l=n.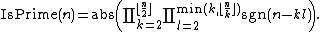
Wilson's theorem states that n is prime if and only if
it divides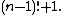
To express this by an explicit formula, two intermediate functions are introduced: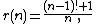
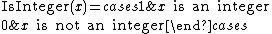
Then Wilson's theorem says that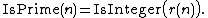
This can be further specified by an explicit formula for IsInteger(x). Some options are: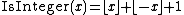
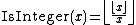
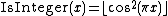: formula by C. P. Willans
Then, for example, taking the first option gives a formula for IsPrime(n) using Wilson's theorem: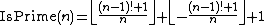
Not using the function IsInteger,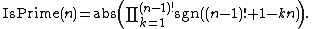
Once IsPrime(n) can be computed, the prime counting function
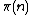can as well, since by definition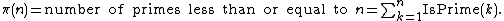
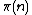can then compute a function testing whether a given integer n is the mth prime: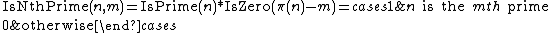
The function IsZero(x) can likewise be expressed by a formula: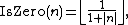
Finally, the IsNthPrime(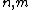
) function can be used to produce a formula for the nth prime: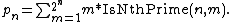
The upper bound 2n comes from Bertrand's postulate, which implies that there is a sequence of primes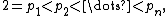
where 
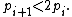Thus,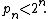 
Substituting the formulas above and applying Wilson's theorem gives a formula for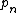
involving the arithmetic operations and the floor function. Other such formulas are: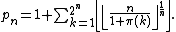
in which the following equality is important: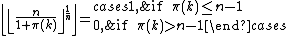
and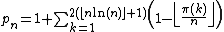
by Sebastián Martín-Ruiz and proved with Jonathan Sondow . A similar formula for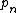
was given earlier by Stephen Regimbal .
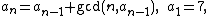
where gcd(x, y) denotes the greatest common divisor
of x and y. The sequence of differences an + 1 − an starts with 1, 1, 1, 5, 3, 1, 1, 1, 1, 11, 3, 1, 1 . proved that this sequence contains only ones and prime numbers.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a formula for primes is a formula generating the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, exactly and without exception. No such formula which is easily computable is presently known. A number of constraints are known: what such a "formula" can and cannot be.
Prime formulas and polynomial functions
It is known that no non-constantConstant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function P(n) with integer coefficients exists that evaluates to a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
for all integers n. The proof is: Suppose such a polynomial existed. Then P(1) would evaluate to a prime p, so
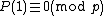. But for any k, 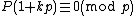also, so 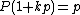(as it is prime and divisible by p), but the only way 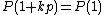for all k is if the polynomial function is constant.The same reasoning shows an even stronger result: no non-constant polynomial function P(n) exists that evaluates to a prime number for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
integers n.
Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
first noticed (in 1772) that the quadratic polynomial
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
- P(n) = n2 - n + 41
is prime for all positive integers less than 41. The primes for n = 1, 2, 3... are 41, 43, 47, 53, 61, 71... The differences between the terms are 2, 4, 6, 8, 10... For n = 41, it produces a square number, 1681, which is equal to 41×41, the smallest composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
for this formula. If 41 divides n it divides P(n) too. The phenomenon is related to the Ulam spiral
Ulam spiral
The Ulam spiral, or prime spiral is a simple method of visualizing the prime numbers that reveals the apparent tendency of certain quadratic polynomials to generate unusually large numbers of primes...
, which is also implicitly quadratic, and the class number;
this polynomial is related to the Heegner number
Heegner number
In number theory, a Heegner number is a square-free positive integer d such that the imaginary quadratic field Q has class number 1...
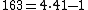, and there are analogous polynomials for 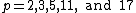, corresponding to other Heegner numbers.It is known, based on Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
, that linear polynomial functions
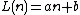produce infinitely many primes as long as a and b are relatively prime (though no such function will assume prime values for all values of n). Moreover, the Green–Tao theorem says that for any k there exists a pair of a and b with the property that 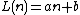is prime for any n from 0 to k − 1. However, the best known result of such type is for k = 26:
- 43142746595714191 + 5283234035979900n is prime for all n from 0 to 25 .
It is not even known whether there exists a univariate polynomial of degree at least 2 that assumes an infinite number of values that are prime; see Bunyakovsky conjecture
Bunyakovsky conjecture
The Bunyakovsky conjecture stated in 1857 by the Russian mathematician Viktor Bunyakovsky, claims that an irreducible polynomial of degree two or higher with integer coefficients generates for natural arguments either an infinite set of numbers with greatest common divisor exceeding unity, or...
.
Formula based on a system of Diophantine equations
A system of 14 Diophantine equationDiophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s in 26 variables can be used to obtain a Diophantine representation of the set of all primes. proved that a given number k + 2 is prime if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the following system of 14 Diophantine equations has a solution in the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s:
- α0 =
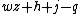= 0
- α1 =
= 0
- α2 =
= 0
- α3 =
= 0
- α4 =
= 0
- α5 =
= 0
- α6 =
= 0
- α7 =
= 0
- α8 =
= 0
- α9 =
= 0
- α10 =
= 0
- α11 =
= 0
- α12 =
= 0
- α13 =
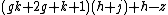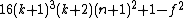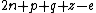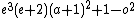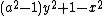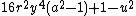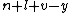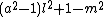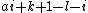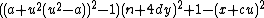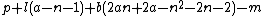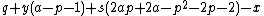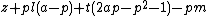= 0
The 14 equations α0, …, α13 can be used to produce a prime-generating polynomial inequality in 26 variables:
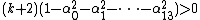
i.e.:
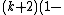
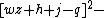
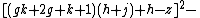
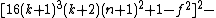
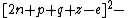
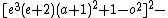
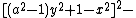
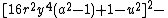
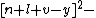
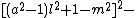
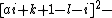
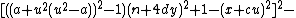
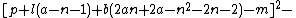
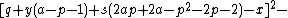
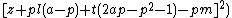
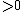
is a polynomial inequality in 26 variables, and the set of prime numbers is identical to the set of positive values taken on by this polynomial inequality as the variables a, b, …, z range over the nonnegative integers.
A general theorem of Matiyasevich
Yuri Matiyasevich
Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
says that if a set is defined by a system of Diophantine equations, it can also be defined by a system of Diophantine equations in only 9 variables. Hence, there is a prime-generating polynomial as above with only 10 variables. However, its degree is large (in the order of 1045). On the other hand, there also exists such a set of equations of degree only 4, but in 58 variables.
Formulas using the floor function
Using the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
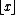(defined to be the largest integer less than or equal to the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x), one can construct several formulas that take only prime numbers as values for all positive integers n.
Mills's formula
The first such formula known was established in 1947 by W. H. Mills, who proved that there exists a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
A such that
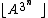
is a prime number for all positive integers n. If the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is true, then the smallest such A has a value of around 1.3063... and is known as Mills' constant. This formula has no practical value, because very little is known about the constant (not even whether it is rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
), and there is no known way of calculating the constant without finding primes in the first place.
Converting the sieve of Eratosthenes to prime number formulas
There is another, quite different formula discovered by Sebastián Martín-Ruiz and proved with Jonathan Sondow :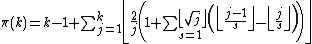Note the following equalities:
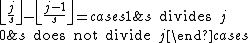
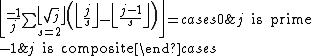
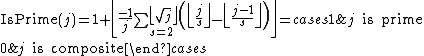
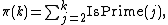
where
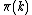is the prime counting functionPrime counting function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by \scriptstyle\pi .-History:...
.
Converting primality tests to prime number formulas
Any primality testPrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
can be used as the basis for a prime number formula. In effect, a test for the primality of n is a computation of the function IsPrime(n), defined by:
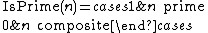
If the primality test is given by a condition on some formula involving
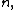then that formula gives a formula for IsPrime(n). Using a product,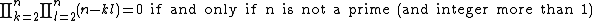For a prime
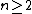,the product above is not 0. So,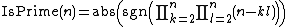where n is more than 1. However, the product is very large or very small where n is a prime so
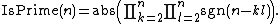
Moreover, we need not calculate product up to k=l=n.
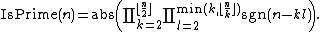
Wilson's theorem states that n is prime if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it divides
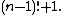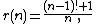
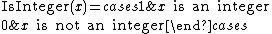
To express this by an explicit formula, two intermediate functions are introduced:Then Wilson's theorem says that
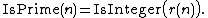
This can be further specified by an explicit formula for IsInteger(x). Some options are:
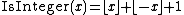
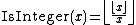
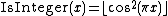: formula by C. P. Willans Then, for example, taking the first option gives a formula for IsPrime(n) using Wilson's theorem:
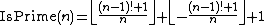
Not using the function IsInteger,
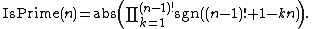
Once IsPrime(n) can be computed, the prime counting function
Prime counting function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by \scriptstyle\pi .-History:...
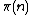can as well, since by definition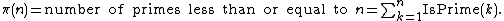 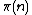can then compute a function testing whether a given integer n is the mth prime: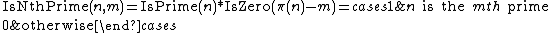The function IsZero(x) can likewise be expressed by a formula:
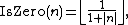
Finally, the IsNthPrime(
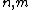) function can be used to produce a formula for the nth prime: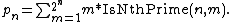The upper bound 2n comes from Bertrand's postulate, which implies that there is a sequence of primes
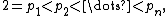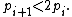where Thus, 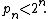Substituting the formulas above and applying Wilson's theorem gives a formula for
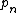involving the arithmetic operations and the floor function. Other such formulas are: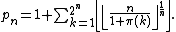in which the following equality is important:
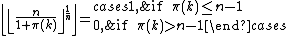
and
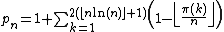
by Sebastián Martín-Ruiz and proved with Jonathan Sondow . A similar formula for
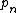was given earlier by Stephen Regimbal .Recurrence relation
Another prime generator is defined by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
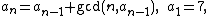
where gcd(x, y) denotes the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of x and y. The sequence of differences an + 1 − an starts with 1, 1, 1, 5, 3, 1, 1, 1, 1, 11, 3, 1, 1 . proved that this sequence contains only ones and prime numbers.