Fox n-coloring
Encyclopedia
In the mathematical
field of knot theory
, Fox n-coloring is a method of specifying a representation of a knot group
(or a link group
) onto the dihedral group of order n where n is an odd integer by coloring arcs in a link diagram (the representation itself is also often called a Fox n-coloring). Ralph Fox
discovered this method (and the special case of tricolorability
) "in an effort to make the subject accessible to everyone" when he was explaining knot theory to undergraduate students at Haverfold College in 1956. Fox n-coloring is an example of a conjugation quandle.
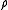of π onto 
the dihedral group of order 2n is called a Fox n-coloring (or simply an n-coloring) of L. A link L which admits such a representation is said to be n-colorable, and 
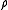is called an n-coloring of L. Such representations of link groups had been considered in the context of covering spaces since Reidemeister in 1929.
The link group is generated paths from a basepoint in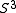
to the boundary of a tubular neighbourhood of the link, around a meridian of the tubular neighbourhood, and back to the basepoint. By surjectivity of the representation these generators must map to reflections of a regular n-gon. Such reflections correspond to elements 
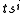of the dihedral group, where t is a reflection and s is a generating (
) rotation of the n-gon. The generators of the link group given above are in bijective correspondence with arcs of a link diagram, and if a generator maps to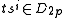 
we color the corresponding arc 
. This is called a Fox n-coloring of the link diagram, and it satisfies the following properties:
A n-colored link yields a 3-manifold
M by taking the (irregular) dihedral covering of the 3-sphere branched over L with monodromy
given by
. By a theorem of Montesinos and Hilden, and closed oriented 3-manifold may be obtained this way for some knot K any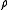 
some tricoloring
of K. This is no longer true when n is greater than three.
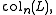
is an invariant of the link, which is easy to calculate by hand on any link diagram by coloring arcs according to the coloring rules. When counting colorings, by convention we also consider the case where all arcs are given the same color, and call such a coloring trivial.
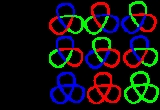
For example, the standard minimal crossing diagram of the Trefoil knot
has 9 distinct tricolorings as seen in the figure:
The set of Fox 'n'-colorings of a link forms an abelian group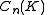
, where the sum of two n-colorings is the n-coloring obtained by strandwise addition. This group splits as a direct sum
,
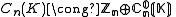where the first summand corresponds to the n trivial (constant) colors, and nonzero elements of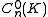
summand correspond to nontrivial n-colorings (modulo translations obtained by adding a constant to each strand).
If
is the connected sum
operator and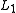
and 
are links, then
of π to G is called a G-coloring of L.
A G-coloring of a knot diagram is an induced assigning an element of G to the strands of L such that, at each crossing, if c is the element of G assigned to the overcrossing strand and if a and b are the elements of G assigned to the two undercrossing strands, then a = c-1 b c or b = c-1 a c, depending on the orientation of the overcrossing strand. If the group G is dihedral of order 2n, this diagrammatic represention of a G-coloring reduces to a Fox n-coloring. The torus knot
T(3,5) has only constant n-colorings, but for the group G equal to the alternating group A5, T(3,5) has non-constant G-colorings.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, Fox n-coloring is a method of specifying a representation of a knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
(or a link group
Link group
In knot theory, an area of mathematics, the link group of a link is an analog of the knot group of a knot. They were described by John Milnor in his Bachelor's thesis, .- Definition :...
) onto the dihedral group of order n where n is an odd integer by coloring arcs in a link diagram (the representation itself is also often called a Fox n-coloring). Ralph Fox
Ralph Fox
Ralph Hartzler Fox was an American mathematician. As a professor at Princeton University, he taught and advised many of the contributors to the Golden Age of differential topology, and he played an important role in the modernization and main-streaming of knot theory.Ralph Fox attended Swarthmore...
discovered this method (and the special case of tricolorability
Tricolorability
In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different knots...
) "in an effort to make the subject accessible to everyone" when he was explaining knot theory to undergraduate students at Haverfold College in 1956. Fox n-coloring is an example of a conjugation quandle.
Definition
Let L be a link, and let π be the fundamental group of its complement. A representation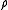 of π onto 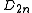the dihedral group of order 2n is called a Fox n-coloring (or simply an n-coloring) of L. A link L which admits such a representation is said to be n-colorable, and 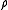is called an n-coloring of L. Such representations of link groups had been considered in the context of covering spaces since Reidemeister in 1929.The link group is generated paths from a basepoint in
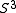to the boundary of a tubular neighbourhood of the link, around a meridian of the tubular neighbourhood, and back to the basepoint. By surjectivity of the representation these generators must map to reflections of a regular n-gon. Such reflections correspond to elements 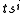of the dihedral group, where t is a reflection and s is a generating () rotation of the n-gon. 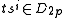The generators of the link group given above are in bijective correspondence with arcs of a link diagram, and if a generator maps to we color the corresponding arc . This is called a Fox n-coloring of the link diagram, and it satisfies the following properties:- At least two colors are used (by surjectivity of
). - Around a crossing, the average of the colors of the undercrossing arcs equals the color of the overcrossing arc (because
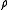is a representation of the link group).
A n-colored link yields a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
M by taking the (irregular) dihedral covering of the 3-sphere branched over L with monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
given by
. By a theorem of Montesinos and Hilden, and closed oriented 3-manifold may be obtained this way for some knot K any 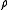some tricoloringTricolorability
In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different knots...
of K. This is no longer true when n is greater than three.
Number of colorings
The number of distinct Fox n-colorings of a link L, denoted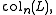is an invariant of the link, which is easy to calculate by hand on any link diagram by coloring arcs according to the coloring rules. When counting colorings, by convention we also consider the case where all arcs are given the same color, and call such a coloring trivial.
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
has 9 distinct tricolorings as seen in the figure:
- 3 "trivial" colorings (every arc blue, red, or green)
- 3 colorings with the ordering Blue→Green→Red
- 3 colorings with the ordering Blue→Red→Green
The set of Fox 'n'-colorings of a link forms an abelian group
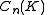, where the sum of two n-colorings is the n-coloring obtained by strandwise addition. This group splits as a direct sum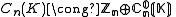,where the first summand corresponds to the n trivial (constant) colors, and nonzero elements of
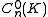summand correspond to nontrivial n-colorings (modulo translations obtained by adding a constant to each strand).If
is the connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
operator and
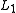and are links, then
Generalization to G-coloring
Let L be a link, and let π be the fundamental group of its complement, and let G be a group. A homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of π to G is called a G-coloring of L.A G-coloring of a knot diagram is an induced assigning an element of G to the strands of L such that, at each crossing, if c is the element of G assigned to the overcrossing strand and if a and b are the elements of G assigned to the two undercrossing strands, then a = c-1 b c or b = c-1 a c, depending on the orientation of the overcrossing strand. If the group G is dihedral of order 2n, this diagrammatic represention of a G-coloring reduces to a Fox n-coloring. The torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
T(3,5) has only constant n-colorings, but for the group G equal to the alternating group A5, T(3,5) has non-constant G-colorings.