
Goldner–Harary graph
Encyclopedia
In the mathematical
field of graph theory
, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary
, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph. The same graph had already been given as an example of a non-Hamiltonian simplicial polyhedron by Branko Grünbaum
in 1967.
: it can be drawn in the plane with none of its edges crossing. When drawn on a plane, all its faces are triangular, making it a maximal planar graph. As with every maximal planar graph, it is also 3-vertex-connected: the removal of any two of its vertices leaves a connected subgraph.
The Goldner–Harary graph is also non-hamiltonian. The smallest possible number of vertices for a non-hamiltonian polyhedral graph is 11. Therefore, the Goldner–Harary graph is a minimal example of graphs of this type. However, the Herschel graph
, another non-Hamiltonian polyhedron with 11 vertices, has fewer edges.
As a non-Hamiltonian maximal planar graph, the Goldner–Harary graph provides an example of a planar graph with book thickness
greater than two. Based on the existence of such examples, Bernhart and Kainen conjectured that the book thickness of planar graphs could be made arbitrarily large, but it was subsequently shown that all planar graphs have book thickness at most four.
It has book thickness 3, chromatic number 4, chromatic index 8, girth 3, radius 2, diameter 2 and is a 3-edge-connected graph
.
It is also a 3-tree
, and therefore it has treewidth 3. Like any k-tree, it is a chordal graph
. As a planar 3-tree, it forms an example of an Apollonian network
.
, the Goldner–Harary graph is a polyhedral graph
: it is planar and 3-connected, so there exists a convex polyhedron having the Goldner–Harary graph as its skeleton.
Geometrically, a polyhedron representing the Goldner–Harary graph may be formed by gluing a tetrahedron onto each face of a triangular dipyramid
, similarly to the way a triakis octahedron
is formed by gluing a tetrahedron onto each face of an octahedron
. That is, it is the Kleetope
of the triangular dipyramid. The dual graph
of the Goldner–Harary graph is represented geoemetrically by the truncation
of the triangular prism
.
of the Goldner–Harary graph is of order 12 and is isomorphic to the dihedral group
D6, the group of symmetries of a regular hexagon, including both rotations and reflections.
The characteristic polynomial
of the Goldner–Harary graph is :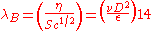 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary
Frank Harary
Frank Harary was a prolific American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory....
, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph. The same graph had already been given as an example of a non-Hamiltonian simplicial polyhedron by Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
in 1967.
Properties
The Goldner–Harary graph is a planar graphPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
: it can be drawn in the plane with none of its edges crossing. When drawn on a plane, all its faces are triangular, making it a maximal planar graph. As with every maximal planar graph, it is also 3-vertex-connected: the removal of any two of its vertices leaves a connected subgraph.
The Goldner–Harary graph is also non-hamiltonian. The smallest possible number of vertices for a non-hamiltonian polyhedral graph is 11. Therefore, the Goldner–Harary graph is a minimal example of graphs of this type. However, the Herschel graph
Herschel graph
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges, the smallest non-Hamiltonian polyhedral graph...
, another non-Hamiltonian polyhedron with 11 vertices, has fewer edges.
As a non-Hamiltonian maximal planar graph, the Goldner–Harary graph provides an example of a planar graph with book thickness
Book embedding
In graph theory, book embedding is a generalization of planar embedding to nonplanar surfaces in the form of a book, a collection of pages joined together at the spine of the book . The vertices of the graph are embedded on the spine, and each edge must lie in one of the pages...
greater than two. Based on the existence of such examples, Bernhart and Kainen conjectured that the book thickness of planar graphs could be made arbitrarily large, but it was subsequently shown that all planar graphs have book thickness at most four.
It has book thickness 3, chromatic number 4, chromatic index 8, girth 3, radius 2, diameter 2 and is a 3-edge-connected graph
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
.
It is also a 3-tree
K-tree
In graph theory, a k-tree is a chordal graph all of whose maximal cliques are the same size k + 1 and all of whose minimal clique separators are also all the same size k....
, and therefore it has treewidth 3. Like any k-tree, it is a chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
. As a planar 3-tree, it forms an example of an Apollonian network
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable...
.
Geometry
By Steinitz's theoremSteinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
, the Goldner–Harary graph is a polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
: it is planar and 3-connected, so there exists a convex polyhedron having the Goldner–Harary graph as its skeleton.
Geometrically, a polyhedron representing the Goldner–Harary graph may be formed by gluing a tetrahedron onto each face of a triangular dipyramid
Triangular dipyramid
In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces....
, similarly to the way a triakis octahedron
Triakis octahedron
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more...
is formed by gluing a tetrahedron onto each face of an octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. That is, it is the Kleetope
Kleetope
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid...
of the triangular dipyramid. The dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of the Goldner–Harary graph is represented geoemetrically by the truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
of the triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
.
Algebraic properties
The automorphism groupGraph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of the Goldner–Harary graph is of order 12 and is isomorphic to the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D6, the group of symmetries of a regular hexagon, including both rotations and reflections.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Goldner–Harary graph is :
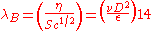 .
.

