
Goursat tetrahedron
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Goursat tetrahedron is a tetrahedral
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
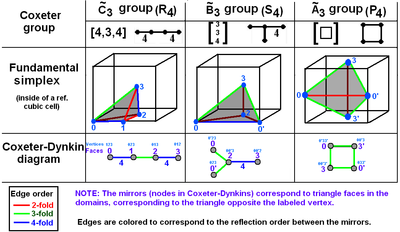
fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
of a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
. Each tetrahedral face represents a reflection hyperplane on 3-dimensional surfaces: the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, the Euclidean 3-space, and hyperbolic 3-space. Coxeter named after Edouard Goursat
Edouard Goursat
Édouard Jean-Baptiste Goursat was a French mathematician, now remembered principally as an expositor for his Cours d'analyse mathématique, which appeared in the first decade of the twentieth century. It set a standard for the high-level teaching of mathematical analysis, especially complex analysis...
who first looked into these domains. It is an extension of the theory of Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s for Wythoff constructions on the sphere.
Graphical representation
A Goursat tetrahedron can be represented graphically by a tetrahedral graph, which is in a dual configuration of the fundamental domain tetrahedron. In the graph, each node represents a face (mirror) of the Goursat tetrahedron. Each edge is labeled by a rational value corresponding to the reflection order, being π/dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
.
A 4-node Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
represents this tetrahedral graphs with order-2 edges hidden.
If some edges are order 2, the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
can be used for a simpler notation.
Existence requires each of the 3-node subgraphs of this graph, (p q r), (p u s), (q t u), and (r s t), must correspond to a Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
.
3-sphere (finite) solutions
The solutions for the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
with density 1 solutions are:
- DuoprismDuoprismIn geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s: [p]x[q], - Hyperprisms:
- [3,3]x[],
- [3,4]x[],
- [3,5]x[],
- Linear graphs: (Uniform polychoraUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
)- [3,3,3],
- [3,3,4],
- [3,4,3],
- [3,3,5],
- Tri-dental graphs:
- [31,1,1],
There are hundreds of rational solutions for the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, including these 6 linear graphs which generate the Schläfli-Hess polychora, and 11 nonlinear ones from Coxeter:
- Linear graphs
- Density 4: [3,5,5/2]
- Density 6: [5,5/2,5]
- Density 20: [5,3,5/2]
- Density 66: [5/2,5,5/2]
- Density 76: [5,5/2,3]
- Density 191: [3,3,5/2]
- Loop-n-tail graphs:
- Density 2:
- Density 3:
- Density 5:
- Density 8:
- Density 9:
- Density 14:
- Density 26:
- Density 30:
- Density 39:
- Density 46:
- Density 115:
Euclidean (affine) 3-space solutions
Density 1 solutions:- Convex uniform honeycombConvex uniform honeycombIn geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
:- Linear graph: [4,3,4],
- Tri-dental graph: [4,31,1],
- Loop graph: (3 3 3 3),
Hyperbolic 3-space solutions
Density 1 solutions:- Compact hyperbolic groups: (Convex uniform honeycombs in hyperbolic spaceConvex uniform honeycombs in hyperbolic spaceIn geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter–Dynkin...
)- Linear graphs:
- [3,5,3],
- [5,3,4],
- [5,3,5],
- Tri-dental graph:
- [5,31,1],
- Loop graphs:
- (4 3 3 3),
- (4 3 4 3),
- (5 3 3 3),
- (5 3 4 3),
- (5 3 5 3),
- Linear graphs:
- Noncompact hyperbolic groups (with affine subgraphs)
- Linear graphs: , , , , , ,
- Tri-dental graphs: , ,
- Loop graphs: , , , , , ,
- Loop-n-tail graphs: , , ,
- Two-loop graph:
- Simplex graph:

