
Gromov's systolic inequality for essential manifolds
Encyclopedia
In the mathematical
field of Riemannian geometry
, M. Gromov's systolic inequality bounds the length of the shortest non-contractible
loop on a Riemannian manifold
in terms of the volume of the manifold. Gromov's systolic inequality was proved in 1983; it can be viewed as a generalisation, albeit non-optimal, of Loewner's torus inequality
and Pu's inequality for the real projective plane.
Technically, let M be an essential
Riemannian manifold of dimension n; denote by sysπ1(M) the homotopy 1-systole of M, that is, the least length of a non-contractible loop on M. Then Gromov's inequality takes the form
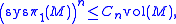
where Cn is a universal constant only depending on the dimension of M.
defines a nonzero element in the homology
of its fundamental group
, or more precisely in the homology of the corresponding Eilenberg–MacLane space. Here the fundamental class is taken in homology with integer coefficients if the manifold is orientable, and in coefficients modulo 2, otherwise.
Examples of essential manifolds include aspherical manifolds, real projective space
s, and lens space
s.
, the isoperimetric inequality
, the cone inequality, and the deformation theorem of Herbert Federer
.
and the filling volume of X. Namely, Gromov proved a sharp inequality relating the systole and the filling radius,
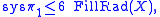
valid for all essential manifolds X; as well as an inequality
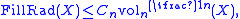
valid for all closed manifolds X.
It was shown by that the filling invariants, unlike the systolic invariants, are independent of the topology of the manifold in a suitable sense.
developed an alternative approach to the proof of Gromov's systolic inequality for essential manifolds.
. A uniform inequality for arbitrary 2-complexes with non-free fundamental groups is available, whose proof relies on the Grushko decomposition theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, M. Gromov's systolic inequality bounds the length of the shortest non-contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
loop on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in terms of the volume of the manifold. Gromov's systolic inequality was proved in 1983; it can be viewed as a generalisation, albeit non-optimal, of Loewner's torus inequality
Loewner's torus inequality
In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
and Pu's inequality for the real projective plane.
Technically, let M be an essential
Essential manifold
In mathematics, in algebraic topology and differential geometry, the notion of an essential manifold seems to have been first introduced explicitly in Mikhail Gromov's classic text in 1983 .-Definition:...
Riemannian manifold of dimension n; denote by sysπ1(M) the homotopy 1-systole of M, that is, the least length of a non-contractible loop on M. Then Gromov's inequality takes the form
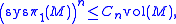
where Cn is a universal constant only depending on the dimension of M.
Essential manifolds
A closed manifold is called essential if its fundamental classFundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
defines a nonzero element in the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, or more precisely in the homology of the corresponding Eilenberg–MacLane space. Here the fundamental class is taken in homology with integer coefficients if the manifold is orientable, and in coefficients modulo 2, otherwise.
Examples of essential manifolds include aspherical manifolds, real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
s, and lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s.
Proofs of Gromov's inequality
Gromov's original 1983 proof is about 35 pages long. It relies on a number of techniques and inequalities of global Riemannian geometry. The starting point of the proof is the imbedding of X into the Banach space of Borel functions on X, equipped with the sup norm. The imbedding is defined by mapping a point p of X, to the real function on X given by the distance from the point p. The proof utilizes the coarea inequalityCoarea formula
In the mathematical field of geometric measure theory, the coarea formula expresses the integral of a function over an open set in Euclidean space in terms of the integral of the level sets of another function...
, the isoperimetric inequality
Isoperimetry
The isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter"...
, the cone inequality, and the deformation theorem of Herbert Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
.
Filling invariants and recent work
One of the key ideas of the proof is the introduction of filling invariants, namely the filling radiusFilling radius
In Riemannian geometry, the filling radius of a Riemannian manifold X is a metric invariant of X. It was originally introduced in 1983 by Mikhail Gromov, who used it to prove his systolic inequality for essential manifolds, vastly generalizing Loewner's torus inequality and Pu's inequality for the...
and the filling volume of X. Namely, Gromov proved a sharp inequality relating the systole and the filling radius,
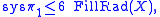
valid for all essential manifolds X; as well as an inequality
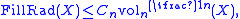
valid for all closed manifolds X.
It was shown by that the filling invariants, unlike the systolic invariants, are independent of the topology of the manifold in a suitable sense.
developed an alternative approach to the proof of Gromov's systolic inequality for essential manifolds.
Inequalities for surfaces and polyhedra
Stronger results are available for surfaces, where the asymptotics when the genus tends to infinity are by now well understood, see systoles of surfacesSystoles of surfaces
In mathematics, systolic inequalities for curves on surfaces were first studied by Charles Loewner in 1949 . Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to...
. A uniform inequality for arbitrary 2-complexes with non-free fundamental groups is available, whose proof relies on the Grushko decomposition theorem
Grushko theorem
In the mathematical subject of group theory, the Grushko theorem or the Grushko-Neumann theorem is a theorem stating that the rank of a free product of two groups is equal to the sum of the ranks of the two free factors...
.
See also
- Filling area conjectureFilling area conjectureIn mathematics, in Riemannian geometry, Mikhail Gromov's filling area conjecture asserts that among all possible fillings of the Riemannian circle of length 2π by a surface with the strongly isometric property, the round hemisphere has the least area...
- Gromov's inequalityGromov's inequalityThe following pages deal with inequalities due to Mikhail Gromov:* Bishop–Gromov inequality* Gromov's inequality for complex projective space* Gromov's systolic inequality for essential manifolds* Lévy–Gromov inequality...
- Gromov's inequality for complex projective space
- Loewner's torus inequalityLoewner's torus inequalityIn differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
- Pu's inequality
- Systolic geometry

