
Hall–Janko group
Encyclopedia
In mathematics
, the Hall-Janko group HJ, is a finite
simple
sporadic group
of order
604800. It is also called the second Janko group J2, or the Hall-Janko-Wales group, since it was predicted by Janko
and constructed by Hall
and Wales. It is a subgroup of index
two of the group of automorphisms of the Hall-Janko graph
, leading to a permutation representation of degree 100.
It has a modular representation of dimension six over the field of four elements; if in characteristic
two we have
w2 + w + 1 = 0, then J2 is generated by the two matrices
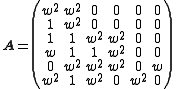
and
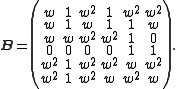
These matrices satisfy the equations
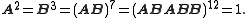
J2 is thus a Hurwitz group, a finite homomorphic image of the (2,3,7) triangle group
.
The matrix representation given above constitutes an embedding into Dickson's
group G2(4)
. There are two conjugacy classes of HJ in G2(4), and they are equivalent under the automorphism on the field F4. Their intersection (the "real" subgroup) is simple of order 6048. G2(4) is in turn isomorphic to a subgroup of the Conway group
Co1.
J2 is the only one of the 4 Janko group
s that is a section of the Monster group
; it is thus part of what Robert Griess calls the Happy Family. Since it is also found in the Conway group Co1, it is therefore part of the second generation of the Happy Family.
Griess relates [p. 123] how Marshall Hall, as editor of The Journal of Algebra
, received a very short paper entitled "A simple group of order 604801." Yes, 604801 is prime.
J2 has 9 conjugacy classes of maximal subgroup
s. Some are here described in terms of action on the Hall-Janko graph.
Janko predicted both J2 and J3
as simple groups having 21+4:A5 as a centralizer of an involution.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hall-Janko group HJ, is a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
604800. It is also called the second Janko group J2, or the Hall-Janko-Wales group, since it was predicted by Janko
Zvonimir Janko
Zvonimir Janko is a Croatian mathematician who is the eponym of the Janko groups, sporadic simple groups in group theory.Janko was born in Bjelovar, Croatia. He studied at the University of Zagreb where he received Ph.D. in 1960. He then taught physics at a high school in Široki Brijeg in Bosnia...
and constructed by Hall
Marshall Hall (mathematician)
Marshall Hall, Jr. was an American mathematician who made contributions to group theory and combinatorics.- Career :...
and Wales. It is a subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
two of the group of automorphisms of the Hall-Janko graph
Hall-Janko graph
In the mathematical field of graph theory, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular undirected graph with 100 vertices and 1800 edges....
, leading to a permutation representation of degree 100.
It has a modular representation of dimension six over the field of four elements; if in characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
two we have
w2 + w + 1 = 0, then J2 is generated by the two matrices
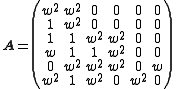
and
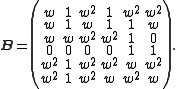
These matrices satisfy the equations
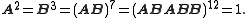
J2 is thus a Hurwitz group, a finite homomorphic image of the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
.
The matrix representation given above constitutes an embedding into Dickson's
Leonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
group G2(4)
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
. There are two conjugacy classes of HJ in G2(4), and they are equivalent under the automorphism on the field F4. Their intersection (the "real" subgroup) is simple of order 6048. G2(4) is in turn isomorphic to a subgroup of the Conway group
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
Co1.
J2 is the only one of the 4 Janko group
Janko group
In mathematics, a Janko group is one of the four sporadic simple groups named for Zvonimir Janko. Janko constructed the first Janko group J1 in 1965. At the same time, Janko also predicted the existence of J2 and J3. In 1976, he suggested the existence of J4...
s that is a section of the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
; it is thus part of what Robert Griess calls the Happy Family. Since it is also found in the Conway group Co1, it is therefore part of the second generation of the Happy Family.
Griess relates [p. 123] how Marshall Hall, as editor of The Journal of Algebra
Journal of Algebra
Journal of Algebra is a leading international mathematical research journal in algebra. An imprint of Academic Press, it is presently published by Elsevier. Journal of Algebra was founded by Graham Higman, who was its editor from 1964 to 1984. From 1985 until 2000, Walter Feit served as its...
, received a very short paper entitled "A simple group of order 604801." Yes, 604801 is prime.
J2 has 9 conjugacy classes of maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
s. Some are here described in terms of action on the Hall-Janko graph.
- U3(3) order 6048 - one-point stabilizer, with orbits of 36 and 63
- Simple, containing 36 simple subgroups of order 168 and 63 involutions, all conjugate, each moving 80 points. A given involution is found in 12 168-subgroups, thus fixes them under conjugacy. Its centralizer has structure 4.S4, which contains 6 additional involutions.
- 3.PGL(2,9) order 2160 - has a subquotient A6
- 21+4:A5 order 1920 - centralizer of involution moving 80 points
- 22+4:(3 × S3) order 1152
- A4 × A5 order 720
- Containing 22 × A5 (order 240), centralizer of 3 involutions each moving 100 points
- A5 × D10 order 600
- PGL(2,7) order 336
- 52:D12 order 300
- A5 order 60
Janko predicted both J2 and J3
Janko group J3
In mathematics, the third Janko group J3, also known as the Higman-Janko-McKay group, is a finite simple sporadic group of order 50232960. Evidence for its existence was uncovered by , and it was shown to exist by...
as simple groups having 21+4:A5 as a centralizer of an involution.
Number of elements of each order
The maximum order of any element is 15. As permutations, elements act on the 100 vertices of the Hall-Janko graph.| Order | No. elements | Cycle structure and conjugacy |
|---|---|---|
| 1 = 1 | 1 = 1 | 1 class |
| 2 = 2 | 315 = 32 · 5 · 7 | 240, 1 class |
| 2520 = 23 · 32 · 5 · 7 | 250, 1 class | |
| 3 = 3 | 560 = 24 · 5 · 7 | 330, 1 class |
| 16800 = 25 · 3 · 52 · 7 | 332, 1 class | |
| 4 = 22 | 6300 = 22 · 32 · 52 · 7 | 26420, 1 class |
| 5 = 5 | 4032 = 26 · 32 · 7 | 520, 2 classes, power equivalent |
| 24192 = 27 · 33 · 7 | 520, 2 classes, power equivalent | |
| 6 = 2 · 3 | 25200 = 24 · 32 · 52 · 7 | 2436612, 1 class |
| 50400 = 25 · 32 · 52 · 7 | 22616, 1 class | |
| 7 = 7 | 86400 = 27 · 33 · 52 | 714, 1 class |
| 8 = 23 | 75600 = 24 · 33 · 52 · 7 | 2343810, 1 class |
| 10 = 2 · 5 | 60480 = 26 · 33 · 5 · 7 | 1010, 2 classes, power equivalent |
| 120960 = 27 · 33 · 5 · 7 | 54108, 2 classes, power equivalent | |
| 12 = 22 · 3 | 50400 = 25 · 32 · 52 · 7 | 324262126, 1 class |
| 15 = 3 · 5 | 80640 = 28 · 32 · 5 · 7 | 52156, 2 classes, power equivalent |

