Harish-Chandra homomorphism
Encyclopedia
In mathematics
, the Harish-Chandra isomorphism, introduced by ,
is an isomorphism
of commutative rings constructed in the theory of Lie algebra
s. The isomorphism maps the center
Z(U(g)) of the universal enveloping algebra
U(g) of a reductive Lie algebra g to the elements S(h)W of the symmetric algebra
S(h) of a Cartan subalgebra h that are invariant under the Weyl group
W.
in n variables (see Chevalley–Shephard–Todd theorem
for a more general statement). Therefore, the center of the universal enveloping algebra of a reductive Lie algebra is a polynomial algebra. The degrees of the generators are the degrees of the fundamental invariants given in the following table.
For example, the center of the universal enveloping algebra of G2 is a polynomial algebra on generators of degrees 2 and 6.
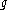be a semisimple Lie algebra, 
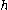its Cartan subalgebra and 
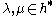be two elements of the weight space and assume that a set of positive roots 
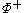have been fixed. Let 
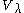, resp. 
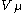be highest weight modules with highest weight 
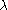, resp. 
.
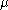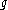-modules 
and 
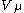
are representations of the universal enveloping algebra
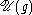and its center
acts on the modules by scalar multiplication (this follows from the fact that the modules are generated by a highest weight vector). So, for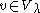
and 
,
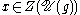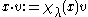
and similarly for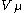
.
The functions
are homomorphims to scalars called central characters.
, the characters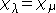 
if and only if 
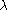and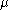 
are on the same orbit of the Weyl group
of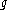
under the affine action (corresponding to the choice of the positive roots 
).
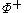Another closely related formulation is that
the Harish-Chandra homomorphism
from the centrum of the universal enveloping algebra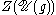
to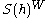 
(invariant polynomials over the Cartan subalgebra fixed by the affine action of the Weyl group) is an isomorphism
.
Further, it is a necessary condition for the existence of a nonzero homomorphism of some highest weight moules (a homomorphism of such modules preserves central character). A simple consequence is that for Verma module
s or generalized Verma module
s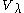
with highest weight 
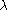, there exist only finitely many weights 
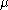such that
a nonzero homomorphism
exists.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Harish-Chandra isomorphism, introduced by ,
is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of commutative rings constructed in the theory of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. The isomorphism maps the center
Center (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
Z(U(g)) of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
U(g) of a reductive Lie algebra g to the elements S(h)W of the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
S(h) of a Cartan subalgebra h that are invariant under the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
W.
Fundamental invariants
Let n be the rank of g, which is the dimension of the Cartan subalgebra h. H. S. M. Coxeter observed that S(h)W is a polynomial algebraPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in n variables (see Chevalley–Shephard–Todd theorem
Chevalley–Shephard–Todd theorem
In mathematics, the Chevalley–Shephard–Todd theorem in invariant theory of finite groups states that the ring of invariants of a finite group acting on a complex vector space is a polynomial ring if and only if the group is generated by pseudoreflections. In the case of subgroups of the complex...
for a more general statement). Therefore, the center of the universal enveloping algebra of a reductive Lie algebra is a polynomial algebra. The degrees of the generators are the degrees of the fundamental invariants given in the following table.
| Lie algebra | Coxeter number Coxeter number In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group, hence also of a root system or its Weyl group. It is named after H.S.M. Coxeter.-Definitions:... h | Dual Coxeter number | Degrees of fundamental invariants |
|---|---|---|---|
| R | 0 | 0 | 1 |
| An | n + 1 | n + 1 | 2, 3, 4, ..., n + 1 |
| Bn | 2n | 2n − 1 | 2, 4, 6, ..., 2n |
| Cn | 2n | n + 1 | 2, 4, 6, ..., 2n |
| Dn | 2n − 2 | 2n − 2 | n; 2, 4, 6, ..., 2n − 2 |
| E6 | 12 | 12 | 2, 5, 6, 8, 9, 12 |
| E7 | 18 | 18 | 2, 6, 8, 10, 12, 14, 18 |
| E8 | 30 | 30 | 2, 8, 12, 14, 18, 20, 24, 30 |
| F4 | 12 | 9 | 2, 6, 8, 12 |
| G2 | 6 | 4 | 2, 6 |
For example, the center of the universal enveloping algebra of G2 is a polynomial algebra on generators of degrees 2 and 6.
Examples
- If g is the Lie algebra sl2(R), then the center of the universal enveloping algebra is generated by the Casimir invariantCasimir invariantIn mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
of degree 2, and the ring of invariants of the Weyl group is also generated by an element of degree 2.
Introduction and setting
Let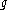 be a semisimple Lie algebra, 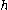its Cartan subalgebra and 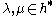be two elements of the weight space and assume that a set of positive roots 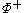have been fixed. Let 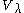, resp. 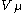be highest weight modules with highest weight 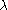, resp. 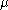.Central characters
The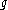-modules and 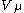are representations of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
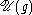and its centerCenter (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
acts on the modules by scalar multiplication (this follows from the fact that the modules are generated by a highest weight vector). So, for
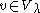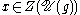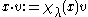
and ,and similarly for
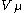.The functions
are homomorphims to scalars called central characters.Statement of Harish-Chandra theorem
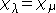For any, the characters if and only if 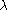and 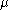are on the same orbit of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of
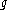under the affine action (corresponding to the choice of the positive roots 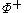).Another closely related formulation is that
the Harish-Chandra homomorphism
Harish-Chandra homomorphism
In mathematics, the Harish-Chandra isomorphism, introduced by ,is an isomorphism of commutative rings constructed in the theory of Lie algebras...
from the centrum of the universal enveloping algebra
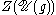to 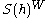(invariant polynomials over the Cartan subalgebra fixed by the affine action of the Weyl group) is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
Applications
The theorem may be used to obtain a simple algebraic proof of Weyl's character formula for finite dimensional representations.Further, it is a necessary condition for the existence of a nonzero homomorphism of some highest weight moules (a homomorphism of such modules preserves central character). A simple consequence is that for Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
s or generalized Verma module
Generalized Verma module
In mathematics, generalized Verma modules are a generalization of a Verma module, and are objects in the representation theory of Lie algebras. They were studied originally by James Lepowsky in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to...
s
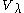with highest weight 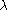, there exist only finitely many weights 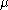such thata nonzero homomorphism
exists.See also
- Translation functorTranslation functorIn mathematical representation theory, a translation functor is a functor taking representations of a Lie algebra to representations with a possibly different central character. Translation functors were introduced independently by and...
- Universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
- Infinitesimal characterInfinitesimal characterIn mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...