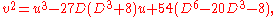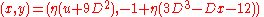Hessian curve
Encyclopedia
In geometry
, the Hessian curve is a plane curve
similar to folium of Descartes
. It is named after the German mathematician Otto Hesse
.
This curve was suggested for application in elliptic curve cryptography
, because arithmetic in this curve representation is faster and needs less memory than arithmetic in standard Weierstrass form.
be a field
and let E denote an elliptic curve
in Weierstrass form over
. Then the following curve can be obtained:
where the curve has discriminant
and (0,0) has order 3. Before proving this, note that if the characteristic
of
, say q, is 2 modulo 3, then the curve has 3 points of order 3; and if q is 1 modulo 3, there are 8 points of order 3.
To prove that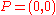
has order 3, it is sufficient to show that 
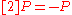using the elliptic curve group law.
(i) Compute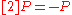
: if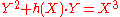 
is the given curve and 
the point, then 
.
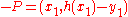So, in this case, since
, then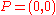 
.
(ii) Compute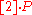
: it can be done using the tangent and chord method, that is, first construct the line through the general point 
and find the other intersection point with the curve.
Let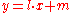
be the tangent to the curve at 
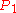. Now, to find the points of intersection between the curve and the line, replace every 
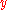by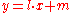 
in the curve:
iff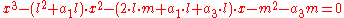 
The roots of this equation are the x-coordinates of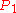
and 
, so:
Then comparing the coefficients:
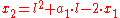and 
(
and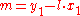 
).
Note that
are known and by the implicit function theorem
(which is the slope
of the line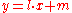
). Then, 
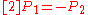and [2]P would be known. This is a general method to compute 
.
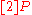So applying it to P=(0,0):
since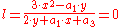
(note 
cannot be zero, otherwise the denominator would vanish at 
and the curve would be singular),
then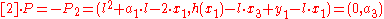
where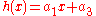 
Thus,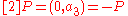
, that is (0,0) has order 3 over 
.
Now, to obtain the Hessian curve, it is necessary to do the following transformation
:
First let
denote a root
of the polynomial T3 − δT2 + δ2T/3 + a3
2 = 0.
where
is determined from the formula:
=1/3((-27a3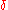
2)1/3+
)
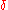Note that if
has characteristic
q ≡ 2 (mod 3), then every element of
has a unique cube root; otherwise, it is necessary to consider an extension field of K.
Now by defining the following value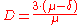
another curve, C, is obtained, that is birationally equivalent
to E:
: 
which is called cubic Hessian form (in projective coordinates
)
: 
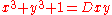
in the affine plane ( satisfying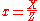
and 
).
Furthermore, D3≠1 (otherwise, the curve would be singular
)
Starting from the Hessian curve, a birationally equivalent Weierstrass equation is given by
under the transformations:
and
where:
=[6(D3-1)(v+9D3-3Du-36)]/[(u+9D2)3+(3Dd-Du-12)3]
=[12(D3-1)]/[Dx+y+1]
In general, the group law is defined in the following way: if three points lie in the same line then they sum up to zero. So, by this property, the group laws are different for every curve.
In this case, the correct way is to use the Cauchy-Desboves´ formulas, obtaining the point at infinity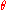
= ( 1 : -1: 0), that is, the neutral element
(the inverse of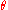
is 
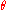again).
Let P=(x1,y1) be a point on the curve. The line
contains the point 
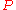and the point at infinity 
.
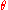Therefore, -P is the third point of the intersection of this line with the curve. Intersecting the elliptic curve with the line, the following condition is obtained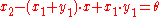
Since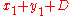
is non zero (because 
is distinct to 1), the x-coordinate of 
is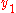 
and the y-coordinate of 
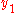is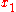 
, i.e. , 
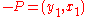or in projective coordinates 
.
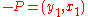In some application of elliptic curve cryptography
and the elliptic curve method of factorization (ECM
) it is necessary to compute the scalar multiplications of P, say [n]P for some integer
n, and they are based on the double-and-add method
; these operations need the addition and dobling formulas.
Doubling
Now, if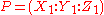
is a point on the elliptic curve, it is possible to define a "doubling" operation using Cauchy-Desboves´ formulae:
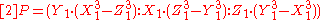
Addition
In the same way, for two different points, say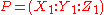
and 
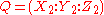, it is possible to define the addition formula. Let 
denote the sum of these points, 
, then its coordinates are given by:
Proposition. Let P=(X,Y,Z) be a point on a Hessian elliptic curve E(K). Then: 2(X:Y:Z) = (Z:X:Y) + (Y:Z:X) (2).
Furthermore, we have (Z:X:Y)≠(Y:Z:X).
Finally, contrary to other parameterizations
, there is no subtraction to compute the negation of a point. Hence, this addition algorithm can also be used for subtracting two points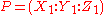
and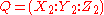 
on a Hessian elliptic curve:
( X1:Y1:Z1) - ( X2:Y2:Z2) = ( X1:Y1:Z1) + (Y2:X2:Z2) (3)
To sum up, by adapting the order of the inputs according to equation (2) or (3), the addition algorithm presented above can be used indifferently for:
Adding 2 (diff.) points, Doubling a point and Subtracting 2 points with only 12 multiplications and 7 auxiliary variables including the 3 result variables. Before the invention of Edwards curves,
these results represent the fastest known method for implementing the elliptic curve scalar multiplication towards resistance against side-channel attacks.
For some algorithms protection against side-channel attacks is not necessary. So, for these doublings can be faster. Since there are many algorithms, only the best for the addition and doubling formulas is given here, with one example for each one:
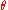. Assuming that Z1=Z2=1 then the algorithm is given by:
A = X1 Y2
B = Y1 X2
The cost needed is 8 multiplications and 3 additions readdition cost of 7 multiplications and 3 additions, depending on the first point.
Example
Given the following points in the curve for d=-1 P1=(1:0:-1) and P2=(0:-1:1), then if P3=P1+P2 we have:
Then: P3=(-1:-1:0)
The cost of this algorithm is three multiplications + three squarings + 11 additions + 3×2.
Example
If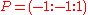
is a point over the Hessian curve with parameter d=-1, then the coordinates of 
are given by:
X=(2.(-1)-2)(-1+1+1)=-4
Y=(-4-2.(-1))((-1)+1+1)=-2
Z=(-1-(-1))((-4)+2.2)=0
That is,
http://hyperelliptic.org/EFD/g1p/auto-hessian-extended.html#addition-add-20080225-hwcd
and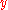 
are represented by 
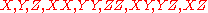satisfying the following equations:
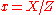
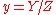
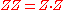
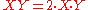
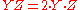
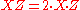
Twisted Hessian curves
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Hessian curve is a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
similar to folium of Descartes
Folium of Descartes
In geometry, the Folium of Descartes is an algebraic curve defined by the equationx^3 + y^3 - 3 a x y = 0 \,.It forms a loop in the first quadrant with a double point at the origin and asymptotex + y + a = 0 \,.It is symmetrical about y = x....
. It is named after the German mathematician Otto Hesse
Otto Hesse
Ludwig Otto Hesse was a German mathematician. Hesse was born in Königsberg, Prussia, and died in Munich, Bavaria. He worked on algebraic invariants...
.
This curve was suggested for application in elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
, because arithmetic in this curve representation is faster and needs less memory than arithmetic in standard Weierstrass form.
Definition
Let be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and let E denote an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
in Weierstrass form over
. Then the following curve can be obtained:where the curve has discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
and (0,0) has order 3. Before proving this, note that if the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of
, say q, is 2 modulo 3, then the curve has 3 points of order 3; and if q is 1 modulo 3, there are 8 points of order 3.To prove that
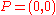has order 3, it is sufficient to show that 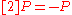using the elliptic curve group law.(i) Compute
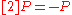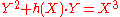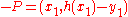: if is the given curve and the point, then .So, in this case, since
, then 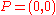.(ii) Compute
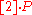: it can be done using the tangent and chord method, that is, first construct the line through the general point and find the other intersection point with the curve.Let
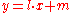be the tangent to the curve at 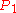. Now, to find the points of intersection between the curve and the line, replace ever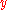y by 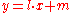in the curve: iff 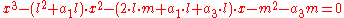The roots of this equation are the x-coordinates of
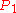and , so:Then comparing the coefficients:
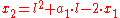and ( and 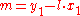).Note that
are known and by the implicit function theoremImplicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
(which is the slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the line
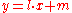). Then, 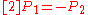and [2]P would be known. This is a general method to compute 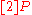.So applying it to P=(0,0):
since
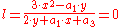(note cannot be zero, otherwise the denominator would vanish at and the curve would be singular),then
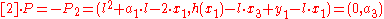where 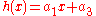Thus,
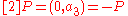, that is (0,0) has order 3 over .Now, to obtain the Hessian curve, it is necessary to do the following transformation
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
:
First let
denote a rootEquation solving
In mathematics, to solve an equation is to find what values fulfill a condition stated in the form of an equation . These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled...
of the polynomial T3 − δT2 + δ2T/3 + a3
2 = 0.where
is determined from the formula:=1/3((-27a3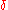2)1/3+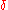)Note that if
has characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
q ≡ 2 (mod 3), then every element of
has a unique cube root; otherwise, it is necessary to consider an extension field of K.Now by defining the following value
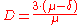another curve, C, is obtained, that is birationally equivalentBirational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
to E:
: which is called cubic Hessian form (in projective coordinates
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
)
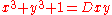
: in the affine plane ( satisfying
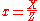and ).Furthermore, D3≠1 (otherwise, the curve would be singular
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
)
Starting from the Hessian curve, a birationally equivalent Weierstrass equation is given by
under the transformations:
and
where:
=[6(D3-1)(v+9D3-3Du-36)]/[(u+9D2)3+(3Dd-Du-12)3]=[12(D3-1)]/[Dx+y+1]Group law
It is interesting to analyze the group law of the elliptic curve, defining the addition and doubling formulas (because the SPA and DPA attacks are based on the running time of these operations). Furthermore, in this case, we only need to use the same procedure to compute the addition, doubling or subtraction of points to get efficient results, as said above.In general, the group law is defined in the following way: if three points lie in the same line then they sum up to zero. So, by this property, the group laws are different for every curve.
In this case, the correct way is to use the Cauchy-Desboves´ formulas, obtaining the point at infinity
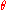= ( 1 : -1: 0), that is, the neutral elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
(the inverse of
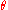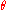is again).Let P=(x1,y1) be a point on the curve. The line
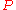contains the point and the point at infinity 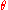.Therefore, -P is the third point of the intersection of this line with the curve. Intersecting the elliptic curve with the line, the following condition is obtained
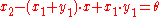
Since
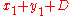is non zero (because is distinct to 1), the x-coordinate of is 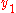and the y-coordinate of 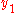is 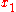, i.e. , 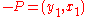or in projective coordinates 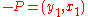.In some application of elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
and the elliptic curve method of factorization (ECM
Lenstra elliptic curve factorization
The Lenstra elliptic curve factorization or the elliptic curve factorization method is a fast, sub-exponential running time algorithm for integer factorization which employs elliptic curves. For general purpose factoring, ECM is the third-fastest known factoring method...
) it is necessary to compute the scalar multiplications of P, say [n]P for some integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, and they are based on the double-and-add method
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
; these operations need the addition and dobling formulas.
Doubling
Now, if
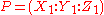is a point on the elliptic curve, it is possible to define a "doubling" operation using Cauchy-Desboves´ formulae: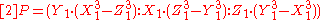Addition
In the same way, for two different points, say
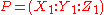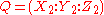and , it is possible to define the addition formula. Let denote the sum of these points, , then its coordinates are given by:Algorithms and examples
There is one algorithm that can be used to add two different points or to double; it is given by Joye and Quisquarter. Then, the following result gives the possibility the obtain the doubling operation by the addition:Proposition. Let P=(X,Y,Z) be a point on a Hessian elliptic curve E(K). Then: 2(X:Y:Z) = (Z:X:Y) + (Y:Z:X) (2).
Furthermore, we have (Z:X:Y)≠(Y:Z:X).
Finally, contrary to other parameterizations
Parametrization
Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....
, there is no subtraction to compute the negation of a point. Hence, this addition algorithm can also be used for subtracting two points
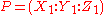and 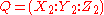on a Hessian elliptic curve:( X1:Y1:Z1) - ( X2:Y2:Z2) = ( X1:Y1:Z1) + (Y2:X2:Z2) (3)
To sum up, by adapting the order of the inputs according to equation (2) or (3), the addition algorithm presented above can be used indifferently for:
Adding 2 (diff.) points, Doubling a point and Subtracting 2 points with only 12 multiplications and 7 auxiliary variables including the 3 result variables. Before the invention of Edwards curves,
these results represent the fastest known method for implementing the elliptic curve scalar multiplication towards resistance against side-channel attacks.
For some algorithms protection against side-channel attacks is not necessary. So, for these doublings can be faster. Since there are many algorithms, only the best for the addition and doubling formulas is given here, with one example for each one:
Addition
Let P1=(X1:Y1:Z1) and P2=(X2:Y2:Z2) be two points distinct to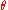. Assuming that Z1=Z2=1 then the algorithm is given by:A = X1 Y2
B = Y1 X2
- X3 = B Y1-Y2 A
- Y3 = X1 A-B X2
- Z3 = Y2 X2-X1 Y1
The cost needed is 8 multiplications and 3 additions readdition cost of 7 multiplications and 3 additions, depending on the first point.
Example
Given the following points in the curve for d=-1 P1=(1:0:-1) and P2=(0:-1:1), then if P3=P1+P2 we have:
- X3=0-1=-1
- Y3=-1-0=-1
- Z3=0-0=0
Then: P3=(-1:-1:0)
Doubling
Let P = (X1 : Y1 : Z1) be a point, then the doubling formula is given by:- A = X12
- B = Y12
- D = A + B
- G = (X1 + Y1)2 − D
- X3 = (2Y1 − G) × (X1 + A + 1)
- Y3 = (G − 2X1) × (Y1 + B + 1)
- Z3 = (X1 − Y1) × (G + 2D)
The cost of this algorithm is three multiplications + three squarings + 11 additions + 3×2.
Example
If
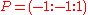is a point over the Hessian curve with parameter d=-1, then the coordinates of are given by:X=(2.(-1)-2)(-1+1+1)=-4
Y=(-4-2.(-1))((-1)+1+1)=-2
Z=(-1-(-1))((-4)+2.2)=0
That is,
Extended coordinates
There is another coordinates system with which a Hessian curve can be represented; these new coordinates are called extended coordinates. They can speed up the addition and doubling. To have more information about operations with the extended coordinates see:http://hyperelliptic.org/EFD/g1p/auto-hessian-extended.html#addition-add-20080225-hwcd
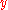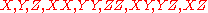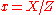
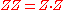
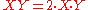
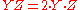
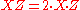
and are represented by satisfying the following equations:See also
For more information about the running-time required in a specific case, see Table of costs of operations in elliptic curvesTable of costs of operations in elliptic curves
This table relates to the computational cost for certain operations used in elliptic curve cryptography, used in practice for strong cryptographic security of a public key system. The columns of the table are labelled by various computational steps...
Twisted Hessian curves
Twisted Hessian curves
In mathematics, the Twisted Hessian curve represents a generalization of Hessian curves; it was introduced in elliptic curve cryptography to speed up the addition and doubling formulas and to have strongly unified arithmetic. In some operations , it is close in speed to Edwards...