
Inverse problem for Lagrangian mechanics
Encyclopedia
In mathematics
, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equation
s can arise as the Euler–Lagrange equations for some Lagrangian
function.
There has been a great deal of activity in the study of this problem since the early 20th century. A notable advance in this field was a 1941 paper by the American
mathematician
Jesse Douglas
, in which he provided necessary and sufficient conditions for the problem to have a solution; these conditions are now known as the Helmholtz conditions, after the German
physicist
Hermann von Helmholtz
.
on n-dimension
al Euclidean space
Rn is as follows. Consider a differentiable path
u : [0, T] → Rn. The action of the path u, denoted S(u), is given by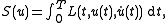
where L is a function of time, position and velocity
known as the Lagrangian. The principle of least action
states that, given an initial state x0 in Rn, the trajectory that the system determined by L will actually follow must be a minimizer of the action functional
S satisfying the initial condition u(0) = x0. Furthermore, the critical point
s (and hence minimizers) of S must satisfy the Euler–Lagrange equations for S:
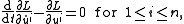
where the upper indices i denote the components of u = (u1, ..., un).
In the classical case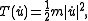
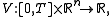
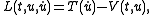
the Euler–Lagrange equations are the second-order ordinary differential equations better known as Newton's laws of motion
: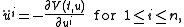
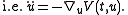
The inverse problem of Lagrangian mechanics is as follows: given a system of second-order ordinary differential equations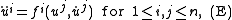
that holds for times 0 ≤ t ≤ T, does there exist a Lagrangian L : [0, T] × Rn × Rn → R for which these ordinary differential equations (E) are the Euler–Lagrange equations? In general, this problem is posed not on Euclidean space Rn, but on an n-dimensional manifold
M, and the Lagrangian is a function L : [0, T] × TM → R, where TM denotes the tangent bundle
of M.
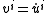
and define a collection of n2 functions Φji by
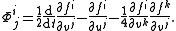
Theorem. (Douglas 1941) There exists a Lagrangian L : [0, T] × TM → R such that the equations (E) are its Euler–Lagrange equations if and only if
there exists a non-singular symmetric matrix g with entries gij depending on both u and v satisfying the following three Helmholtz conditions:
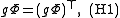
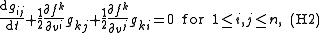
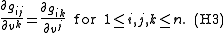
(The Einstein summation convention is in use for the repeated indices.)
connection
on a Lie group
), this condition is satisfied.
The final and most difficult step is to solve equation (H3), called the closure conditions since (H3) is the condition that the differential 1-form
gi is a closed form
for each i. The reason why this is so daunting is that (H3) constitutes a large system of coupled partial differential equations: for n degrees of freedom, (H3) constitutes a system of
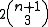
partial differential equations in the 2n independent variables that are the components gij of g, where
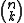
denotes the binomial coefficient
. In order to construct the most general possible Lagrangian, one must solve this huge system!
Fortunately, there are some auxiliary conditions that can be imposed in order to help in solving the Helmholtz conditions. First, (H1) is a purely algebraic condition on the unknown matrix g. Auxiliary algebraic conditions on g can be given as follows: define functions
by
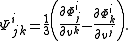
The auxiliary condition on g is then
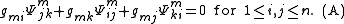
In fact, the equations (H2) and (A) are just the first in an infinite hierarchy of similar algebraic conditions. In the case of a parallel connection (such as the canonical connection on a Lie group), the higher order conditions are always satisfied, so only (H2) and (A) are of interest. Note that (A) comprises
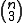
conditions whereas (H1) comprises
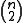
conditions. Thus, it is possible that (H1) and (A) together imply that the Lagrangian function is singular. As of 2006, there is no general theorem to circumvent this difficulty in arbitrary dimension, although certain special cases have been resolved.
A second avenue of attack is to see whether the system (E) admits a submersion onto a lower-dimensional system and to try to "lift" a Lagrangian for the lower-dimensional system up to the higher-dimensional one. This is not really an attempt to solve the Helmholtz conditions so much as it is an attempt to construct a Lagrangian and then show that its Euler–Lagrange equations are indeed the system (E).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s can arise as the Euler–Lagrange equations for some Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
function.
There has been a great deal of activity in the study of this problem since the early 20th century. A notable advance in this field was a 1941 paper by the American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Jesse Douglas
Jesse Douglas
Jesse Douglas was an American mathematician. He was born in New York and attended Columbia College of Columbia University from 1920–1924. Douglas was one of two winners of the first Fields Medals, awarded in 1936. He was honored for solving, in 1930, the problem of Plateau, which asks whether a...
, in which he provided necessary and sufficient conditions for the problem to have a solution; these conditions are now known as the Helmholtz conditions, after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Hermann von Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
.
Background and statement of the problem
The usual set-up of Lagrangian mechanicsLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
on n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is as follows. Consider a differentiable path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
u : [0, T] → Rn. The action of the path u, denoted S(u), is given by
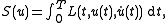
where L is a function of time, position and velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
known as the Lagrangian. The principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
states that, given an initial state x0 in Rn, the trajectory that the system determined by L will actually follow must be a minimizer of the action functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
S satisfying the initial condition u(0) = x0. Furthermore, the critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s (and hence minimizers) of S must satisfy the Euler–Lagrange equations for S:
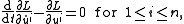
where the upper indices i denote the components of u = (u1, ..., un).
In the classical case
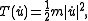
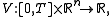
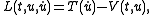
the Euler–Lagrange equations are the second-order ordinary differential equations better known as Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
:
The inverse problem of Lagrangian mechanics is as follows: given a system of second-order ordinary differential equations
that holds for times 0 ≤ t ≤ T, does there exist a Lagrangian L : [0, T] × Rn × Rn → R for which these ordinary differential equations (E) are the Euler–Lagrange equations? In general, this problem is posed not on Euclidean space Rn, but on an n-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M, and the Lagrangian is a function L : [0, T] × TM → R, where TM denotes the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M.
Douglas' theorem and the Helmholtz conditions
To simplify the notation, let
and define a collection of n2 functions Φji by
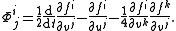
Theorem. (Douglas 1941) There exists a Lagrangian L : [0, T] × TM → R such that the equations (E) are its Euler–Lagrange equations if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists a non-singular symmetric matrix g with entries gij depending on both u and v satisfying the following three Helmholtz conditions:
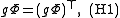
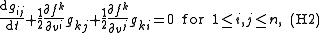
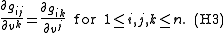
(The Einstein summation convention is in use for the repeated indices.)
Applying Douglas' theorem
At first glance, solving the Helmholtz equations (H1)–(H3) seems to be an extremely difficult task. Condition (H1) is the easiest to solve: it is always possible to find a g that satisfies (H1), and it alone will not imply that the Lagrangian is singular. Equation (H2) is a system of ordinary differential equations: the usual theorems on the existence and uniqueness of solutions to ordinary differential equations imply that it is, in principle, possible to solve (H2). Integration does not yield additional constants but instead first integrals of the system (E), so this step becomes difficult in practice unless (E) has enough explicit first integrals. In certain well-behaved cases (e.g. the geodesic flow for the canonicalCanonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
), this condition is satisfied.
The final and most difficult step is to solve equation (H3), called the closure conditions since (H3) is the condition that the differential 1-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
gi is a closed form
Closed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
for each i. The reason why this is so daunting is that (H3) constitutes a large system of coupled partial differential equations: for n degrees of freedom, (H3) constitutes a system of
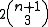
partial differential equations in the 2n independent variables that are the components gij of g, where
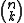
denotes the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. In order to construct the most general possible Lagrangian, one must solve this huge system!
Fortunately, there are some auxiliary conditions that can be imposed in order to help in solving the Helmholtz conditions. First, (H1) is a purely algebraic condition on the unknown matrix g. Auxiliary algebraic conditions on g can be given as follows: define functions
- Ψjki
by
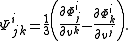
The auxiliary condition on g is then
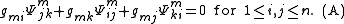
In fact, the equations (H2) and (A) are just the first in an infinite hierarchy of similar algebraic conditions. In the case of a parallel connection (such as the canonical connection on a Lie group), the higher order conditions are always satisfied, so only (H2) and (A) are of interest. Note that (A) comprises
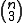
conditions whereas (H1) comprises
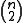
conditions. Thus, it is possible that (H1) and (A) together imply that the Lagrangian function is singular. As of 2006, there is no general theorem to circumvent this difficulty in arbitrary dimension, although certain special cases have been resolved.
A second avenue of attack is to see whether the system (E) admits a submersion onto a lower-dimensional system and to try to "lift" a Lagrangian for the lower-dimensional system up to the higher-dimensional one. This is not really an attempt to solve the Helmholtz conditions so much as it is an attempt to construct a Lagrangian and then show that its Euler–Lagrange equations are indeed the system (E).

