Inversive ring geometry
Encyclopedia
In mathematics
, inversive ring geometry is the extension of the concepts of projective line
, homogeneous coordinates
, projective transformations, and cross-ratio
to the context of associative ring
s, concepts usually built upon rings that happen to be fields
.
One begins with ordered pairs (a, b) in A×A where A is an (associative) ring with 1. Let U be the group of units of the ring. When there is g in U such that
= (u, v),
then we write
~ (a, b).
In other words, we identify orbits under the action of U, and ~ is the corresponding equivalence relation
.
Two elements of a ring are relatively prime if the ideal
in A that they generate is the whole of A. The projective line over A is the set of equivalence classes for ~ on pairs of relatively prime elements :
):
on A is generated by the mappings x → x + c and x → x u, u
∈ U.
The group of projectivities on P(A) extends the affine group by including reciprocation x → x−1 as follows:
Represent translations by U(x, 1)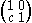
= U(x + c, 1).
Represent "rotations" by U(x, 1)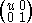
= U(x u, 1).
Include reciprocation
with U(x, y)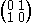
= U(y, x).
Note that if u ∈ U, then U(1, u) = U(u−1, 1) = U(u, 1)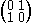
.
Here the elements of P(A) present themselves as row vectors for matrix transformation; this way subsequent transformations appear on the right, consistent with reading order.
Composition of mappings is represented by matrix multiplication where the matrices are of
the 2 × 2 type exhibited with entries taken from the ring A. Call the set of them M(A, 2) so
the group of projectivities G(A) ⊂ M(A, 2).
For instance, in G(A) one finds the projectivity
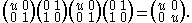
Its action is U(x, 1)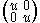
= U(xu, u) = U(u−1 xu, 1).
Thus the inner automorphism
x → u−1 x u of the group of units U ⊂ A arises as a projectivity on P(A) by an element of G(A). For example, when A is the ring of quaternion
s then one obtains rotations of 3-space
.
In case A is the ring of biquaternions, which has two conjugations, projectivities include the mappings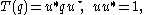
which provide a group representation
for the Lorentz group
of special relativity
.
.
Suppose p, q, r ∈ A with
When these inverses t and v exist we say "p, q, and r are
separated sufficiently". Now look at
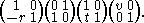
The first two factors put r at U(1, 0) = ∞ where it stays. The third factor moves t, the image of p
under the first two factors, to U(0, 1), or zero in the canonical embedding. Finally, the
fourth factor has traced q through the first three factors and formation of the rotation with
v places U(q, 1) at U(1, 1). Thus the composition displayed places the triple p,q,r at the
triple 0,1,∞. Evidently it is the unique such projectivity considering the pivotal use of fixed points
of generators to bring the triple to 0,1,∞.
If s and t are two sufficiently separated triples then they correspond to projectivities g and
h respectively which map each of s and t to (0,1,∞). Thus the projectivity h−1 o g maps s to t .
Denote by (x,p,q,r) the image of x under the projectivity determined by p,q,r as above. This function f(x) is the cross-ratio determined by p,q,r ∈ A. The uniqueness of this function implies that when a single projectivity g ∈ G(A) is used to form another triple g(p), g(q), g(r) from the first one, then the new cross-ratio function h must agree with f o g. Hence h o g−1 = f so that
(g(x), g(p),
g(q), g(r) ) = (x, p, q, r).
investigated the Möbius transformations between his book Baricentric Calculus(1827) and his 1855 paper "Theorie der Kreisverwandtschaft in rein geometrischer Darstellung". Karl Wilhelm Feuerbach
and Julius Plücker
are also credited with originating the use of homogeneous coordinates. Eduard Study
in 1898, and Élie Cartan
in 1908, wrote articles on hypercomplex numbers for German and French Encyclopedias of Mathematics, respectively, where they use these arithmetics to define linear-fractional transformations in imitation of those of Mobius. In 1902 Theodore Vahlen contributed a short but well-referenced paper exploring some linear-fractional transformations of a Clifford algebra
. The ring of dual numbers D gave Josef Grünwald opportunity to exhibit P(D) in 1906. Corrado Segre
(1912) continued the development with that ring.
Arthur Conway
, one of the early adopters of relativity via biquaternion transformations, considered the quaternion-multiplicative-inverse transformation in his 1911 relativity study (see page 9). In 1947 some elements of inversive quaternion geometry were described by P.G. Gormley in his paper "Stereographic projection and the linear fractional group of transformations of quaternions". In 1968 Isaak Yaglom
's Complex Numbers in Geometry appeared in English, translated from Russian. There he uses P(D) to describe line geometry in the Euclidean plane and P(M) to describe it for Lobachevski's plane. Yaglom's text A Simple Non-Euclidean Geometry appeared in English in 1979. There in pages 174 to 200 he develops Minkowskian geometry and describes P(M) as the "inversive Minkowski plane". The Russian original of Yaglom's text was published in 1969. Between the two editions, Walter Benz
(1973) published his book which included the homogeneous coordinates taken from M.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, inversive ring geometry is the extension of the concepts of projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
, homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, projective transformations, and cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
to the context of associative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, concepts usually built upon rings that happen to be fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
One begins with ordered pairs (a, b) in A×A where A is an (associative) ring with 1. Let U be the group of units of the ring. When there is g in U such that
= (u, v),
then we write
~ (a, b).
In other words, we identify orbits under the action of U, and ~ is the corresponding equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
Two elements of a ring are relatively prime if the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in A that they generate is the whole of A. The projective line over A is the set of equivalence classes for ~ on pairs of relatively prime elements :
- P(A) = { U(a, b) ∈ A × A / ~ : A a + A b = A }.
Examples
Examples with topological descriptions (≈ denotes homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
):
- A = C complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane : P(C) ≈ S2 = Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity... - A = H quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ring : P(H) ≈ S4 = One-point compactificationCompactification (mathematics)In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An... - A = D dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
plane : P(D) = D ∪ { U(1, x n): x ∈ R}, nn = 0 - A = M split-complexSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
plane : P(M) ≈ hyperboloid of one sheet.
Affine and projective groups
The affine groupAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
on A is generated by the mappings x → x + c and x → x u, u
∈ U.
The group of projectivities on P(A) extends the affine group by including reciprocation x → x−1 as follows:
Represent translations by U(x, 1)
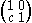= U(x + c, 1).Represent "rotations" by U(x, 1)
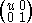= U(x u, 1).Include reciprocation
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
with U(x, y)
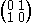= U(y, x).Note that if u ∈ U, then U(1, u) = U(u−1, 1) = U(u, 1)
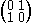.Here the elements of P(A) present themselves as row vectors for matrix transformation; this way subsequent transformations appear on the right, consistent with reading order.
Composition of mappings is represented by matrix multiplication where the matrices are of
the 2 × 2 type exhibited with entries taken from the ring A. Call the set of them M(A, 2) so
the group of projectivities G(A) ⊂ M(A, 2).
For instance, in G(A) one finds the projectivity
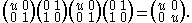
Its action is U(x, 1)
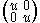= U(xu, u) = U(u−1 xu, 1).Thus the inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
x → u−1 x u of the group of units U ⊂ A arises as a projectivity on P(A) by an element of G(A). For example, when A is the ring of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s then one obtains rotations of 3-space
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
.
In case A is the ring of biquaternions, which has two conjugations, projectivities include the mappings
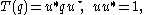which provide a group representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
for the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Cross-ratio theorems
Here we consider existence, uniqueness, matching triples, and invarianceInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
.
Suppose p, q, r ∈ A with
- t = (r – p)−1 and v = (t + (q – r)−1)−1.
When these inverses t and v exist we say "p, q, and r are
separated sufficiently". Now look at
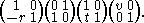
The first two factors put r at U(1, 0) = ∞ where it stays. The third factor moves t, the image of p
under the first two factors, to U(0, 1), or zero in the canonical embedding. Finally, the
fourth factor has traced q through the first three factors and formation of the rotation with
v places U(q, 1) at U(1, 1). Thus the composition displayed places the triple p,q,r at the
triple 0,1,∞. Evidently it is the unique such projectivity considering the pivotal use of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of generators to bring the triple to 0,1,∞.
If s and t are two sufficiently separated triples then they correspond to projectivities g and
h respectively which map each of s and t to (0,1,∞). Thus the projectivity h−1 o g maps s to t .
Denote by (x,p,q,r) the image of x under the projectivity determined by p,q,r as above. This function f(x) is the cross-ratio determined by p,q,r ∈ A. The uniqueness of this function implies that when a single projectivity g ∈ G(A) is used to form another triple g(p), g(q), g(r) from the first one, then the new cross-ratio function h must agree with f o g. Hence h o g−1 = f so that
g(q), g(r) ) = (x, p, q, r).
History
August Ferdinand MöbiusAugust Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
investigated the Möbius transformations between his book Baricentric Calculus(1827) and his 1855 paper "Theorie der Kreisverwandtschaft in rein geometrischer Darstellung". Karl Wilhelm Feuerbach
Karl Wilhelm Feuerbach
Karl Wilhelm von Feuerbach was a German geometer and the son of legal scholar Paul Johann Anselm Ritter von Feuerbach, and the brother of philosopher Ludwig Feuerbach. After receiving his doctorate at age 22, he became a professor of mathematics at the Gymnasium at Erlangen...
and Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
are also credited with originating the use of homogeneous coordinates. Eduard Study
Eduard Study
Eduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
in 1898, and Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
in 1908, wrote articles on hypercomplex numbers for German and French Encyclopedias of Mathematics, respectively, where they use these arithmetics to define linear-fractional transformations in imitation of those of Mobius. In 1902 Theodore Vahlen contributed a short but well-referenced paper exploring some linear-fractional transformations of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. The ring of dual numbers D gave Josef Grünwald opportunity to exhibit P(D) in 1906. Corrado Segre
Corrado Segre
Corrado Segre was an Italian mathematician who is remembered today as a major contributor to the early development of algebraic geometry....
(1912) continued the development with that ring.
Arthur Conway
Arthur Conway
Arthur Joseph Conway was an English cricketer: a right-handed batsman and right-arm fast bowler Arthur Joseph Conway (1 April 1885 – 29 October 1954) was an English cricketer: a right-handed batsman and right-arm fast bowler Arthur Joseph Conway (1 April 1885 – 29 October 1954) was an...
, one of the early adopters of relativity via biquaternion transformations, considered the quaternion-multiplicative-inverse transformation in his 1911 relativity study (see page 9). In 1947 some elements of inversive quaternion geometry were described by P.G. Gormley in his paper "Stereographic projection and the linear fractional group of transformations of quaternions". In 1968 Isaak Yaglom
Isaak Yaglom
Isaak Moiseevich Yaglom was a Soviet mathematician and author of popular mathematics books, some with his twin Akiva Yaglom.Yaglom received a Ph.D. from Moscow State University in 1945 as student of Veniamin Kagan. As the author of several books, translated into English, that have become academic...
's Complex Numbers in Geometry appeared in English, translated from Russian. There he uses P(D) to describe line geometry in the Euclidean plane and P(M) to describe it for Lobachevski's plane. Yaglom's text A Simple Non-Euclidean Geometry appeared in English in 1979. There in pages 174 to 200 he develops Minkowskian geometry and describes P(M) as the "inversive Minkowski plane". The Russian original of Yaglom's text was published in 1969. Between the two editions, Walter Benz
Walter Benz
Walter Benz is a German mathematician, an expert in geometry.Benz studied at the Johannes Gutenberg University of Mainz and received his doctoral degree in 1954, with Robert Furch as his advisor....
(1973) published his book which included the homogeneous coordinates taken from M.