Dual number
Encyclopedia
In linear algebra
, the dual numbers extend the real number
s by adjoining one new element ε with the property ε2 = 0 (ε is nilpotent
). The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra
over the real numbers. Every dual number has the form z = a + bε with a and b uniquely determined real numbers. The plane of all dual numbers is an "alternative complex plane" that complements the ordinary complex number
plane C and the plane of split-complex number
s.
, dual numbers can be represented as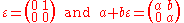
.
The sum and product of dual numbers are then calculated with ordinary matrix addition
and matrix multiplication
; both operations are commutative and associative.
This procedure is analogous to matrix representation of complex numbers.
Furthermore, the concept of the dual number is necessary when reading a matrix.
,
so the exponential function applied to the ε-axis covers only half the "circle".
If a ≠ 0 and m = b /a , then z = a(1 + m ε) is the polar decomposition of the dual number z, and the slope
m is its angular part.
The concept of a rotation in the dual number plane is equivalent to a vertical shear mapping since (1 + p ε)(1 + q ε) = 1 + (p+q) ε.
The dual number plane is used to represent the naive spacetime of Galileo in a study called Galilean invariance
since the classical event transformation with velocity v looks like: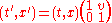
, that is 
.
in the real part of z, a cycle is a parabola
. In the Inversive ring geometry
of dual numbers one encounters "cyclic rotation" as a projectivity on the projective line over dual numbers. According to Yaglom (pp. 92,3), the cycle Z = {z : y = α x2} is invariant under the composition of the shear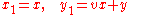
with the translation
.
This composition is a cyclic rotation; the concept has been further developed by V. V. Kisil.
terms, the dual numbers can be described as the quotient
of the polynomial ring
R[X] by the ideal
generated by the polynomial
X2,
The image of X in the quotient is the "imaginary" unit ε. With this description, it is clear that the dual numbers form a commutative ring
with characteristic
0. Moreover the inherited multiplication gives the dual numbers the structure of a commutative and associative algebra
over the reals of dimension two. The algebra is not a division algebra
or field
since the imaginary elements are not invertible. In fact, all of the nonzero imaginary elements are zero divisor
s (also see the section "Division"). The algebra of dual numbers is isomorphic to the exterior algebra
of
.
R one can define the dual numbers over R as the quotient
of the polynomial ring
R[X] by the ideal
(X2): the image of X then has square equal to zero and corresponds to the element ε from above.
This ring and its generalisations play an important part in the algebraic theory of derivations
and Kähler differential
s (purely algebraic differential form
s).
Over any ring R, the dual number a + bε is a unit
(i.e. multiplicatively invertible) if and only if a is a unit in R. In this case, the inverse of a + bε is a−1 − ba−2ε. As a consequence, we see that the dual numbers over any field
(or any commutative local ring
) form a local ring, its maximal ideal being the principal ideal
generated by ε.
. Consider the real dual numbers above. Given any real polynomial P(x) = p0+p1x+p2x2+...+pnxn, it is straightforward to extend the domain of this polynomial from the reals to the dual numbers. Then we have this result:
where 
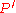is the derivative of 
.
By computing over the dual numbers, rather than over the reals, we can use this to compute derivatives of polynomials. More generally we may define division of dual numbers and then go on to define transcendental functions of dual numbers by defining f(a+bε) =
f(a)+bf ′(a)ε. By computing compositions of these functions over the dual numbers and examining the coefficient of ε in the result we find we have automatically computed the derivative of the composition.
This effect can be explained from the non-standard analysis
viewpoint. The imaginary unit ε of dual numbers is a close relative to infinitesimal
used in non-standard calculus
: indeed the square (or any higher power) of ε is exactly zero and the square of an infinitesimal is almost zero at this infinitesimal's scale (is an infinitesimal of a higher order more precisely).
, where they constitute one of the simplest non-trivial examples of a superspace
. The direction along ε is termed the "fermionic" direction, and the real component is termed the "bosonic" direction. The fermionic direction earns this name from the fact that fermion
s obey the Pauli exclusion principle
: under the exchange of coordinates, the quantum mechanical wave function changes sign, and thus vanishes if two coordinates are brought together; this physical idea is captured by the algebraic relation ε2 = 0.
in that the denominator is multiplied by its conjugate in order to cancel the non-real parts.
Therefore, to divide an equation of the form: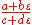
We multiply the top and bottom by the conjugate of the denominator: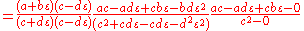
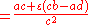
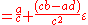
Which is defined when c is non-zero
.
If, on the other hand, c is zero while d is not, then the equation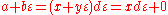
This means that the non-real part of the "quotient" is arbitrary and division is therefore not defined for purely nonreal dual numbers. Indeed, they are (trivially) zero divisors and clearly form an ideal
of the associative algebra
(and thus ring
) of the dual numbers.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the dual numbers extend the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s by adjoining one new element ε with the property ε2 = 0 (ε is nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
). The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the real numbers. Every dual number has the form z = a + bε with a and b uniquely determined real numbers. The plane of all dual numbers is an "alternative complex plane" that complements the ordinary complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane C and the plane of split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s.
Linear representation
Using matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, dual numbers can be represented as
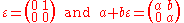.The sum and product of dual numbers are then calculated with ordinary matrix addition
Matrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
; both operations are commutative and associative.
This procedure is analogous to matrix representation of complex numbers.
Furthermore, the concept of the dual number is necessary when reading a matrix.
Geometry
The "unit circle" of dual numbers consists of those with a = 1 or −1 since these satisfy z z * = 1 where z * = a − bε. However, note that,so the exponential function applied to the ε-axis covers only half the "circle".
If a ≠ 0 and m = b /a , then z = a(1 + m ε) is the polar decomposition of the dual number z, and the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
m is its angular part.
The concept of a rotation in the dual number plane is equivalent to a vertical shear mapping since (1 + p ε)(1 + q ε) = 1 + (p+q) ε.
The dual number plane is used to represent the naive spacetime of Galileo in a study called Galilean invariance
Galilean invariance
Galilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
since the classical event transformation with velocity v looks like:
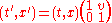, that is .Cycles
Given two dual numbers p, and q, they determine the set of z such that the Galilean angle between the lines from z to p and q is constant. This set is a cycle in the dual number plane; since the equation setting the difference in slopes of the lines to a constant is a quadratic equationQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
in the real part of z, a cycle is a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. In the Inversive ring geometry
Inversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
of dual numbers one encounters "cyclic rotation" as a projectivity on the projective line over dual numbers. According to Yaglom (pp. 92,3), the cycle Z = {z : y = α x2} is invariant under the composition of the shear
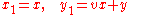with the translationTranslation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
.This composition is a cyclic rotation; the concept has been further developed by V. V. Kisil.
Algebraic properties
In abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
terms, the dual numbers can be described as the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[X] by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
X2,
- R[X]/<X2>.
The image of X in the quotient is the "imaginary" unit ε. With this description, it is clear that the dual numbers form a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0. Moreover the inherited multiplication gives the dual numbers the structure of a commutative and associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the reals of dimension two. The algebra is not a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
or field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
since the imaginary elements are not invertible. In fact, all of the nonzero imaginary elements are zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s (also see the section "Division"). The algebra of dual numbers is isomorphic to the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of
.Generalization
This construction can be carried out more generally: for a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R one can define the dual numbers over R as the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[X] by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
(X2): the image of X then has square equal to zero and corresponds to the element ε from above.
This ring and its generalisations play an important part in the algebraic theory of derivations
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
and Kähler differential
Kähler differential
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
s (purely algebraic differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s).
Over any ring R, the dual number a + bε is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
(i.e. multiplicatively invertible) if and only if a is a unit in R. In this case, the inverse of a + bε is a−1 − ba−2ε. As a consequence, we see that the dual numbers over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(or any commutative local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
) form a local ring, its maximal ideal being the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
generated by ε.
Differentiation
One application of dual numbers is automatic differentiationAutomatic differentiation
In mathematics and computer algebra, automatic differentiation , sometimes alternatively called algorithmic differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program...
. Consider the real dual numbers above. Given any real polynomial P(x) = p0+p1x+p2x2+...+pnxn, it is straightforward to extend the domain of this polynomial from the reals to the dual numbers. Then we have this result:
where 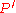is the derivative of .By computing over the dual numbers, rather than over the reals, we can use this to compute derivatives of polynomials. More generally we may define division of dual numbers and then go on to define transcendental functions of dual numbers by defining f(a+bε) =
f(a)+bf ′(a)ε. By computing compositions of these functions over the dual numbers and examining the coefficient of ε in the result we find we have automatically computed the derivative of the composition.
This effect can be explained from the non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
viewpoint. The imaginary unit ε of dual numbers is a close relative to infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
used in non-standard calculus
Non-standard calculus
In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
: indeed the square (or any higher power) of ε is exactly zero and the square of an infinitesimal is almost zero at this infinitesimal's scale (is an infinitesimal of a higher order more precisely).
Superspace
Dual numbers find applications in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, where they constitute one of the simplest non-trivial examples of a superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
. The direction along ε is termed the "fermionic" direction, and the real component is termed the "bosonic" direction. The fermionic direction earns this name from the fact that fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s obey the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
: under the exchange of coordinates, the quantum mechanical wave function changes sign, and thus vanishes if two coordinates are brought together; this physical idea is captured by the algebraic relation ε2 = 0.
Division
Division of dual numbers is defined when the real part of the denominator is non-zero. The division process is analogous to complex divisionComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
in that the denominator is multiplied by its conjugate in order to cancel the non-real parts.
Therefore, to divide an equation of the form:
We multiply the top and bottom by the conjugate of the denominator:
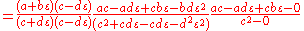
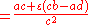
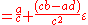
Which is defined when c is non-zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
.
If, on the other hand, c is zero while d is not, then the equation
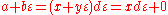
- has no solution if a is nonzero
- is otherwise solved by any dual number of the form
.
This means that the non-real part of the "quotient" is arbitrary and division is therefore not defined for purely nonreal dual numbers. Indeed, they are (trivially) zero divisors and clearly form an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of the associative algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
(and thus ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
) of the dual numbers.
See also
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Dual quaternionDual quaternionThe set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
- Exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
- Perturbation theoryPerturbation theoryPerturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...