Knots and graphs
Encyclopedia
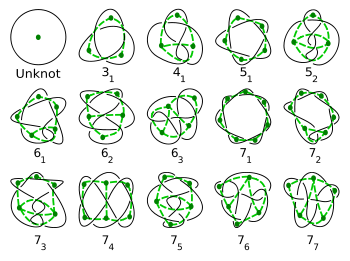
Knots
and graph theory
are related in some simple ways.
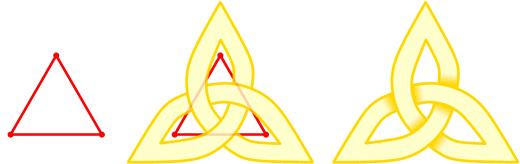
A knot in R3
(respectively in the 3-sphere
, S3), can be projected onto a plane R2 (resp. a sphere
S2).
This projection is generically regular, meaning that it is injective everywhere, except at a finite number of crossing points, which are the projections of only two points of the knot. Moreover, we require that the two directions at these points are not collinear
, that is to say the two threads project to two different directions of the plane (resp. the sphere) at the crossing point. In this condition, choosing a projection side, one can completely encode the isotopy class of the knot by its regular projection by recording a simple over/under information at these crossings.
In graph theory terms, a regular projection of a knot, or knot diagram is thus a 4-valent planar graph with over/under decorated vertices.
The Reidemeister move
s are local modifications of this decorated planar graph which allow to go from one diagram to any other diagram of the same knot (up to ambient isotopy of the plane).
, of dimension 2.
There is a way to attach a color, black or white, to all of these zones of dimension 2 in the following way: Choose the black color for the infinite zone, and at each crossing in turn, color the opposite zone in black. Proceed until every crossings have been taken into account. The Jordan curve theorem
implies that this procedure is well defined. It is called the medial graph of the 4-valent original graph.
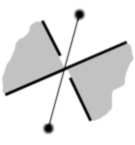
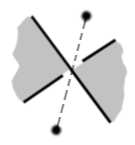Then you define a planar graph whose vertices are the white zones and whose edges are associated with every crossing. The over/under patterns associated to the crossings are now decorating the edges with a simple sign +/- or left/right according to the local configuration: viewing an edge from any of its two incident vertices, one of the two threads, whether left or right, goes above and the other one goes below. A left edge can be encoded as a plain edge, a right edge as a dashed edge. Changing the chirality of all edges amounts to reflecting the knot in a mirror.
We have thus constructed, for each knot diagram, a planar graph with "signed" edges associated to every crossing; the type of crossing that takes place at the middle of each edge is determined by the left/right sign of that edge.
s can be translated in this language: two edge-signed planar graphs are associated with the same knot if and only if you can go from one to the next by a series of Reidemeister moves.
s and knotless embeddings. A linkless embedding is an embedding of the graph with the property that any two cycles are unlink
ed; a knotless embedding is an embedding of the graph with the property that any single cycle is unknot
ted. The graphs that have linkless embeddings have a forbidden graph characterization involving the Petersen family
, a set of seven graphs that are intrinsically linked: no matter how they are embedded, some two cycles will be linked with each other. A full characterization of the graphs with knotless embeddings is not known, but the complete graph
K7 is one of the minimal forbidden graphs for knotless embedding: no matter how K7 is embedded, it will contain a cycle that forms a trefoil knot
.
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
are related in some simple ways.
Knot diagram
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(respectively in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, S3), can be projected onto a plane R2 (resp. a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
S2).
This projection is generically regular, meaning that it is injective everywhere, except at a finite number of crossing points, which are the projections of only two points of the knot. Moreover, we require that the two directions at these points are not collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, that is to say the two threads project to two different directions of the plane (resp. the sphere) at the crossing point. In this condition, choosing a projection side, one can completely encode the isotopy class of the knot by its regular projection by recording a simple over/under information at these crossings.
In graph theory terms, a regular projection of a knot, or knot diagram is thus a 4-valent planar graph with over/under decorated vertices.
The Reidemeister move
Reidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s are local modifications of this decorated planar graph which allow to go from one diagram to any other diagram of the same knot (up to ambient isotopy of the plane).
Medial graph
Another interpretation of a knot diagram as a decorated planar graph is more easy to deal with: The projection decomposes the plane in connected components, the graph itself of dimension 1, and an infinite zone and components which are homeomorphic to disksDisk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
, of dimension 2.
There is a way to attach a color, black or white, to all of these zones of dimension 2 in the following way: Choose the black color for the infinite zone, and at each crossing in turn, color the opposite zone in black. Proceed until every crossings have been taken into account. The Jordan curve theorem
Jordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
implies that this procedure is well defined. It is called the medial graph of the 4-valent original graph.
We have thus constructed, for each knot diagram, a planar graph with "signed" edges associated to every crossing; the type of crossing that takes place at the middle of each edge is determined by the left/right sign of that edge.
Reidemeister moves
The Reidemeister moveReidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s can be translated in this language: two edge-signed planar graphs are associated with the same knot if and only if you can go from one to the next by a series of Reidemeister moves.
Linkless and knotless embedding
In two dimensions, only the planar graphs may be embedded into the Euclidean plane without crossings, but in three dimensions, any undirected graph may be embedded into space without crossings. However, a spatial analogue of the planar graphs is provided by the graphs with linkless embeddingLinkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
s and knotless embeddings. A linkless embedding is an embedding of the graph with the property that any two cycles are unlink
Unlink
In the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...
ed; a knotless embedding is an embedding of the graph with the property that any single cycle is unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
ted. The graphs that have linkless embeddings have a forbidden graph characterization involving the Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
, a set of seven graphs that are intrinsically linked: no matter how they are embedded, some two cycles will be linked with each other. A full characterization of the graphs with knotless embeddings is not known, but the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K7 is one of the minimal forbidden graphs for knotless embedding: no matter how K7 is embedded, it will contain a cycle that forms a trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
.