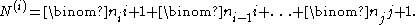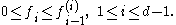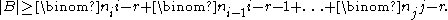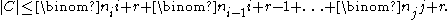In algebraic combinatorics

Algebraic combinatorics

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....

, the Kruskal–Katona theorem gives a complete characterization of the f-vectors of abstract simplicial complex

Abstract simplicial complex

In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...

es. It includes as a special case the Erdős–Ko–Rado theorem

Erdos–Ko–Rado theorem

In combinatorics, the Erdős–Ko–Rado theorem of Paul Erdős, Chao Ko, and Richard Rado is a theorem on hypergraphs, specifically, on uniform hypergraphs of rank r.The theorem is as follows...

 and can be restated in terms of uniform hypergraphs

Hypergraph

In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...

. The theorem is named after Joseph Kruskal

Joseph Kruskal

Joseph Bernard Kruskal, Jr. was an American mathematician, statistician, computer scientist and psychometrician. He was a student at the University of Chicago and at Princeton University, where he completed his Ph.D. in 1954, nominally under Albert W...

 and Gyula O. H. Katona

Gyula O. H. Katona

Gyula O. H. Katona is a Hungarian mathematician known for his work in combinatorial set theory, and especially for the Kruskal–Katona theorem and his elegant proof of the Erdős–Ko–Rado theorem...

. It was independently proved by Marcel Schützenberger, but his contribution escaped notice for several years.

Statement

Given two positive integers N and i, there is a unique way to expand N as a sum of binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

s as follows:

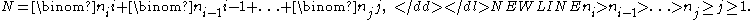
This expansion can be constructed by applying the greedy algorithm

Greedy algorithm

A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....

: set n_i to be the maximal n such that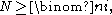 replace N with the difference, i with i − 1, and repeat until the difference becomes zero. Define

Statement for simplicial complexes

An integral vector (f₀, f₁, … f_d −1 ) is the f-vector of some (d −1 )-dimensional simplicial complex if and only if

Statement for uniform hypergraphs

Let A be a set consisting of N distinct i-element subsets of a fixed set U ("the universe") and B be the set of all (i −r )-element subsets of the sets in A. Expand N as above. Then the cardinality of B is bounded below as follows:

Suppose that U is the union of the sets in A and that C is the set of all (i + r)-element supersets of the sets in A. Then the cardinality of C is bounded above as follows:

Ingredients of the proof

For every positive i, list all i-element subsets a₁ < a₂ < … a_i of the set N of natural numbers in the reverse lexicographic order. For example, for i = 3, the list begins

Given a vector f = (f₀, f₁, …, f_d −1 ) with positive integer components, let Δ_f be the subset of the power set 2^N consisting of the empty set together with the first f_i − 1 i-element subsets of N in the list for i = 1, …, d. Then the following conditions are equivalent:

1. Vector f is the f-vector of a simplicial complex Δ.
2. Δ_f is a simplicial complex.
3. 

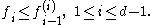
The difficult implication is 1 ⇒ 2.

External links

• Kruskal-Katona theorem on the polymath1 wiki

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.