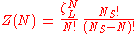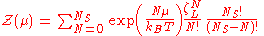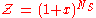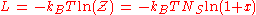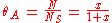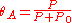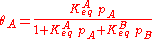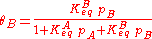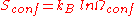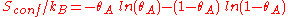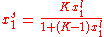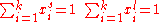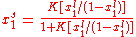The Langmuir adsorption model is the most common model used to quantify the amount of adsorbate adsorbed

Adsorption

Adsorption is the adhesion of atoms, ions, biomolecules or molecules of gas, liquid, or dissolved solids to a surface. This process creates a film of the adsorbate on the surface of the adsorbent. It differs from absorption, in which a fluid permeates or is dissolved by a liquid or solid...

 on an adsorbent as a function of partial pressure

Partial pressure

In a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture....

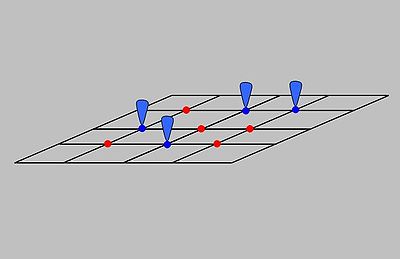
 or concentration at a given temperature. It considers adsorption of an ideal gas onto an idealized surface. The gas is presumed to bind at a series of distinct sites on the surface of the solid as indicated in Figure 1, and the adsorption process was treated as a reaction where a gas molecule 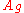reacts with an empty site, S, to yield an adsorbed complex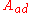

Basic assumptions of the model

Inherent within this model, the following assumptions
are valid specifically for the simplest case: the adsorption of a single adsorbate onto a series of equivalent sites on the surface of the solid.

1. The surface containing the adsorbing sites is perfectly flat plane with no corrugations (assume the surface is homogeneous) .
2. The adsorbing gas adsorbs into an immobile state.
3. All sites are equivalent.
4. Each site can hold at most one molecule of A (mono-layer coverage only).
5. There are no interactions between adsorbate molecules on adjacent sites.

Kinetic Derivation

This section

provides a kinetic derivation for a single adsorbate case. The multiple adsorbate case is covered in the Competitive adsorption sub-section.
The model assumes adsorption and desorption

Desorption

Desorption is a phenomenon whereby a substance is released from or through a surface. The process is the opposite of sorption . This occurs in a system being in the state of sorption equilibrium between bulk phase and an adsorbing surface...

 as being elementary processes, where the rate of adsorption r_ad and the rate of desorption r_d are given by:



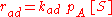
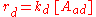
where P_A is the partial pressure of A over the surface, [S] is the concentration of bare sites in number/m², [A_ad] is the surface concentration of A in molecules/m², and k_ad and k_d are constants.

At equilibrium, the rate of adsorption equals the rate of desorption. Setting r_ad=r_d and rearranging, we obtain:


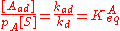
The concentration of all sites [S₀] is the sum of the concentration of free sites [S] and of occupied sites:


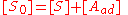
Combining this with the equilibrium equation, we get:


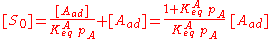
We define now the fraction of the surface sites covered with A, θ_A, as:


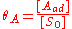
This, applied to the previous equation that combined site balance and equilibriem, yields the Langmuir adsorption isotherm:

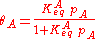
Statistical Mechanical Derivation

This derivation

was originally provided by Volmer and Mahnert in 1925.

The partition function

Partition function (statistical mechanics)

Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...

 of the finite number of adsorbents adsorbed on a surface, in a canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

 is given by

where is the partition function of a single adsorbed molecule, 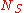are the number of sites available for adsorption. Hence, N, which is the number of molecules that can be adsorbed, can be less or equal to N_s. The first term of Z(n) accounts the total partition function of the different molecules by taking a product of the individual partition functions (Refer to Partition function of subsystems). The latter term accounts for the overcounting arising due to the indistinguishable nature of the adsorption sites. The grand canonical partition function is given by

As it has the form of binomial series

Binomial theorem

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...

, the summation is reduced to

where

The Landau free energy, which is generalized Helmholtz free energy

Helmholtz free energy

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...

 is given by

According to the Maxwell relations

Maxwell relations

Maxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...

 regarding the change of the Helmholtz free energy with respect to the chemical potential,


which gives

Now, invoking the condition that the system is in equilibrium, the chemical potential of the adsorbates is equal to that of the gas surroundings the absorbent.

where N^3D is the number of gas molecules, Z^3D is the partition function of the gas molecules and A_g=-k_BT ln Z_g. Further, we get

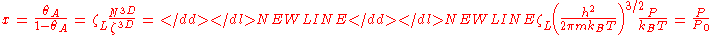
where



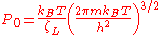
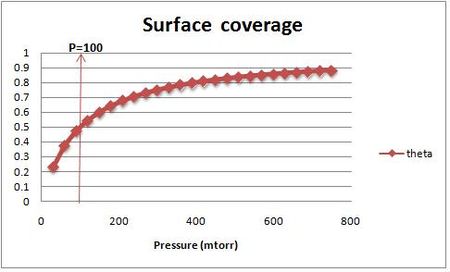
Finally , we have

It is plotted in the figure alongside demonstrating the surface coverage increases quite rapidly with the partial pressure of the adsorbants but levels off after P reaches P₀.

Competitive Adsorption

The previous derivations assumes that there is only one species, A, adsorbing onto the surface. This section considers the case when there are two distinct adsorbates present in the system.Consider two species A and B that compete for the same adsorption sites. The following assumptions are applied here:

1. All the sites are equivalent.
2. Each site can hold at most one molecule of A or one molecule of B, but not both.
3. There are no interactions between adsorbate molecules on adjacent sites.

As derived using kinetical considerations, the equilibrium constants for both A and B are given by


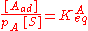
and


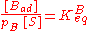
The site balance states that the concentration of total sites [S₀] is equal to the sum of free sites, sites occupied by A and sites occupied by B:


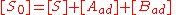
Inserting the equilibrium equations and rearranging in the same way we did for the single-species adsorption, we get similar expressions for both θ_A and θ_B:

Dissociative Adsorption

The other case of special importance is when a molecule D₂ dissociates into two atoms upon adsorption. Here, the following assumptions would be held to be valid:

1. D₂ completely dissociates to two molecules of D upon adsorption.
2. The D atoms adsorb onto distinct sites on the surface of the solid and then move around and equilibrate.
3. All sites are equivalent.
4. Each site can hold at most one atom of D.
5. There are no interactions between adsorbate molecules on adjacent sites.

Using similar kinetic considerations, we get:


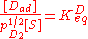
The 1/2 exponent on p_D2 arises because one gas phase molecule produces two adsorbed species. Applying the site balance as done above:

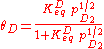
Entropic considerations

One of the thermodynamic motivation of molecules adsorbing on the surface is the fact that it leads drastic decrease in the entropy of the molecule as it becomes bound to the surfaces sites on the surface. To find the entropy decrease, we find the entropy of the molecule when in the adsorbed condition.

Using Stirling's approximation

Stirling's approximation

In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...

, we have,

On the other hand, the entropy of a molecule of an ideal gas is



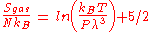
where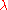 is the Thermal de Broglie wavelength of the gas molecule.

Disadvantages of the model

The Langmuir adsorption model deviates significantly in many cases, primarily because it fails to account for the surface roughness of the adsorbate. Rough inhomogeneous surfaces have multiple site-types available for adsorption, and some parameters vary from site to site, such as the heat of adsorption.

The model also ignores adsorbate/adsorbate interactions. Experimentally, there is clear evidence for adsorbate/adsorbate interactions in heat of adsorption data. There are two kinds of adsorbate/adsorbate interactions: direct interaction and indirect interaction. Direct interactions are between adjacent adsorbed molecules, which could make adsorbing near another adsorbate molecule more or less favorable and greatly affects high-coverage behavior. In indirect interactions, the adsorbate changes the surface around the adsorbed site, which in turn affects the adsorption of other adsorbate molecules nearby.

Modifications of the Langmuir Adsorption Model

The modifications try to account for the points mentioned in above section like surface roughness, inhomogeneity, and adsorbate-adsorbate interactions.

The Freundlich Adsorption Isotherm

The Freundlich isotherm is the most important multisite adsorption isotherm for rough surfaces.


where α_F and C_F are fitting parameters. This equation implies that if one makes a log-log plot of adsorption data, the data will fit a straight line. The Freundlich isotherm has two parameters while Langmuir's equations has only one: as a result, it often fits the data on rough surfaces better than the Langmuir's equations.

A related equation is the Toth equation. Rearranging the Langmuir equation, one can obtain:


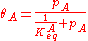
Toth modified this equation by adding two parameters, α_T0 and C_T0 as follows:

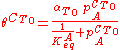
The Temkin Adsorption Isotherm

This isotherm takes into accounts of indirect adsorbate-adsorbate interactions on adsorption isotherms. Temkin noted experimentally that heats of adsorption would more often decrease than increase with increasing coverage.

The heat of adsorption ΔH_ad is defined as:


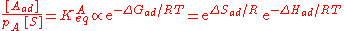
He derived a model assuming that as the surface is loaded up with adsorbate, the heat of adsorption of all the molecules in the layer would decrease linearly with coverage due to adsorbate/adsorbate interactions:


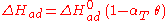
where α_T is a fitting parameter. Assuming the Langmuir Adsorption isotherm still applied to the adsorbed layer, is expected to vary with coverage, as follows:


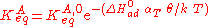
Langmuir's isotherm can be rearranged to this form:


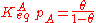
Substituting the expression of the equilibrium constant and taking the natural logarithm:

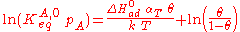
BET equation

In a groundbreaking paper, Brunauer, Emmett and Teller derived the first isotherm for multilayer adsorption. It assumes a random distribution of sites that are empty or that are covered with by one monolayer, two layers and so on, as illustrated alongside. The main equation of this model is:


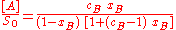
where



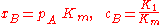
and [A] is the total concentration of molecules on the surface, given by:


where



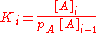
in which [A]₀ is the number of bare sites, and [A]_i is the number of surface sites covered by i molecules.

Adsorption of binary liquid adsorption on solids

This section describes the surface coverage when the adsorbate is in liquid phase and is a binary mixture

For ideal both phases - no lateral interactions, homogeneous surface - the composition of a surface phase for a binary liquid system in contact with solid surface is given by a classic Everett isotherm equation (being a simple analogue of Langmuir equation), where the components are interchangeable (i.e. "1" may be exchanged to "2") without change of eq. form:

where the normal definition of multicomponent system is valid as follows :

By simple rearrangement, we get

This equation describes competition of components "1" and "2".

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.