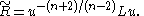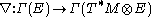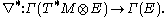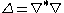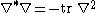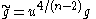Laplacian operators in differential geometry
Encyclopedia
In differential geometry there are a number of second-order, linear, elliptic
differential operators bearing the name Laplacian. This article provides an overview of some of them.
metric. When applied to functions (i.e, tensors of rank 0), the connection
Laplacian is often called the Laplace–Beltrami operator. It is defined as the trace of the second covariant derivative:
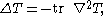
where T is any tensor,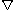
is the Levi-Civita connection
associated to the metric, and the trace is taken with respect to
the metric. Recall that the second covariant derivative of T is defined as
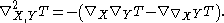
Note that with this definition, the connection Laplacian has negative spectrum. On functions, it agrees with
the operator given as the divergence of the gradient.
it is a second order operator on each exterior power of the cotangent bundle
.) This operator is defined on any manifold equipped with
a Riemannian- or pseudo-Riemannian
metric.
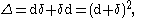
where d is the exterior derivative
or differential and δ is the codifferential. The Hodge Laplacian on a compact manifold has nonnegative spectrum.
The connection Laplacian may also be taken to act on differential forms by restricting it to act on skew-symmetric tensors. The connection Laplacian differs from the Hodge Laplacian by means of a Weitzenböck identity
.
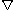. This connection gives rise to a differential operator
where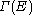
denotes smooth sections of E, and T*M is the cotangent bundle
of M. It is possible to take the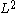
-adjoint of 
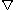, giving a differential operator
The Bochner Laplacian is given by
which is a second order operator acting on sections of the vector bundle E. Note that the connection Laplacian and Bochner Laplacian differ only by a sign:
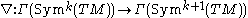to be the symmetrized covariant derivative. The Lichnerowicz Laplacian is then defined by 
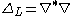, where 
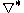is the formal adjoint. The Lichnerowicz Laplacian differs from the usual tensor Laplacian by a Weitzenbock formula involving the Riemann curvature tensor
, and has natural applications in the study of Ricci flow
and the prescribed Ricci curvature problem
.
, one can define the conformal Laplacian as an operator on smooth functions; it differs from the Laplace–Beltrami operator by a term involving the scalar curvature
of the underlying metric. In dimension n ≥ 3, the conformal Laplacian, denoted L, acts on a smooth function u by
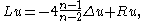
where Δ is the Laplace-Beltrami operator (of negative spectrum), and R is the scalar curvature. This operator often makes an appearance when studying how the scalar curvature behaves under a conformal change of a Riemannian metric. If n ≥ 3 and g is a metric and u is a smooth, positive function, then the conformal
metric
has scalar curvature given by
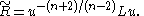
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
differential operators bearing the name Laplacian. This article provides an overview of some of them.
Connection Laplacian
The connection Laplacian is a differential operator acting on the various tensor bundles of a manifold, defined in terms of a Riemannian- or pseudo-RiemannianPseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
metric. When applied to functions (i.e, tensors of rank 0), the connection
Laplacian is often called the Laplace–Beltrami operator. It is defined as the trace of the second covariant derivative:
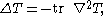
where T is any tensor,
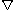is the Levi-Civita connectionLevi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
associated to the metric, and the trace is taken with respect to
the metric. Recall that the second covariant derivative of T is defined as
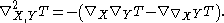
Note that with this definition, the connection Laplacian has negative spectrum. On functions, it agrees with
the operator given as the divergence of the gradient.
Hodge Laplacian
The Hodge Laplacian, also known as the Laplace–de Rham operator, is differential operator on acting on differential forms. (Abstractly,it is a second order operator on each exterior power of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.) This operator is defined on any manifold equipped with
a Riemannian- or pseudo-Riemannian
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
metric.
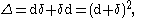
where d is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
or differential and δ is the codifferential. The Hodge Laplacian on a compact manifold has nonnegative spectrum.
The connection Laplacian may also be taken to act on differential forms by restricting it to act on skew-symmetric tensors. The connection Laplacian differs from the Hodge Laplacian by means of a Weitzenböck identity
Weitzenbock identity
In mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity expresses a relationship between two second-order elliptic operators on a manifold with the same leading symbol...
.
Bochner Laplacian
The Bochner Laplacian is defined differently from the connection Laplacian, but the two will turn out to differ only by a sign, whenever the former is defined. Let M be a compact, oriented manifold equipped with a metric. Let E be a vector bundle over M equipped a fiber metric and a compatible connection,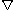. This connection gives rise to a differential operator
where
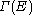denotes smooth sections of E, and T*M is the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of M. It is possible to take the
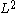-adjoint of 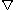, giving a differential operator
The Bochner Laplacian is given by
which is a second order operator acting on sections of the vector bundle E. Note that the connection Laplacian and Bochner Laplacian differ only by a sign:
Lichnerowicz Laplacian
The Lichnerowicz Laplacian is defined on symmetric tensors by taking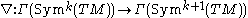 to be the symmetrized covariant derivative. The Lichnerowicz Laplacian is then defined by 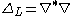, where 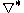is the formal adjoint. The Lichnerowicz Laplacian differs from the usual tensor Laplacian by a Weitzenbock formula involving the Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, and has natural applications in the study of Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
and the prescribed Ricci curvature problem
Prescribed Ricci curvature problem
In Riemannian geometry, a branch of mathematics, the prescribed Ricci curvature problem is as follows: given a smooth manifold M and a symmetric 2-tensor h, construct a metric on M whose Ricci curvature tensor equals h.-References:...
.
Conformal Laplacian
On a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, one can define the conformal Laplacian as an operator on smooth functions; it differs from the Laplace–Beltrami operator by a term involving the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
of the underlying metric. In dimension n ≥ 3, the conformal Laplacian, denoted L, acts on a smooth function u by
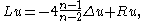
where Δ is the Laplace-Beltrami operator (of negative spectrum), and R is the scalar curvature. This operator often makes an appearance when studying how the scalar curvature behaves under a conformal change of a Riemannian metric. If n ≥ 3 and g is a metric and u is a smooth, positive function, then the conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
metric
has scalar curvature given by