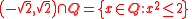Least-upper-bound property
Encyclopedia
In mathematics
, the least-upper-bound property is a fundamental property of the real number
s and certain other ordered sets. The property states that any non-empty set of real numbers that has an upper bound
necessarily has a least upper bound (or supremum).
The least-upper-bound property is one form of the completeness axiom
for the real numbers, and is sometimes referred to as Dedekind completeness. It can be used to prove many of the fundamental results of real analysis
, such as the intermediate value theorem
, the Bolzano–Weierstrass theorem
, the extreme value theorem
, and the Heine–Borel theorem
. It is usually taken as an axiom in synthetic constructions of the real numbers (see least upper bound axiom
), and it is also intimately related to the construction of the real numbers using Dedekind cut
s.
In order theory
, this property can be generalized to a notion of completeness
for any partially ordered set
. A linearly ordered set that is dense
and has the least upper bound property is called a linear continuum
.
s.
The least-upper-bound property states that any non-empty set of real numbers that has an upper bound must have a least upper bound.
of a partially ordered set
, with “real number” replaced by “element of ”. In this case, we say that has the least-upper-bound property if every subset of with an upper bound has a least upper bound.
For example, the set of rational number
s does not have the least-upper-bound property under the usual order. For instance, the set
has an upper bound in , but does not have a least upper bound in (since the square root of two is irrational
). The construction of the real numbers using Dedekind cut
s takes advantage of this failure by defining the irrational numbers as the least upper bounds of certain subsets of the rationals.
, such as the convergence of Cauchy sequence
s or the nested intervals theorem. The logical status of the property depends on the construction of the real numbers used: in the synthetic approach, the property is usually taken as an axiom for the real numbers (see least upper bound axiom
); in a constructive approach, the property must be proved as a theorem
, either directly from the construction or as a consequence of some other form of completeness.
Then and as . It follows that both sequences are Cauchy and have the same limit , which must be the least upper bound for .
.
, and suppose that and . In this case, the intermediate value theorem
states that must have a root in the interval . This theorem can proved by considering the set
That is, is the initial segment of that takes negative values under . Then is an upper bound for , and the least upper bound must be a root of .
for states that every sequence
of real numbers in a closed interval must have a convergent subsequence
. This theorem can be proved by considering the set
Clearly is an upper bound for , so has a least upper bound . Then must be a limit point
of the sequence , and it follows that has a subsequence that converges to .
and let , where if has no upper bound. The extreme value theorem
states that is finite and for some . This can be proved by considering the set
If is the least upper bound of this set, then it follows from continuity that .
s that covers
. Then the Heine–Borel theorem
states that some finite subcollection of covers as well. This statement can be proved by considering the set
This set must have a least upper bound . But is itself an element of some open set , and it follows that can be covered by finitely many for some sufficiently small . This proves that , and it also yields a contradiction unless .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the least-upper-bound property is a fundamental property of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and certain other ordered sets. The property states that any non-empty set of real numbers that has an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
necessarily has a least upper bound (or supremum).
The least-upper-bound property is one form of the completeness axiom
Completeness axiom
In mathematics the completeness axiom, also called Dedekind completeness of the real numbers, is a fundamental property of the set R of real numbers...
for the real numbers, and is sometimes referred to as Dedekind completeness. It can be used to prove many of the fundamental results of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, such as the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
, the Bolzano–Weierstrass theorem
Bolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
, the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
, and the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
. It is usually taken as an axiom in synthetic constructions of the real numbers (see least upper bound axiom
Least upper bound axiom
The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom of real analysis stating that the set R of real numbers has the least-upper-bound property. That is, if a nonempty set of real numbers has an upper bound, then it has a least upper bound...
), and it is also intimately related to the construction of the real numbers using Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s.
In order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, this property can be generalized to a notion of completeness
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
for any partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
. A linearly ordered set that is dense
Dense order
In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x...
and has the least upper bound property is called a linear continuum
Linear continuum
In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two members there is another, and which "lacks gaps" in the...
.
Statement for real numbers
Let be a non-empty set of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
- A real number is called an upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for if for all . - A real number is the least upper bound (or supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
) for if is an upper bound for and for every upper bound of .
The least-upper-bound property states that any non-empty set of real numbers that has an upper bound must have a least upper bound.
Generalization to ordered sets
More generally, one may define upper bound and least upper bound for any subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
, with “real number” replaced by “element of ”. In this case, we say that has the least-upper-bound property if every subset of with an upper bound has a least upper bound.
For example, the set of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s does not have the least-upper-bound property under the usual order. For instance, the set
has an upper bound in , but does not have a least upper bound in (since the square root of two is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
). The construction of the real numbers using Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s takes advantage of this failure by defining the irrational numbers as the least upper bounds of certain subsets of the rationals.
Logical status
The least-upper-bound property is equivalent to other forms of the completeness axiomCompleteness axiom
In mathematics the completeness axiom, also called Dedekind completeness of the real numbers, is a fundamental property of the set R of real numbers...
, such as the convergence of Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s or the nested intervals theorem. The logical status of the property depends on the construction of the real numbers used: in the synthetic approach, the property is usually taken as an axiom for the real numbers (see least upper bound axiom
Least upper bound axiom
The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom of real analysis stating that the set R of real numbers has the least-upper-bound property. That is, if a nonempty set of real numbers has an upper bound, then it has a least upper bound...
); in a constructive approach, the property must be proved as a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, either directly from the construction or as a consequence of some other form of completeness.
Proof using Cauchy sequences
It is possible to prove the least-upper-bound property using the assumption that every Cauchy sequence of real numbers converges. Let be a nonempty set of real numbers, and suppose that has an upper bound . Since is nonempty, there exists a real number that is not an upper bound for . Define sequences and recursively as follows:- Check whether is an upper bound for .
- If it is, let and let .
- Otherwise there must be an element in so that . Let and let .
Then and as . It follows that both sequences are Cauchy and have the same limit , which must be the least upper bound for .
Applications
The least-upper-bound property of can be used to prove many of the main foundational theorems in real analysisReal analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
.
Intermediate value theorem
Let be a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and suppose that and . In this case, the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
states that must have a root in the interval . This theorem can proved by considering the set
- .
That is, is the initial segment of that takes negative values under . Then is an upper bound for , and the least upper bound must be a root of .
Bolzano–Weierstrass theorem
The Bolzano–Weierstrass theoremBolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
for states that every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of real numbers in a closed interval must have a convergent subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
. This theorem can be proved by considering the set
- .
Clearly is an upper bound for , so has a least upper bound . Then must be a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of the sequence , and it follows that has a subsequence that converges to .
Extreme value theorem
Let be a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and let , where if has no upper bound. The extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
states that is finite and for some . This can be proved by considering the set
- .
If is the least upper bound of this set, then it follows from continuity that .
Heine–Borel theorem
Let be a closed interval in , and let be a collection of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s that covers
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
. Then the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
states that some finite subcollection of covers as well. This statement can be proved by considering the set
- .
This set must have a least upper bound . But is itself an element of some open set , and it follows that can be covered by finitely many for some sufficiently small . This proves that , and it also yields a contradiction unless .