
Lebesgue-Stieltjes integration
Encyclopedia
In measure-theoretic analysis
and related branches of mathematics
, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration
, preserving the many advantages of the former in a more general measure-theoretic framework. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation
on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and conversely every regular Borel measure on the real line is of this kind.
Lebesgue–Stieltjes integral
s, named for Henri Leon Lebesgue and Thomas Joannes Stieltjes
, are also known as Lebesgue–Radon integrals or just Radon integrals, after Johann Radon
, to whom much of the theory is due. They find common application in probability
and stochastic process
es, and in certain branches of analysis
including potential theory
.
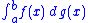
is defined when ƒ : [a,b] → R is Borel-measurable
and bounded
and g : [a,b] → R is of bounded variation
in [a,b] and right-continuous, or when ƒ is non-negative and g is monotone and right-continuous. To start, assume that ƒ is non-negative and g is monotone non-decreasing and right-continuous. Define w((s,t]) := g(t) − g(s) and w({a}) := 0 (Alternatively, the construction works for g left-continuous, w([s,t)) := g(t) − g(s) and w({b}) := 0).
By Carathéodory's extension theorem
, there is a unique Borel measure μg on
[a,b] which agrees with w on every interval I. The measure μg arises from an outer measure
(in fact, a metric outer measure
) given by
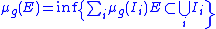
the infimum
taken over all coverings of E by countably many semiopen intervals. This measure is sometimes called the Lebesgue–Stieltjes measure associated with g.
The Lebesgue–Stieltjes integral
is defined as the Lebesgue integral of ƒ
with respect to the measure μg in the usual way. If g is non-increasing, then define
the latter integral being defined by the preceding construction.
If g is of bounded variation and ƒ is bounded, then it is possible to write
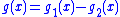
where is the total variation
of g in the interval [a,x], and g2(x) = g1(x) − g(x).
Both g1 and g2 are monotone non-decreasing. Now the Lebesgue–Stieltjes integral with respect to g is defined by
where the latter two integrals
are well-defined by the preceding construction.
that extends the usual Riemann–Stieltjes integral. Let g be a non-increasing right-continuous function on [a,b], and define I(ƒ) to be the Riemann–Stieltjes integral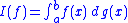
for all continuous functions ƒ. The functional I defines a Radon measure
on [a,b]. This functional can then be extended to the class of all non-negative functions by setting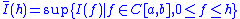
and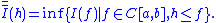
For Borel measurable functions, one has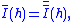
and either side of the identity then defines the Lebesgue–Stieltjes integral of h. The outer measure μg is defined via
where χA is the indicator function of A.
Integrators of bounded variation are handled as above by decomposing into positive and negative variations.
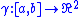 is a rectifiable curve in the plane
is a rectifiable curve in the plane
and is Borel measurable. Then we may define the length
is Borel measurable. Then we may define the length
of with respect to the Euclidean metric weighted by
with respect to the Euclidean metric weighted by 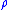 to
to
be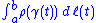 , where
, where  is the length
is the length
of the restriction of to
to 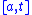 .
.
This is sometimes called the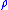 -length of
-length of  .
.
This notion is quite useful for
various applications: for example, in muddy terrain the speed in which a person can move may
depend on how deep the mud is. If denotes the inverse of the walking speed
denotes the inverse of the walking speed
at or near , then the
, then the 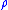 -length of
-length of  is the
is the
time it would take to traverse . The concept of extremal length
. The concept of extremal length
uses
this notion of the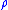 -length of curves and is useful in the study of
-length of curves and is useful in the study of
conformal mappings
.
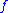 is said to be "regular" at a point
is said to be "regular" at a point  if the right and left hand limits
if the right and left hand limits 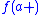 and
and  exist, and the function takes the average value,
exist, and the function takes the average value,
at the limiting point. Given two functions and
and  of finite variation, if at each point either
of finite variation, if at each point either  or
or  is continuous, or if both
is continuous, or if both  and
and  are regular, then there is an integration by parts
are regular, then there is an integration by parts
formula for the Lebesgue–Stieltjes integral:
where . Under a slight generalization of this formula, the extra conditions on
. Under a slight generalization of this formula, the extra conditions on  and
and  can be dropped.
can be dropped.
An alternative result, of significant importance in the theory of Stochastic calculus
is the following. Given two functions and
and  of finite variation, which are both right-continuous and have left-limits (they are cadlag
of finite variation, which are both right-continuous and have left-limits (they are cadlag
functions) then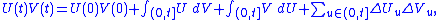
where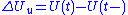 . This result can be seen as a precursor to Ito's lemma
. This result can be seen as a precursor to Ito's lemma
, and is of use in the general theory of Stochastic integration. The final term is , which arises from the quadratic covariation of
, which arises from the quadratic covariation of  and
and  . (The earlier result can then be seen as a result pertaining to the Stratonovich integral
. (The earlier result can then be seen as a result pertaining to the Stratonovich integral
.)
, and the Lebesgue–Stieltjes integral of f with respect to g is equivalent to the Lebesgue integral of f.
real-valued function of a real variable and v is a non-decreasing real function, the Lebesgue–Stieltjes integral is equivalent to the Riemann–Stieltjes integral, in which case we often write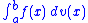
for the Lebesgue–Stieltjes integral, letting the measure μv remain implicit. This is particularly common in probability theory
when v is the cumulative distribution function
of a real-valued random variable X, in which case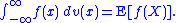
(See the article on Riemann–Stieltjes integration for more detail on dealing with such cases.)
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
, preserving the many advantages of the former in a more general measure-theoretic framework. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and conversely every regular Borel measure on the real line is of this kind.
Lebesgue–Stieltjes integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s, named for Henri Leon Lebesgue and Thomas Joannes Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
, are also known as Lebesgue–Radon integrals or just Radon integrals, after Johann Radon
Johann Radon
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
, to whom much of the theory is due. They find common application in probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, and in certain branches of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
including potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
Definition
The Lebesgue–Stieltjes integral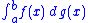
is defined when ƒ : [a,b] → R is Borel-measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
and bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
and g : [a,b] → R is of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
in [a,b] and right-continuous, or when ƒ is non-negative and g is monotone and right-continuous. To start, assume that ƒ is non-negative and g is monotone non-decreasing and right-continuous. Define w((s,t]) := g(t) − g(s) and w({a}) := 0 (Alternatively, the construction works for g left-continuous, w([s,t)) := g(t) − g(s) and w({b}) := 0).
By Carathéodory's extension theorem
Carathéodory's extension theorem
In measure theory, Carathéodory's extension theorem states that any σ-finite measure defined on a given ring R of subsets of a given set Ω can be uniquely extended to the σ-algebra generated by R...
, there is a unique Borel measure μg on
[a,b] which agrees with w on every interval I. The measure μg arises from an outer measure
Outer measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
(in fact, a metric outer measure
Metric outer measure
In mathematics, a metric outer measure is an outer measure μ defined on the subsets of a given metric space such that\mu = \mu + \mu for every pair of positively separated subsets A and B of X....
) given by
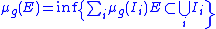
the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
taken over all coverings of E by countably many semiopen intervals. This measure is sometimes called the Lebesgue–Stieltjes measure associated with g.
The Lebesgue–Stieltjes integral

is defined as the Lebesgue integral of ƒ
with respect to the measure μg in the usual way. If g is non-increasing, then define

the latter integral being defined by the preceding construction.
If g is of bounded variation and ƒ is bounded, then it is possible to write
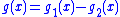
where is the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of g in the interval [a,x], and g2(x) = g1(x) − g(x).
Both g1 and g2 are monotone non-decreasing. Now the Lebesgue–Stieltjes integral with respect to g is defined by

where the latter two integrals
are well-defined by the preceding construction.
Daniell integral
An alternative approach is to define the Lebesgue–Stieltjes integral as the Daniell integralDaniell integral
In mathematics, the Daniell integral is a type of integration that generalizes the concept of more elementary versions such as the Riemann integral to which students are typically first introduced...
that extends the usual Riemann–Stieltjes integral. Let g be a non-increasing right-continuous function on [a,b], and define I(ƒ) to be the Riemann–Stieltjes integral
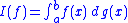
for all continuous functions ƒ. The functional I defines a Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
on [a,b]. This functional can then be extended to the class of all non-negative functions by setting
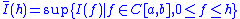
and
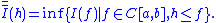
For Borel measurable functions, one has
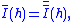
and either side of the identity then defines the Lebesgue–Stieltjes integral of h. The outer measure μg is defined via

where χA is the indicator function of A.
Integrators of bounded variation are handled as above by decomposing into positive and negative variations.
Example
Suppose that is a rectifiable curve in the plane
is a rectifiable curve in the planeand
 is Borel measurable. Then we may define the length
is Borel measurable. Then we may define the lengthof
 with respect to the Euclidean metric weighted by
with respect to the Euclidean metric weighted by 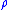 to
tobe
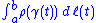 , where
, where  is the length
is the lengthof the restriction of
 to
to 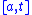 .
.This is sometimes called the
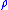 -length of
-length of  .
.This notion is quite useful for
various applications: for example, in muddy terrain the speed in which a person can move may
depend on how deep the mud is. If
 denotes the inverse of the walking speed
denotes the inverse of the walking speedat or near
 , then the
, then the 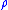 -length of
-length of  is the
is thetime it would take to traverse
 . The concept of extremal length
. The concept of extremal lengthExtremal length
In the mathematical theory of conformal and quasiconformal mappings, the extremal length of a collection of curves \Gamma is a conformal invariant of \Gamma. More specifically, suppose thatD is an open set in the complex plane and \Gamma is a collection...
uses
this notion of the
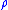 -length of curves and is useful in the study of
-length of curves and is useful in the study ofconformal mappings
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
.
Integration by parts
A function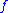 is said to be "regular" at a point
is said to be "regular" at a point  if the right and left hand limits
if the right and left hand limits 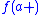 and
and  exist, and the function takes the average value,
exist, and the function takes the average value,
at the limiting point. Given two functions
 and
and  of finite variation, if at each point either
of finite variation, if at each point either  or
or  is continuous, or if both
is continuous, or if both  and
and  are regular, then there is an integration by parts
are regular, then there is an integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
formula for the Lebesgue–Stieltjes integral:

where
 . Under a slight generalization of this formula, the extra conditions on
. Under a slight generalization of this formula, the extra conditions on  and
and  can be dropped.
can be dropped.An alternative result, of significant importance in the theory of Stochastic calculus
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
is the following. Given two functions
 and
and  of finite variation, which are both right-continuous and have left-limits (they are cadlag
of finite variation, which are both right-continuous and have left-limits (they are cadlagCàdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
functions) then
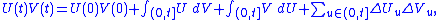
where
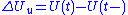 . This result can be seen as a precursor to Ito's lemma
. This result can be seen as a precursor to Ito's lemmaIto's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
, and is of use in the general theory of Stochastic integration. The final term is
 , which arises from the quadratic covariation of
, which arises from the quadratic covariation of  and
and  . (The earlier result can then be seen as a result pertaining to the Stratonovich integral
. (The earlier result can then be seen as a result pertaining to the Stratonovich integralStratonovich integral
In stochastic processes, the Stratonovich integral is a stochastic integral, the most common alternative to the Itō integral...
.)
Lebesgue integration
When g(x) = x for all real x, then μg is the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, and the Lebesgue–Stieltjes integral of f with respect to g is equivalent to the Lebesgue integral of f.
Riemann–Stieltjes integration and probability theory
Where f is a continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
real-valued function of a real variable and v is a non-decreasing real function, the Lebesgue–Stieltjes integral is equivalent to the Riemann–Stieltjes integral, in which case we often write
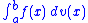
for the Lebesgue–Stieltjes integral, letting the measure μv remain implicit. This is particularly common in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
when v is the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a real-valued random variable X, in which case
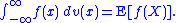
(See the article on Riemann–Stieltjes integration for more detail on dealing with such cases.)

