Log-Cauchy distribution
Encyclopedia
In probability theory, a log-Cauchy distribution is a probability distribution
of a random variable
whose logarithm
is distributed in accordance with a Cauchy distribution
. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.
:
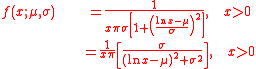
where
is a real number
and
. If 
is known, the scale parameter
is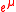
. 
and 
correspond to the location parameter
and scale parameter
of the associated Cauchy distribution. Some authors define
and 
as the location
and scale parameters, respectively, of the log-Cauchy distribution.
For
and 
, corresponding to a standard Cauchy distribution, the probability density function reduces to:
) when
and 
is:
when
and 
is:
and 
is: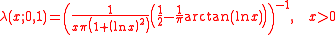
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.
. Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying
tail. As with the Cauchy distribution, none of the non-trivial moments
of the log-Cauchy distribution are finite. The mean
is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation
.
The log-Cauchy distribution is infinitely divisible
for some parameters but not for others. Like the lognormal distribution, log-t or log-Student distribution and Weibull distribution, the log-Cauchy distribution is a special case of the generalized beta distribution of the second kind. The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution. Logstable distributions have poles at x=0.
of the natural logarithm
s of a sample
is a robust estimator of
. The median absolute deviation
of the natural logarithms of a sample is a robust estimator of
.
, the log-Cauchy distribution can be used to approximate the improper Jeffreys
-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated. The log-Cauchy distribution can be used to model certain survival processes where significant outlier
s or extreme results may occur. An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV virus and showing symptoms of the disease, which may be very long for some people. It has also been proposed as a model for species abundance patterns.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
whose logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is distributed in accordance with a Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.
Probability density function
The log-Cauchy distribution has the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:
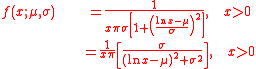
where
is a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and
. If is known, the scale parameterScale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
is
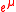. and correspond to the location parameterLocation parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
and scale parameter
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
of the associated Cauchy distribution. Some authors define
and as the locationLocation parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
and scale parameters, respectively, of the log-Cauchy distribution.
For
and , corresponding to a standard Cauchy distribution, the probability density function reduces to:Cumulative distribution function
The cumulative distribution function (cdfCDF
-Mathematics, science, and computers:* .cdf , the ANDI/netCDF mass spectrometry data interchange file format* Channel Definition Format, an XML standard* Charging Data Function, in the Session Initiation Protocol standard...
) when
and is:Survival function
The survival functionSurvival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
when
and is:Hazard rate
The hazard rate when and is: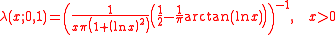The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.
Properties
The log-Cauchy distribution is an example of a heavy-tailed distributionHeavy-tailed distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
. Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying
Logarithmic growth
In mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. y = C log . Note that any logarithm base can be used, since one can be converted to another by a fixed constant...
tail. As with the Cauchy distribution, none of the non-trivial moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the log-Cauchy distribution are finite. The mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
The log-Cauchy distribution is infinitely divisible
Infinite divisibility (probability)
The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
for some parameters but not for others. Like the lognormal distribution, log-t or log-Student distribution and Weibull distribution, the log-Cauchy distribution is a special case of the generalized beta distribution of the second kind. The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution. Logstable distributions have poles at x=0.
Estimating parameters
The medianMedian
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
s of a sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
is a robust estimator of
. The median absolute deviationMedian absolute deviation
In statistics, the median absolute deviation is a robust measure of the variability of a univariate sample of quantitative data. It can also refer to the population parameter that is estimated by the MAD calculated from a sample....
of the natural logarithms of a sample is a robust estimator of
.Uses
In Bayesian statisticsBayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, the log-Cauchy distribution can be used to approximate the improper Jeffreys
Harold Jeffreys
Sir Harold Jeffreys, FRS was a mathematician, statistician, geophysicist, and astronomer. His seminal book Theory of Probability, which first appeared in 1939, played an important role in the revival of the Bayesian view of probability.-Biography:Jeffreys was born in Fatfield, Washington, County...
-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated. The log-Cauchy distribution can be used to model certain survival processes where significant outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s or extreme results may occur. An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV virus and showing symptoms of the disease, which may be very long for some people. It has also been proposed as a model for species abundance patterns.