
Logical matrix
Encyclopedia
A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0,1) matrix is a matrix
with entries from the Boolean domain
B = {0, 1}. Such a matrix can be used to represent a binary relation
between a pair of finite sets.
between the finite indexed sets X and Y (so ), then R can be represented by the adjacency matrix
M whose row and column indices index the elements of X and Y, respectively, such that the entries of M are defined by:
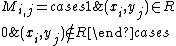
In order to designate the row and column numbers of the matrix, the sets X and Y are indexed with positive integers: i ranges from 1 to the cardinality of X and j ranges from 1 to the cardinality of Y. (See the entry on indexed sets for more detail.)
The corresponding representation as a Boolean matrix is:
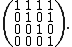
, that is, one whose entries on the diagonal are all 1, while the others are all 0.
If the Boolean domain is viewed as a semiring
, where addition corresponds to logical OR and multiplication to logical AND, the matrix representation of the composition
of two relations is equal to the matrix product of the matrix representations of these relation.
Frequently operations on binary matrices are defined in terms of modular arithmetic
mod 2 — that is, the elements are treated as elements of the Galois field GF(2) = ℤ2. They arise in a variety of representations and have a number of more restricted special forms.
The number of distinct m-by-n binary matrices is equal to 2mn, and is thus finite.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries from the Boolean domain
Boolean domain
In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
B = {0, 1}. Such a matrix can be used to represent a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
between a pair of finite sets.
Matrix representation of a relation
If R is a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
between the finite indexed sets X and Y (so ), then R can be represented by the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
M whose row and column indices index the elements of X and Y, respectively, such that the entries of M are defined by:
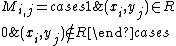
In order to designate the row and column numbers of the matrix, the sets X and Y are indexed with positive integers: i ranges from 1 to the cardinality of X and j ranges from 1 to the cardinality of Y. (See the entry on indexed sets for more detail.)
Example
The binary relation R on the set } is defined so that aRb holds if and only if a divides b evenly, with no remainder. For example, 2R4 holds because 2 divides 4 without leaving a remainder, but 3R4 does not hold because when 3 divides 4 there is a remainder of 1. The following set is the set of pairs for which the relation R holds.- {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.
The corresponding representation as a Boolean matrix is:
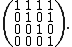
Other examples
- A permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
is a (0,1)-matrix, all of whose columns and rows each have exactly one nonzero element.- A Costas arrayCostas arrayIn mathematics, a Costas array can be regarded geometrically as a set of n points lying on the squares of a n×n checkerboard, such that each row or column contains only one point, and that all of the n/2 displacement vectors between each pair of dots are distinct...
is a special case of a permutation matrix
- A Costas array
- An incidence matrixIncidence matrixIn mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
in combinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and finite geometryFinite geometryA finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
has ones to indicate incidence between points (or vertices) and lines of a geometry, blocks of a block design, or edges of a graph (mathematics)Graph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges... - A design matrixDesign matrixIn statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
in analysis of varianceAnalysis of varianceIn statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
is a (0,1)-matrix with constant row sums. - An adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
in graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
is a matrix whose rows and columns represent the vertices and whose entries represent the edges of the graph. The adjacency matrix of a simple, undirected graph is a binary symmetric matrix with zero diagonal. - The biadjacency matrix of a simple, undirected bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
is a (0,1)-matrix, and any (0,1)-matrix arises in this way. - The prime factors of a list of m square-freeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, n-smoothSmooth numberIn number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
numbers can be described as a m×π(n) (0,1)-matrix, where π is the prime-counting function and aij is 1 if and only if the jth prime divides the ith number. This representation is useful in the quadratic sieveQuadratic sieveThe quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
factoring algorithm. - A bitmap imageRaster graphicsIn computer graphics, a raster graphics image, or bitmap, is a data structure representing a generally rectangular grid of pixels, or points of color, viewable via a monitor, paper, or other display medium...
containing pixelPixelIn digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s in only two colors can be represented as a (0,1)-matrix in which the 0's represent pixels of one color and the 1's represent pixels of the other color.
Some properties
The matrix representation of the equality relation on a finite set is an identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, that is, one whose entries on the diagonal are all 1, while the others are all 0.
If the Boolean domain is viewed as a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
, where addition corresponds to logical OR and multiplication to logical AND, the matrix representation of the composition
Composition of relations
In mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
of two relations is equal to the matrix product of the matrix representations of these relation.
Frequently operations on binary matrices are defined in terms of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
mod 2 — that is, the elements are treated as elements of the Galois field GF(2) = ℤ2. They arise in a variety of representations and have a number of more restricted special forms.
The number of distinct m-by-n binary matrices is equal to 2mn, and is thus finite.
See also
- List of matrices
- Redheffer matrixRedheffer matrixIn mathematics, a Redheffer matrix, studied by , is a matrix whose entries aij are 1 if i divides j or if j = 1; otherwise, aij = 0....

