
Lucas pseudoprime
Encyclopedia
In number theory
, the classes of Lucas pseudoprime and Fibonacci pseudoprime comprise sequences of composite
integers that passes certain tests that all prime
s pass: in this case, criteria relative to some Lucas sequence
.
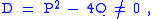
the Lucas sequences of the first and second kind, Un(P,Q) and Vn(P,Q) respectively, are defined by the recurrence relation
s



and


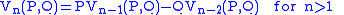
We can write
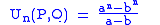

where a and b are roots of the auxiliary polynomial X2 - P X + Q,
of discriminant
D.
If p is an odd prime number
then
and if the Jacobi symbol
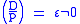 ,
,
then p is a factor of Up-ε.
(Riesel adds the condition that the Jacobi symbol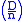 should be −1.)
should be −1.)
In the specific case of the Fibonacci sequence, where P = 1, Q = -1 and D = 5, the first Lucas pseudoprimes are 323 and 377;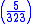 and
and 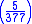 are both −1, the 324th Fibonacci number is a multiple of 323, and the 378th is a multiple of 377.
are both −1, the 324th Fibonacci number is a multiple of 323, and the 378th is a multiple of 377.
A strong Lucas pseudoprime is an odd composite number n with (n,D)=1, and n-ε=2rs with s odd, satisfying one of the conditions
for some j < r. A strong Lucas pseudoprime is also a Lucas pseudoprime.
An extra strong Lucas pseudoprime is a strong Lucas pseudoprime for a set of parameters (P,Q) where Q = 1, satisfying one of slightly modified conditions
for some j < r. An extra strong Lucas pseudoprime is also a strong Lucas pseudoprime.
By combining a Lucas pseudoprime test with a Fermat primality test
, say, to base 2, one can obtain very powerful probabilistic tests for primality. See the paper by Baillie and Wagstaff, and the books by Crandall and Riesel.
when Q = ±1.
A strong Fibonacci pseudoprime may be defined as a composite number which is a Fibonacci pseudoprime for all P. It follows (see Müller and Oswald) that in this case:
The smallest example of a strong Fibonacci pseudoprime is 443372888629441, which has factors 17, 31, 41, 43, 89, 97, 167 and 331.
It is conjectured that there are no even Fibonacci pseudoprimes (see Somer).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the classes of Lucas pseudoprime and Fibonacci pseudoprime comprise sequences of composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
integers that passes certain tests that all prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s pass: in this case, criteria relative to some Lucas sequence
Lucas sequence
In mathematics, the Lucas sequences Un and Vn are certain integer sequences that satisfy the recurrence relationwhere P and Q are fixed integers...
.
Definition
Given two integer parameters P and Q which satisfy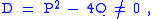
the Lucas sequences of the first and second kind, Un(P,Q) and Vn(P,Q) respectively, are defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s



and


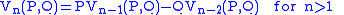
We can write
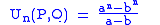

where a and b are roots of the auxiliary polynomial X2 - P X + Q,
of discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
D.
If p is an odd prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
then
- Vp is congruent to P modulo p.
and if the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
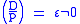 ,
,then p is a factor of Up-ε.
Lucas pseudoprimes
A Lucas pseudoprime is a composite number n for which n is a factor of Un-ε.(Riesel adds the condition that the Jacobi symbol
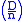 should be −1.)
should be −1.)In the specific case of the Fibonacci sequence, where P = 1, Q = -1 and D = 5, the first Lucas pseudoprimes are 323 and 377;
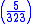 and
and 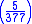 are both −1, the 324th Fibonacci number is a multiple of 323, and the 378th is a multiple of 377.
are both −1, the 324th Fibonacci number is a multiple of 323, and the 378th is a multiple of 377.A strong Lucas pseudoprime is an odd composite number n with (n,D)=1, and n-ε=2rs with s odd, satisfying one of the conditions
- n divides Us
- n divides V2js
for some j < r. A strong Lucas pseudoprime is also a Lucas pseudoprime.
An extra strong Lucas pseudoprime is a strong Lucas pseudoprime for a set of parameters (P,Q) where Q = 1, satisfying one of slightly modified conditions
- n divides Us and Vs is congruent to ±2 modulo n
- n divides V2js
for some j < r. An extra strong Lucas pseudoprime is also a strong Lucas pseudoprime.
By combining a Lucas pseudoprime test with a Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
, say, to base 2, one can obtain very powerful probabilistic tests for primality. See the paper by Baillie and Wagstaff, and the books by Crandall and Riesel.
Fibonacci pseudoprimes
A Fibonacci pseudoprime is a composite number n for which- Vn is congruent to P modulo n
when Q = ±1.
A strong Fibonacci pseudoprime may be defined as a composite number which is a Fibonacci pseudoprime for all P. It follows (see Müller and Oswald) that in this case:
- An odd composite integer n is also a Carmichael number
- 2(pi + 1) | (n − 1) or 2(pi + 1) | (n − pi) for every prime pi dividing n.
The smallest example of a strong Fibonacci pseudoprime is 443372888629441, which has factors 17, 31, 41, 43, 89, 97, 167 and 331.
It is conjectured that there are no even Fibonacci pseudoprimes (see Somer).
External links
- Anderson, Peter G. Fibonacci Pseudoprimes, their factors, and their entry points.
- Anderson, Peter G. Fibonacci Pseudoprimes under 2,217,967,487 and their factors.

