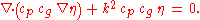Mild-slope equation
Encyclopedia
In fluid dynamics
, the mild-slope equation describes the combined effects of diffraction
and refraction
for water waves propagating over bathymetry
and due to lateral boundaries—like breakwater
s and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coast
s.
The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliff
s, beach
es, seawall
s and breakwaters. As a result, it describes the variations in wave amplitude
, or equivalently wave height
. From the wave amplitude, the amplitude of the flow velocity
oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to determine the wave effects on coastal and offshore structures, ships and other floating objects, sediment transport
and resulting geomorphology
changes of the sea bed and coastline, mean flow fields and mass transfer
of dissolved and floating materials. Most often, the mild-slope equation is solved by computer using methods from numerical analysis
.
A first form of the mild-slope equation was developed by Eckart
in 1952, and an improved version—the mild-slope equation in its classical formulation—has been derived independently by Juri Berkhoff in 1972. Thereafter, many modified and extended forms have been proposed, to include the effects of, for instance: wave–current interaction
, wave nonlinearity
, steeper sea-bed slopes, bed friction
and wave breaking. Also parabolic
approximations to the mild-slope equation are often used, in order to reduce the computational cost.
In case of a constant depth, the mild-slope equation reduces to the Helmholtz equation
for wave diffraction.
elevation given as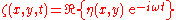 and the waves propagating on a fluid layer of mean
and the waves propagating on a fluid layer of mean
water depth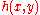 —the mild-slope equation is:
—the mild-slope equation is:
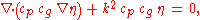
where:
The phase and group speed depend on the dispersion relation
, and are derived from Airy wave theory
as:
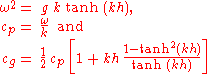
where
For a given angular frequency , the wavenumber
, the wavenumber 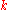 has to be solved from the dispersion equation, which relates these two quantities to the water depth
has to be solved from the dispersion equation, which relates these two quantities to the water depth 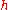 .
.
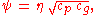
the mild slope equation can be cast in the form of an inhomogeneous Helmholtz equation:

where is the Laplace operator
is the Laplace operator
.
fields of propagating waves, it is useful to split the complex amplitude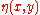 in its amplitude and phase, both real value
in its amplitude and phase, both real value
d:
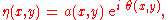
where
This transforms the mild-slope equation in the following set of equations (apart from locations for which is singular):
is singular):
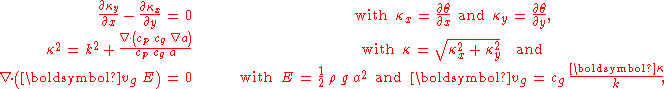
where
The last equation shows that wave energy is conserved in the mild-slope equation, and that the wave energy is transported in the
is transported in the  -direction normal to the wave crest
-direction normal to the wave crest
s (in this case of pure wave motion without mean currents). The effective group speed is different from the group speed
is different from the group speed 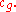
The first equation states that the effective wavenumber is irrotational, a direct consequence of the fact it is the derivative of the wave phase
is irrotational, a direct consequence of the fact it is the derivative of the wave phase 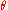 , a scalar field
, a scalar field
. The second equation is the eikonal equation
. It shows the effects of diffraction on the effective wavenumber: only for more-or-less progressive waves, with the splitting into amplitude
the splitting into amplitude  and phase
and phase 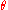 leads to consistent-varying and meaningful fields of
leads to consistent-varying and meaningful fields of  and
and  . Otherwise, κ2 can even become negative. When the diffraction effects are totally neglected, the effective wavenumber κ is equal to
. Otherwise, κ2 can even become negative. When the diffraction effects are totally neglected, the effective wavenumber κ is equal to 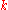 , and the geometric optics approximation for wave refraction
, and the geometric optics approximation for wave refraction
can be used.
When is used in the mild-slope equation, the result is, apart from a factor
is used in the mild-slope equation, the result is, apart from a factor 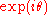 :
:

Now both the real part and the imaginary part of this equation have to be equal to zero:
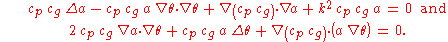
The effective wavenumber vector is defined as the gradient of the wave phase:
is defined as the gradient of the wave phase:
 and its vector length is
and its vector length is 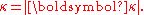
Note that is an irrotational field, since the curl of the gradient is zero:
is an irrotational field, since the curl of the gradient is zero:

Now the real and imaginary parts of the transformed mild-slope equation become, first multiplying the imaginary part by :
:
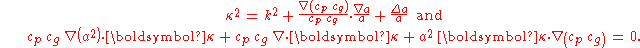
The first equation directly leads to the eikonal equation above for , while the second gives:
, while the second gives:
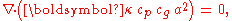
which—by noting that in which the angular frequency
in which the angular frequency  is a constant for time-harmonic
is a constant for time-harmonic
motion—leads to the wave-energy conservation equation.
and incompressible, and the flow is assumed to be irrotational. These assumptions are valid ones for surface gravity waves, since the effects of vorticity and viscosity
are only significant in the Stokes boundary layer
s (for the oscillatory part of the flow). Because the flow is irrotational, the wave motion can be described using potential flow
theory.
formulation gives a variational formulation for non-linear surface gravity waves.
For the case of a horizontally unbounded domain with a constant density
 , a free fluid surface at
, a free fluid surface at 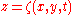 and a fixed sea bed at
and a fixed sea bed at 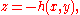 Luke's variational principle
Luke's variational principle  uses the Lagrangian
uses the Lagrangian
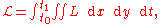
where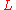 is the horizontal Lagrangian density, given by:
is the horizontal Lagrangian density, given by:
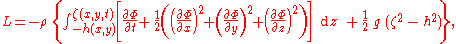
where is the velocity potential, with the flow velocity
is the velocity potential, with the flow velocity
components being
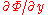 and
and 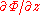 in the
in the  ,
, 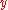 and
and  directions, respectively.
directions, respectively.
Luke's Lagrangian formulation can also be recast into a Hamiltonian formulation
in terms of the surface elevation and velocity potential at the free surface.
Taking the variations of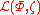 with respect to the potential
with respect to the potential 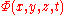 and surface elevation
and surface elevation  leads to the Laplace equation for
leads to the Laplace equation for 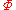 in the fluid interior, as well as all the boundary conditions both on the free surface
in the fluid interior, as well as all the boundary conditions both on the free surface 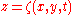 as at the bed at
as at the bed at 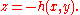
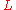 is split into a part from the bed
is split into a part from the bed 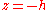 to the mean surface at
to the mean surface at  and a second part from
and a second part from  to the free surface
to the free surface  . Using a Taylor series
. Using a Taylor series
expansion for the second integral around the mean free-surface elevation and only retaining quadratic terms in
and only retaining quadratic terms in  and
and 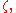 the Lagrangian density
the Lagrangian density 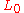 for linear wave motion becomes
for linear wave motion becomes
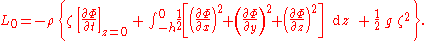
The term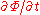 in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equations, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to
in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equations, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to 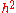 in the potential energy.
in the potential energy.
The waves propagate in the horizontal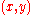 plane, while the structure of the potential
plane, while the structure of the potential 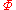 is not wave-like in the vertical
is not wave-like in the vertical  -direction. This suggests the use of the following assumption on the form of the potential
-direction. This suggests the use of the following assumption on the form of the potential 
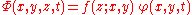 with normalisation
with normalisation 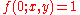 at the mean free-surface elevation
at the mean free-surface elevation 
Here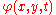 is the velocity potential at the mean free-surface level
is the velocity potential at the mean free-surface level  Next, the mild-slope assumption is made, in that the vertical shape function
Next, the mild-slope assumption is made, in that the vertical shape function  changes slowly in the
changes slowly in the  -plane, and horizontal derivatives of
-plane, and horizontal derivatives of  can be neglected in the flow velocity. So:
can be neglected in the flow velocity. So:
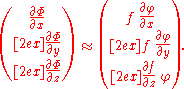
As a result:
 with
with 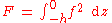 and
and 
The Euler–Lagrange equations for this Lagrangian density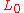 are, with
are, with 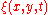 representing either
representing either 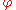 or
or 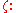
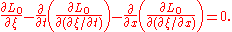
Now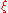 is first taken equal to
is first taken equal to 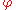 and then to
and then to 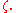
As a result, the evolution equations for the wave motion become:

The next step is to choose the shape function and to determine
and to determine  and
and 
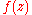 is chosen according to Airy wave theory
is chosen according to Airy wave theory
. This is the linear theory of waves propagating in constant depth The form of the shape function is:
The form of the shape function is:
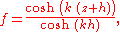
with now in general not a constant, but chosen to vary with
now in general not a constant, but chosen to vary with  and
and  according to the local depth
according to the local depth 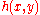 and the linear dispersion relation:
and the linear dispersion relation:

Here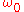 a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals
a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals  and
and  become:
become:

The following time-dependent equations give the evolution of the free-surface elevation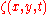 and free-surface potential
and free-surface potential 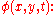
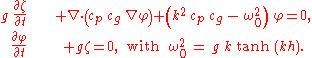
From the two evolution equations, one of the variables or
or  can be eliminated, to obtain the time-dependent form of the mild-slope equation:
can be eliminated, to obtain the time-dependent form of the mild-slope equation:
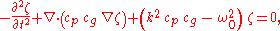
and the corresponding equation for the free-surface potential is identical, with replaced by
replaced by  The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies around
The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies around 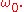
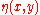 and angular frequency
and angular frequency 
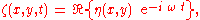
with and
and 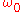 chosen equal to each other,
chosen equal to each other, 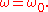 Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion:
Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion:
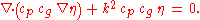
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the mild-slope equation describes the combined effects of diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
and refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
for water waves propagating over bathymetry
Bathymetry
Bathymetry is the study of underwater depth of lake or ocean floors. In other words, bathymetry is the underwater equivalent to hypsometry. The name comes from Greek βαθύς , "deep", and μέτρον , "measure"...
and due to lateral boundaries—like breakwater
Breakwater (structure)
Breakwaters are structures constructed on coasts as part of coastal defence or to protect an anchorage from the effects of weather and longshore drift.-Purposes of breakwaters:...
s and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coast
Coast
A coastline or seashore is the area where land meets the sea or ocean. A precise line that can be called a coastline cannot be determined due to the dynamic nature of tides. The term "coastal zone" can be used instead, which is a spatial zone where interaction of the sea and land processes occurs...
s.
The mild-slope equation models the propagation and transformation of water waves, as they travel through waters of varying depth and interact with lateral boundaries such as cliff
Cliff
In geography and geology, a cliff is a significant vertical, or near vertical, rock exposure. Cliffs are formed as erosion landforms due to the processes of erosion and weathering that produce them. Cliffs are common on coasts, in mountainous areas, escarpments and along rivers. Cliffs are usually...
s, beach
Beach
A beach is a geological landform along the shoreline of an ocean, sea, lake or river. It usually consists of loose particles which are often composed of rock, such as sand, gravel, shingle, pebbles or cobblestones...
es, seawall
Seawall
A seawall is a form of coastal defence constructed where the sea, and associated coastal processes, impact directly upon the landforms of the coast. The purpose of a seawall is to protect areas of human habitation, conservation and leisure activities from the action of tides and waves...
s and breakwaters. As a result, it describes the variations in wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
, or equivalently wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
. From the wave amplitude, the amplitude of the flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
oscillations underneath the water surface can also be computed. These quantities—wave amplitude and flow-velocity amplitude—may subsequently be used to determine the wave effects on coastal and offshore structures, ships and other floating objects, sediment transport
Sediment transport
Sediment transport is the movement of solid particles , typically due to a combination of the force of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained...
and resulting geomorphology
Geomorphology
Geomorphology is the scientific study of landforms and the processes that shape them...
changes of the sea bed and coastline, mean flow fields and mass transfer
Mass transfer
Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...
of dissolved and floating materials. Most often, the mild-slope equation is solved by computer using methods from numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
.
A first form of the mild-slope equation was developed by Eckart
Carl Eckart
Carl Henry Eckart was an American physicist, physical oceanographer, geophysicist, and administrator. He co-developed the Wigner-Eckart theorem and is also known for the Eckart conditions in quantum mechanics.-Education:Eckart began college in 1919 at Washington University in St...
in 1952, and an improved version—the mild-slope equation in its classical formulation—has been derived independently by Juri Berkhoff in 1972. Thereafter, many modified and extended forms have been proposed, to include the effects of, for instance: wave–current interaction
Wave–current interaction
In fluid dynamics, wave–current interaction is the interaction between surface gravity waves and a mean flow. The interaction implies an exchange of energy, so after the start of the interaction both the waves and the mean flow are affected....
, wave nonlinearity
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
, steeper sea-bed slopes, bed friction
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
and wave breaking. Also parabolic
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
approximations to the mild-slope equation are often used, in order to reduce the computational cost.
In case of a constant depth, the mild-slope equation reduces to the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
for wave diffraction.
Formulation for monochromatic wave motion
For monochromatic waves according to linear theory—with the free surfaceFree surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
elevation given as
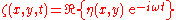 and the waves propagating on a fluid layer of mean
and the waves propagating on a fluid layer of meanAverage
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
water depth
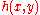 —the mild-slope equation is:
—the mild-slope equation is: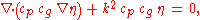
where:
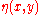 is the complex-valuedComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
is the complex-valuedComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the free-surface elevation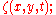
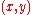 is the horizontal position;
is the horizontal position; is the angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
is the angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the monochromatic wave motion;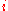 is the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
is the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
;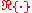 means taking the real part of the quantity between braces;
means taking the real part of the quantity between braces; is the horizontal gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is the horizontal gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator; is the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
is the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator; is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
;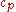 is the phase speed of the waves and
is the phase speed of the waves and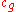 is the group speed of the waves.
is the group speed of the waves.
The phase and group speed depend on the dispersion relation
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
, and are derived from Airy wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
as:
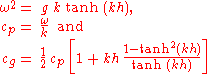
where
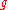 is Earth's gravityEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
is Earth's gravityEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
and is the hyperbolic tangent.
is the hyperbolic tangent.
For a given angular frequency
 , the wavenumber
, the wavenumber 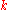 has to be solved from the dispersion equation, which relates these two quantities to the water depth
has to be solved from the dispersion equation, which relates these two quantities to the water depth 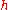 .
.Transformation to an inhomogeneous Helmholtz equation
Through the transformation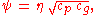
the mild slope equation can be cast in the form of an inhomogeneous Helmholtz equation:

where
 is the Laplace operator
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
Propagating waves
In spatially coherentCoherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
fields of propagating waves, it is useful to split the complex amplitude
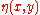 in its amplitude and phase, both real value
in its amplitude and phase, both real valueReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
d:
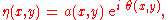
where
 is the amplitude or absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
is the amplitude or absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of and
and is the wave phase, which is the argumentArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
is the wave phase, which is the argumentArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
of
This transforms the mild-slope equation in the following set of equations (apart from locations for which
 is singular):
is singular):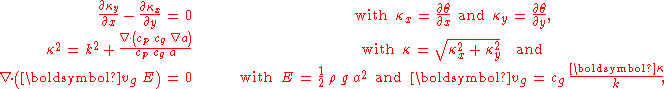
where
-
 is the averageAverageIn mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
is the averageAverageIn mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
wave-energy density per unit horizontal area (the sum of the kineticKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energyPotential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
densities), -
 is the effective wavenumber vector, with components
is the effective wavenumber vector, with components 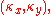
-
 is the effective group velocityGroup velocityThe group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
is the effective group velocityGroup velocityThe group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
vector, -
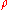 is the fluid densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
is the fluid densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, and -
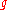 is the acceleration by the Earth's gravityEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
is the acceleration by the Earth's gravityEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
.
The last equation shows that wave energy is conserved in the mild-slope equation, and that the wave energy
 is transported in the
is transported in the  -direction normal to the wave crest
-direction normal to the wave crestCrest (physics)
A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
s (in this case of pure wave motion without mean currents). The effective group speed
 is different from the group speed
is different from the group speed 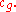
The first equation states that the effective wavenumber
 is irrotational, a direct consequence of the fact it is the derivative of the wave phase
is irrotational, a direct consequence of the fact it is the derivative of the wave phase 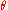 , a scalar field
, a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. The second equation is the eikonal equation
Eikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
. It shows the effects of diffraction on the effective wavenumber: only for more-or-less progressive waves, with
 the splitting into amplitude
the splitting into amplitude  and phase
and phase 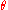 leads to consistent-varying and meaningful fields of
leads to consistent-varying and meaningful fields of  and
and  . Otherwise, κ2 can even become negative. When the diffraction effects are totally neglected, the effective wavenumber κ is equal to
. Otherwise, κ2 can even become negative. When the diffraction effects are totally neglected, the effective wavenumber κ is equal to 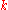 , and the geometric optics approximation for wave refraction
, and the geometric optics approximation for wave refractionRefraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
can be used.
When
 is used in the mild-slope equation, the result is, apart from a factor
is used in the mild-slope equation, the result is, apart from a factor 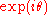 :
:
Now both the real part and the imaginary part of this equation have to be equal to zero:
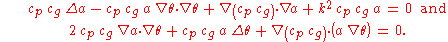
The effective wavenumber vector
 is defined as the gradient of the wave phase:
is defined as the gradient of the wave phase: and its vector length is
and its vector length is 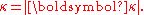
Note that
 is an irrotational field, since the curl of the gradient is zero:
is an irrotational field, since the curl of the gradient is zero:
Now the real and imaginary parts of the transformed mild-slope equation become, first multiplying the imaginary part by
 :
: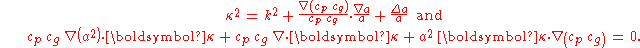
The first equation directly leads to the eikonal equation above for
 , while the second gives:
, while the second gives: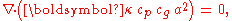
which—by noting that
 in which the angular frequency
in which the angular frequency  is a constant for time-harmonic
is a constant for time-harmonicHarmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
motion—leads to the wave-energy conservation equation.
Derivation of the mild-slope equation
The mild-slope equation can be derived by the use of several methods. Here, we will use a variational approach. The fluid is assumed to be inviscidViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and incompressible, and the flow is assumed to be irrotational. These assumptions are valid ones for surface gravity waves, since the effects of vorticity and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
are only significant in the Stokes boundary layer
Stokes boundary layer
In fluid dynamics, the Stokes boundary layer, or oscillatory boundary layer, refers to the boundary layer close to a solid wall in oscillatory flow of a viscous fluid...
s (for the oscillatory part of the flow). Because the flow is irrotational, the wave motion can be described using potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory.
Luke's variational principle
Luke's LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
formulation gives a variational formulation for non-linear surface gravity waves.
For the case of a horizontally unbounded domain with a constant density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
 , a free fluid surface at
, a free fluid surface at 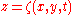 and a fixed sea bed at
and a fixed sea bed at 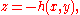 Luke's variational principle
Luke's variational principle  uses the Lagrangian
uses the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
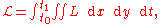
where
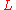 is the horizontal Lagrangian density, given by:
is the horizontal Lagrangian density, given by: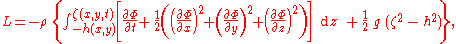
where
 is the velocity potential, with the flow velocity
is the velocity potential, with the flow velocityFlow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
components being

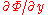 and
and 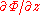 in the
in the  ,
, 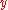 and
and  directions, respectively.
directions, respectively.Luke's Lagrangian formulation can also be recast into a Hamiltonian formulation
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
in terms of the surface elevation and velocity potential at the free surface.
Taking the variations of
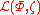 with respect to the potential
with respect to the potential 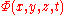 and surface elevation
and surface elevation  leads to the Laplace equation for
leads to the Laplace equation for 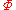 in the fluid interior, as well as all the boundary conditions both on the free surface
in the fluid interior, as well as all the boundary conditions both on the free surface 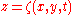 as at the bed at
as at the bed at 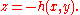
Linear wave theory
In case of linear wave theory, the vertical integral in the Lagrangian density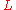 is split into a part from the bed
is split into a part from the bed 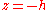 to the mean surface at
to the mean surface at  and a second part from
and a second part from  to the free surface
to the free surface  . Using a Taylor series
. Using a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion for the second integral around the mean free-surface elevation
 and only retaining quadratic terms in
and only retaining quadratic terms in  and
and 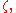 the Lagrangian density
the Lagrangian density 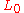 for linear wave motion becomes
for linear wave motion becomes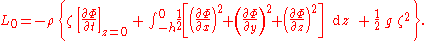
The term
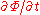 in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equations, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to
in the vertical integral is dropped since it has become dynamically uninteresting: it gives a zero contribution to the Euler–Lagrange equations, with the upper integration limit now fixed. The same is true for the neglected bottom term proportional to 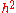 in the potential energy.
in the potential energy.The waves propagate in the horizontal
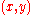 plane, while the structure of the potential
plane, while the structure of the potential 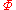 is not wave-like in the vertical
is not wave-like in the vertical  -direction. This suggests the use of the following assumption on the form of the potential
-direction. This suggests the use of the following assumption on the form of the potential 
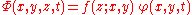 with normalisation
with normalisation 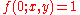 at the mean free-surface elevation
at the mean free-surface elevation 
Here
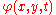 is the velocity potential at the mean free-surface level
is the velocity potential at the mean free-surface level  Next, the mild-slope assumption is made, in that the vertical shape function
Next, the mild-slope assumption is made, in that the vertical shape function  changes slowly in the
changes slowly in the  -plane, and horizontal derivatives of
-plane, and horizontal derivatives of  can be neglected in the flow velocity. So:
can be neglected in the flow velocity. So: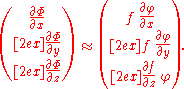
As a result:
 with
with 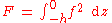 and
and 
The Euler–Lagrange equations for this Lagrangian density
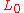 are, with
are, with 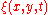 representing either
representing either 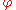 or
or 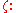
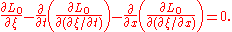
Now
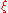 is first taken equal to
is first taken equal to 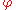 and then to
and then to 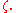
As a result, the evolution equations for the wave motion become:

The next step is to choose the shape function
 and to determine
and to determine  and
and 
Vertical shape function from Airy wave theory
Since the objective is the description of waves over mildly sloping beds, the shape function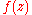 is chosen according to Airy wave theory
is chosen according to Airy wave theoryAiry wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
. This is the linear theory of waves propagating in constant depth
 The form of the shape function is:
The form of the shape function is: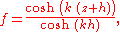
with
 now in general not a constant, but chosen to vary with
now in general not a constant, but chosen to vary with  and
and  according to the local depth
according to the local depth 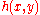 and the linear dispersion relation:
and the linear dispersion relation:
Here
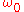 a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals
a constant angular frequency, chosen in accordance with the characteristics of the wave field under study. Consequently, the integrals  and
and  become:
become:
The following time-dependent equations give the evolution of the free-surface elevation
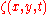 and free-surface potential
and free-surface potential 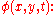
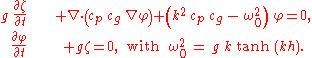
From the two evolution equations, one of the variables
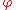 or
or  can be eliminated, to obtain the time-dependent form of the mild-slope equation:
can be eliminated, to obtain the time-dependent form of the mild-slope equation: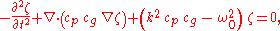
and the corresponding equation for the free-surface potential is identical, with
 replaced by
replaced by  The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies around
The time-dependent mild-slope equation can be used to model waves in a narrow band of frequencies around 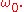
Monochromatic waves
Consider monochromatic waves with complex amplitude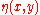 and angular frequency
and angular frequency 
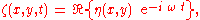
with
 and
and 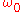 chosen equal to each other,
chosen equal to each other, 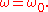 Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion:
Using this in the time-dependent form of the mild-slope equation, recovers the classical mild-slope equation for time-harmonic wave motion: