Nordström's theory of gravitation
Encyclopedia
In theoretical physics
, Nordström's theory of gravitation was a predecessor of general relativity
. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström
, in 1912 and 1913 respectively. The first was quickly dismissed, but the second became the first known example of a metric theory of gravitation
, in which the effects of gravitation are treated entirely in terms of the geometry of a curved spacetime
.
Neither of Nordström's theories are in agreement with observation and experiment. Nonetheless, the first remains of interest insofar as it led to the second. The second remains of interest both as an important milestone on the road to the current theory of gravitation, general relativity
, and as a simple example of a self-consistent relativistic theory of gravitation. As an example, this theory is particularly useful in the context of pedagogical discussions of how to derive and test the predictions of a metric theory of gravitation.
, Max Abraham
in Milan
, Gustav Mie
in Greifswald
, Germany, and Albert Einstein
in Prague
, were all trying to create competing relativistic theories of gravitation.
All of these researchers began by trying to suitably modify the existing theory, the field theory
version of Newton's theory of gravitation. In this theory, the field equation
is the Poisson equation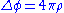
, where 
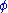is the gravitational potential and 
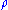is the density of matter, augmented by an equation of motion for a test particle
in an ambient gravitational field, which we can derive from
Newton's force law and which states that the acceleration
of the test particle is given by the gradient of the potential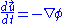
This theory is not relativistic because the equation of motion refers to coordinate time rather than proper time
, and because, should the matter in some isolated object suddenly be redistributed by an explosion, the field equation requires that the potential everywhere in "space" must be "updated" instantaneously, which violates the principle that any "news" which has a physical effect (in this case, an effect on test particle
motion far from the source of the field) cannot be transmitted faster than the speed of light
. Einstein's former calculus professor, Hermann Minkowski
had sketched a vector theory of gravitation as early as 1908, but in 1912, Abraham pointed out that no such theory would admit stable planetary orbits. This was one reason why Nordström turned to scalar theories of gravitation (while Einstein explored tensor theories).
Nordström's first attempt to propose a suitable relativistic scalar field equation of gravitation was the simplest and most natural choice imaginable: simply replace the Laplacian in the Newtonian field equation with the D'Alembertian or wave operator, which gives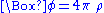
. This has the result of changing the vacuum field equation from the Laplace equation to the wave equation
, which means that any "news" concerning redistribution of matter in one location is transmitted at the speed of light to other locations. Correspondingly, the simplest guess for a suitable equation of motion for test particles might seem to be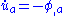
where the dot signifies differentiation with respect to proper time and where 
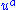is the velocity four-vector of the test particle. This force law had earlier been proposed by Abraham, and Nordström knew that it wouldn't work. Instead he proposed 
.
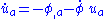However, this theory is unacceptable for a variety of reasons. Two objections are theoretical. First, this theory is not derivable from a Lagrangian
, unlike the Newtonian field theory (or most metric theories of gravitation). Second, the proposed field equation is linear. But by analogy with electromagnetism
, we should expect the gravitational field to carry energy, and on the basis of Einstein's work on relativity theory, we should expect this energy to be equivalent to mass and therefore, to gravitate. This implies that the field equation should be nonlinear. Another objection is more practical: this theory disagrees drastically with observation.
Einstein and von Laue proposed that the problem might lie with the field equation, which, they suggested, should have the linear form
, where F is some yet unknown function of 
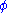, and where Tmatter is the trace
of the stress-energy tensor
describing the density, momentum, and stress of any matter present.
In response to these criticisms, Nordström proposed his second theory in 1913. From the proportionality of inertial and gravitational mass, he deduced that the field equation should be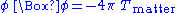
, which is nonlinear. Nordström now took the equation of motion to be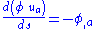
or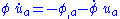
.
Einstein took the first opportunity to proclaim his approval of the new theory. In a keynote address to the annual meeting of the Society of German Scientists and Physicians, given in Vienna
on September 23, 1913, Einstein surveyed the state of the art, declaring that only his own work with Marcel Grossmann
and the second theory of Nordström were worthy of consideration. (Mie, who was in the audience, rose to protest, but Einstein explained his criteria and Mie was forced to admit that his own theory did not meet them.) Einstein considered the special case when the only matter present is a cloud of dust (that is, a perfect fluid
in which the pressure is assumed to be negligible). He argued that the contribution of this matter to the stress-energy tensor should be: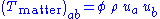
He then derived an expression for the stress-energy tensor of the gravitational field in Nordström's second theory,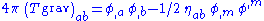
which he proposed should hold in general, and showed that the sum of the contributions to the stress-energy tensor from the gravitational field energy and from matter would be conserved, as should be the case. Furthermore, he showed, the field equation of Nordström's second theory follows from the Lagrangian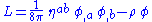
Since Nordström's equation of motion for test particles in an ambient gravitational field also follows from a Lagrangian, this shows that Nordström's second theory can be derived from an action principle and also shows that it obeys other properties we must demand from a self-consistent field theory.
Meanwhile, a gifted Dutch student, Adriaan Fokker
had written a Ph.D. thesis under Hendrik Lorentz
in which he derived what is now called the Fokker-Planck equation
. Lorentz, delighted by his former student's success, arranged for Fokker to pursue post-doctoral study with Einstein in Prague. The result was a historic paper which appeared in 1914, in which Einstein and Fokker observed that the Lagrangian for Nordström's equation of motion for test particles,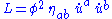
, is the geodesic Lagrangian for a curved Lorentzian manifold with metric tensor
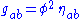. If we adopt Cartesian coordinates with line element 
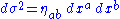with corresponding wave operator 
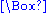on the flat background, or Minkowski spacetime, so that the line element of the curved spacetime is 
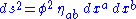, then the Ricci scalar of this curved spacetime is just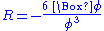
Therefore Nordström's field equation becomes simply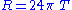
where on the right hand side, we have taken the trace of the stress-energy tensor (with contributions from matter plus any non-gravitational fields) using the metric tensor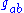
. This is a historic result, because here for the first time we have a field equation in which on the left hand side stands a purely geometrical quantity (the Ricci scalar is the trace of the Ricci tensor, which is itself a kind of trace of the fourth rank Riemann curvature tensor
), and on the right hand stands a purely physical quantity, the trace of the stress-energy tensor. Einstein gleefully pointed out that this equation now takes the form which he had earlier proposed with von Laue, and gives a concrete example of a class of theories which he had studied with Grossmann.
Some time latter, Hermann Weyl
introduced the Weyl curvature tensor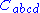
, which measures the deviation of a Lorentzian manifold from being conformally flat, i.e. with metric tensor having the form of the product of some scalar function with the metric tensor of flat spacetime. This is exactly the special form of the metric proposed in Nordström's second theory, so the entire content of this theory can be even more elegantly summarized in the following two equations:
We can immediately write down the general vacuum solution in Nordström's theory: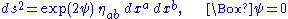
where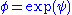
and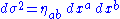 
is the line element for flat spacetime in any convenient coordinate chart (such as cylindrical, polar spherical, or double null coordinates), and where 
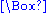is the ordinary wave operator on flat spacetime (expressed in cylindrical, polar spherical, or double null coordinates, respectively). But the general solution of the ordinary three dimensional wave equation is well known, and can be given rather explicit form. Specifically, for certain charts such as cylindrical or polar spherical charts on flat spacetime (which induce corresponding charts on our curved Lorentzian manifold), we can write the general solution in terms of a power series, and we can write the general solution of certain Cauchy problem
s in the manner familiar from the Lienard-Wiechert potentials in electromagnetism.
In any solution to Nordström's field equations (vacuum or otherwise), if we consider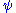
as controlling a conformal perturbation from flat spacetime, then to first order in 
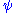we have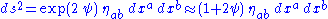
Thus, in the weak field approximation, we can identify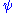
with the Newtonian gravitational potential, and we can regard it as controlling a small conformal perturbation from a flat spacetime background.
In any metric theory of gravitation, all gravitational effects arise from the curvature of the metric. In a spacetime model in Nordström's theory (but not in general relativity), this depends only on the trace of the stress-energy tensor. But the field energy of an electromagnetic field contributes a term to the stress-energy tensor which is traceless, so in Nordström's theory, electromagnetic field energy does not gravitate! Indeed, since every solution to the field equations of this theory is a spacetime which is among other things conformally equivalent to flat spacetime, null geodesics must agree with the null geodesics of the flat background, so this theory can exhibit no light bending.
Incidentally, the fact that the trace of the stress-energy tensor for an electrovacuum solution
(a solution in which there is no matter present, nor any non-gravitational fields except for an electromagnetic field) vanishes shows that in the general electrovacuum solution in Nordström's theory, the metric tensor has the same form as in a vacuum solution, so we need only write down and solve the curved spacetime Maxwell field equations
. But these are conformally invariant, so we can also write down the general electrovacuum solution, say in terms of a power series.
In any Lorentzian manifold (with appropriate tensor fields describing any matter and physical fields) which stands as a solution to Nordström's field equations, the conformal part of the Riemann tensor (i.e. the Weyl tensor) always vanishes. The Ricci scalar also vanishes identically in any vacuum region (or even, any region free of matter but containing an electromagnetic field). Are there any further restrictions on the Riemann tensor in Nordström's theory?
To find out, note that an important identity from the theory of manifolds, the Ricci decomposition
, splits the Riemann tensor into three pieces, which are each fourth-rank tensors, built out of, respectively, the Ricci scalar, the trace-free Ricci tensor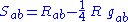
and the Weyl tensor
. It immediately follows that Nordström's theory leaves the trace-free Ricci tensor entirely unconstrained by algebraic relations (other than the symmetric property, which this second rank tensor always enjoys). But taking account of the twice-contracted and detraced Bianchi identity, a differential identity which holds for the Riemann tensor in any (semi)-Riemannian manifold
, we see that in Nordström's theory, as a consequence of the field equations, we have the first-order covariant differential equation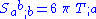
which constrains the semi-traceless part of the Riemann tensor (the one built out of the trace-free Ricci tensor).
Thus, according to Nordström's theory, in a vacuum region only the semi-traceless part of the Riemann tensor can be nonvanishing. Then our covariant differential constraint on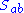
shows how variations in the trace of the stress-energy tensor in our spacetime model can generate a nonzero trace-free Ricci tensor, and thus nonzero semi-traceless curvature, which can propagate into a vacuum region. This is critically important, because otherwise gravitation would not, according to this theory, be a long-range force capable of propagating through a vacuum.
In general relativity, something somewhat analogous happens, but there it is the Ricci tensor which vanishes in any vacuum region (but not in a region which is matter-free but contains an electromagnetic field), and it is the Weyl curvature which is generated (via another first order covariant differential equation) by variations in the stress-energy tensor and which then propagates into vacuum regions, rendering gravitation a long-range force capable of propagating through a vacuum.
We can tabulate the most basic differences between Nordström's theory and general relativity, as follows:
Another very striking feature of Nordström's theory is that it while it can be written as the theory of a certain scalar field in Minkowski spacetime, and in this form enjoys the expected conservation law for nongravitational mass-energy together with gravitational field energy, but suffers from a not very memorable force law, in the curved spacetime formulation the motion of test particles is very elegantly described (the world line of a free test particle is a timelike geodesic, and by an obvious limit, the world line of a laser pulse is a null geodesic), but we lose the conservation law. So which interpretation is correct? In other words, which metric is the one which according to Nordström can be measured locally by physical experiments? The answer is: the curved spacetime is the physically observable one in this theory (as in all metric theories of gravitation); the flat background is a mere mathematical fiction which is however of inestimable value for such purposes as writing down the general vacuum solution, or studying the weak field limit.
At this point, we could show that in the limit of slowly moving test particles and slowly evolving weak gravitational fields, Nordström's theory of gravitation reduces to the Newtonian theory of gravitation. Rather than showing this in detail, we will proceed to a detailed study the two most important solutions in this theory:
We will use the first to obtain the predictions of Nordström's theory for the four classic solar system tests of relativistic gravitation theories (in the ambient field of an isolated spherically symmetric object), and we will use the second to compare gravitational radiation in Nordström's theory and in Einstein's general theory of relativity.
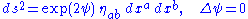
where we can take the flat spacetime Laplace operator on the right. To first order in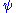
, the metric becomes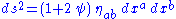
where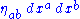
is the metric of Minkowski spacetime (the flat background).
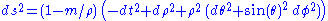
where we justify our choice of integration constants by the fact that this is the unique choice giving the correct Newtonian limit. This gives the solution in terms of coordinates which directly exhibit the fact that this spacetime is conformally equivalent to Minkowski spacetime, but the radial coordinate in this chart does not readily admit a direct geometric interpretation. Therefore, we adopt instead Schwarzschild coordinates, using the transformation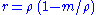
, which brings the metric into the form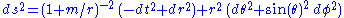
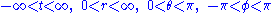
Here, r now has the simple geometric interpretation that the surface area of the coordinate sphere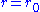
is just 
.
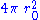Just as happens in the corresponding static spherically symmetric asymptotically flat solution of general relativity, this solution admits a four dimensional Lie group
of isometries, or equivalently, a four dimensional (real) Lie algebra
of Killing vector fields. These are readily determined to be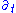
(translation in time)
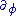(rotation about an axis through the origin)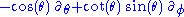
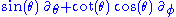
These are exactly the same vector fields which arise in the Schwarzschild coordinate chart for the Schwarzschild vacuum solution
of general relativity, and they simply express the fact that this spacetime is static and spherically symmetric.
If we set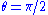
we find that test particle motion confined to the equatorial plane is possible, and in this case first integrals (first order ordinary differential equations) are readily obtained. First, we have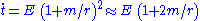
where to first order in m we have the same result as for the Schwarzschild vacuum. This also shows that Nordström's theory agrees with the result of the Pound-Rebka experiment
. Second, we have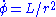
which is the same result as for the Schwarzschild vacuum. This expresses conservation of orbital anglar momentum of test particles moving in the equatorial plane, and shows that the period of a nearly circular orbit (as observed by a distant observer) will be same as for the Schwarzschild vacuum. Third, with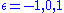
for timelike, null, spacelike geodesics, we find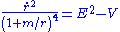
where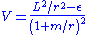
is a kind of effective potential. In the timelike case, we see from this that there exist stable circular orbits at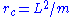
, which agrees perfectly with Newtonian theory (if we ignore the fact that now the angular but not the radial distance interpretation of r agrees with flat space notions). In contrast, in the Schwarzschild vacuum we have to first order in m the expression 
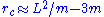. In a sense, the extra term here results from the nonlinearity of the vacuum Einstein field equation.
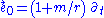
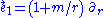
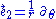
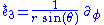
Then, the acceleration of the world line of our test particle is simply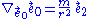
Thus, the particle must maintain radially outward to maintain its position, with a magnitude given by the familiar Newtonian expression (but again we must bear in mind that the radial coordinate here cannot quite be identified with a flat space radial coordinate). Put in other words, this is the "gravitational acceleration" measured by a static observer who uses a rocket engine to maintain his position. In contrast, to second order in m, in the Schwarzschild vacuum the magnitude of the radially outward acceleration of a static observer is m r-2 + m^2 r-3; here too, the second term expresses the fact that Einstein gravity is slightly stronger "at corresponding points" than Nordström gravity.
The tidal tensor measured by a static observer is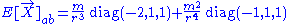
where we take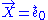
. The first term agrees with the corresponding solution in the Newtonian theory of gravitation and the one in general relativity. The second term shows that the tidal forces are a bit stronger in Nordström gravity than in Einstein gravity.
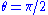we have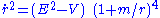
where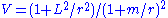
for a timelike geodesic. Differentiating with respect to proper time s, we obtain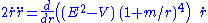
Dividing both sides by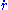
gives
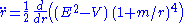
We found earlier that the minimum of V occurs at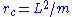
where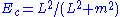 
. Evaluating the derivative, using our earlier results, and setting 
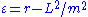, we find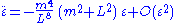
which is (to first order) the equation of simple harmonic motion
.
In other words, nearly circular orbits will exhibit a radial oscillation. However, unlike what happens in Newtonian gravitation, the period of this oscillation will not quite match the orbital period. This will result in slow precession of the periastria (points of closest approach) of our nearly circular orbit, or more vividly, in a slow rotation of the long axis of a quasi-Keplerian nearly elliptical orbit. Specifically,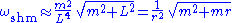
(where we used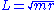
and removed the subscript from 
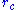), whereas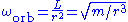
The discrepancy is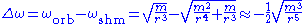
so the periastrion lag per orbit is
and to first order in m, the long axis of the nearly elliptical orbit rotates with the rate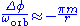
This can be compared with the corresponding expression for the Schwarzschild vacuum solution in general relativity, which is (to first order in m)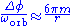
Thus, in Nordström's theory, if the nearly elliptical orbit is tranversed counterclockwise, the long axis slowly rotates clockwise, whereas in general relativity, it rotates counterclockwise six times faster. In the first case we may speak of a periastrion lag and in the second case, a periastrion advance. In either theory, with more work, we can derive more general expressions, but we shall be satisfied here with treating the special case of nearly circular orbits.
For example, according to Nordström's theory, the perihelia of Mercury
should lag at a rate of about 7 seconds of arc per century, whereas according to general relativity, the perihelia should advance at a rate of about 43 seconds of arc per century.
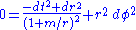
Consider two events on a null geodesic, before and after its point of closest approach to the origin.
Let these distances be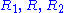
with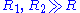 
. We wish to eliminate 
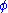, so put 
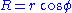(the equation of a straight line in polar coordinates) and differentiate to obtain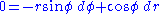
Thus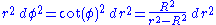
Plugging this into the line element and solving for dt, we obtain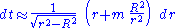
Thus the coordinate time from the first event to the event of closest approach is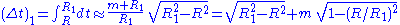
and likewise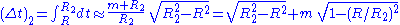
Here the elapsed coordinate time expected from Newtonian theory is of course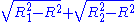
so the relativistic time delay, according to Nordström's theory, is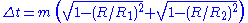
To first order in the small ratios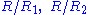
this is just 
.
The corresponding result in general relativity is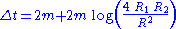
which depends logarithmically on the small ratios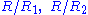
. For example, in the classic experiment in which, at a time when, as viewed from Earth
, Venus
is just about to pass behind the Sun
, a radar
signal emitted from Earth which grazes the limb of the Sun, bounces off Venus, and returns to Earth (once again grazing the limb of the Sun), the relativistic time delay is about is about 20 microsecond
s according to Nordström's theory and about 240 microseconds according to general relativity.
The last four lines in this table list the so-called four classic solar system tests of relativistic theories of gravitation. Of the three theories appearing in the table, only general relativity is in agreement with the results of experiments and observations in the solar system. Nordström's theory gives the correct result only for the Pound-Rebka experiment
; not surprisingly, Newton's theory flunks all four relativistic tests.
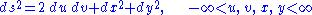
a simple solution of the wave equation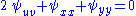
is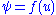
, where f is an arbitrary smooth function. This represents a plane wave
traveling in the z direction. Therefore, Nordström's theory admits the exact vacuum solution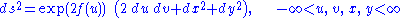
which we can interpret in terms of the propagation of a gravitational plane wave.
This Lorentzian manifold admits a six dimensional Lie group of isometries, or equivalently, a six dimensional Lie algebra of Killing vector fields: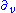
(a null translation, "opposing" the wave vector
field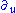
)
(spatial translation orthogonal to the wavefronts)
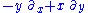(rotation about axis parallel to direction of propagation)
For example, the Killing vector field
integrates to give the one parameter family of isometries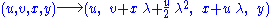
Just as in special relativity (and general relativity), it is always possible to change coordinates, without disturbing the form of the solution, so that the wave propagates in any direction transverse to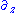
.
Note that our isometry group is transitive on the hypersurfaces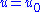
.
In contract, the generic gravitational plane wave
in general relativity has only a five dimensional Lie group of isometries. (In both theories, special plane waves may have extra symmetries.) We'll say a bit more about why this is so in a moment.
Adopting the frame field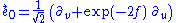
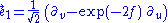
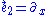
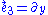
we find that the corresponding family of test particles are inertial (freely falling), since the acceleration vector
vanishes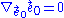
Notice that if f vanishes, this family becomes a family of mutually stationary test particles in flat (Minkowski) spacetime. With respect to the timelike geodesic congruence
of world line
s obtained by integrating the timelike unit vector field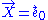
, the expansion tensor
shows that our test particles are expanding or contracting isotropically and transversely to the direction of propagation. This is exactly what we would expect for a transverse spin-0 wave; the behavior of analogous families of test particles which encounter a gravitational plane wave in general relativity is quite different, because these are spin-2 waves. This is due to the fact that Nordström's theory of gravitation is a scalar theory, whereas Einstein's theory of gravitation (general relativity) is a tensor theory. On the other hand, gravitational waves in both theories are transverse waves. Electromagnetic plane waves are of course also transverse. The tidal tensor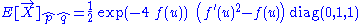
further exhibits the spin-0 character of the gravitational plane wave in Nordström's theory. (The tidal tensor and expansion tensor are three-dimensional tensors which "live" in the hyperplane elements orthogonal to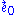
, which in this case happens to be irrotational, so we can regard these tensors as defined on orthogonal hyperslices.)
The exact solution we are discussing here, which we interpret as a propagating gravitational plane wave, gives some basic insight into the propagation of gravitational radiation in Nordström's theory, but it does not yield any insight into the generation of gravitational radiation in this theory. At this point, it would be natural to discuss the analog for Nordström's theory of gravitation of the standard linearized gravitational wave theory in general relativity, but we shall not pursue this.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, Nordström's theory of gravitation was a predecessor of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström
Gunnar Nordström
Gunnar Nordström was a Finnish theoretical physicist best remembered for his theory of gravitation, which was an early competitor of general relativity...
, in 1912 and 1913 respectively. The first was quickly dismissed, but the second became the first known example of a metric theory of gravitation
Classical theories of gravitation
The current Gold Standard Theory of Gravitation is the general theory of relativity. This is a classical, relativistic field theory of gravitation...
, in which the effects of gravitation are treated entirely in terms of the geometry of a curved spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
Neither of Nordström's theories are in agreement with observation and experiment. Nonetheless, the first remains of interest insofar as it led to the second. The second remains of interest both as an important milestone on the road to the current theory of gravitation, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, and as a simple example of a self-consistent relativistic theory of gravitation. As an example, this theory is particularly useful in the context of pedagogical discussions of how to derive and test the predictions of a metric theory of gravitation.
Development of the theories
Nordström's theories arose at a time when several leading physicists, including Nordström in HelsinkiHelsinki
Helsinki is the capital and largest city in Finland. It is in the region of Uusimaa, located in southern Finland, on the shore of the Gulf of Finland, an arm of the Baltic Sea. The population of the city of Helsinki is , making it by far the most populous municipality in Finland. Helsinki is...
, Max Abraham
Max Abraham
Max Abraham was a German physicist.Abraham was born in Danzig, Imperial Germany to a family of Jewish merchants. His father was Moritz Abraham and his mother was Selma Moritzsohn. Attending the University of Berlin, he studied under Max Planck. He graduated in 1897...
in Milan
Milan
Milan is the second-largest city in Italy and the capital city of the region of Lombardy and of the province of Milan. The city proper has a population of about 1.3 million, while its urban area, roughly coinciding with its administrative province and the bordering Province of Monza and Brianza ,...
, Gustav Mie
Gustav Mie
Gustav Adolf Feodor Wilhelm Ludwig Mie was a German physicist.-Biography:Mie was born in Rostock. From 1886 he studied mathematics and physics at the University of Rostock. In addition to his major subjects, he also attended lectures in chemistry, zoology, geology, mineralogy, astronomy as well as...
in Greifswald
Greifswald
Greifswald , officially, the University and Hanseatic City of Greifswald is a town in northeastern Germany. It is situated in the state of Mecklenburg-Vorpommern, at an equal distance of about from Germany's two largest cities, Berlin and Hamburg. The town borders the Baltic Sea, and is crossed...
, Germany, and Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in Prague
Prague
Prague is the capital and largest city of the Czech Republic. Situated in the north-west of the country on the Vltava river, the city is home to about 1.3 million people, while its metropolitan area is estimated to have a population of over 2.3 million...
, were all trying to create competing relativistic theories of gravitation.
All of these researchers began by trying to suitably modify the existing theory, the field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
version of Newton's theory of gravitation. In this theory, the field equation
Field equation
A field equation is an equation in a physical theory that describes how a fundamental force interacts with matter...
is the Poisson equation
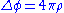, where 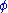is the gravitational potential and 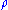is the density of matter, augmented by an equation of motion for a test particleTest particle
In physical theories, a test particle is an idealized model of an object whose physical properties are assumed to be negligible except for the property being studied, which is considered to be insufficient to alter the behavior of the rest of the system...
in an ambient gravitational field, which we can derive from
Newton's force law and which states that the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of the test particle is given by the gradient of the potential
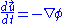
This theory is not relativistic because the equation of motion refers to coordinate time rather than proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
, and because, should the matter in some isolated object suddenly be redistributed by an explosion, the field equation requires that the potential everywhere in "space" must be "updated" instantaneously, which violates the principle that any "news" which has a physical effect (in this case, an effect on test particle
Test particle
In physical theories, a test particle is an idealized model of an object whose physical properties are assumed to be negligible except for the property being studied, which is considered to be insufficient to alter the behavior of the rest of the system...
motion far from the source of the field) cannot be transmitted faster than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. Einstein's former calculus professor, Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
had sketched a vector theory of gravitation as early as 1908, but in 1912, Abraham pointed out that no such theory would admit stable planetary orbits. This was one reason why Nordström turned to scalar theories of gravitation (while Einstein explored tensor theories).
Nordström's first attempt to propose a suitable relativistic scalar field equation of gravitation was the simplest and most natural choice imaginable: simply replace the Laplacian in the Newtonian field equation with the D'Alembertian or wave operator, which gives
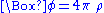. This has the result of changing the vacuum field equation from the Laplace equation to the wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, which means that any "news" concerning redistribution of matter in one location is transmitted at the speed of light to other locations. Correspondingly, the simplest guess for a suitable equation of motion for test particles might seem to be
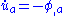where the dot signifies differentiation with respect to proper time and where 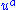is the velocity four-vector of the test particle. This force law had earlier been proposed by Abraham, and Nordström knew that it wouldn't work. Instead he proposed 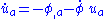.However, this theory is unacceptable for a variety of reasons. Two objections are theoretical. First, this theory is not derivable from a Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
, unlike the Newtonian field theory (or most metric theories of gravitation). Second, the proposed field equation is linear. But by analogy with electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, we should expect the gravitational field to carry energy, and on the basis of Einstein's work on relativity theory, we should expect this energy to be equivalent to mass and therefore, to gravitate. This implies that the field equation should be nonlinear. Another objection is more practical: this theory disagrees drastically with observation.
Einstein and von Laue proposed that the problem might lie with the field equation, which, they suggested, should have the linear form
, where F is some yet unknown function of 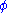, and where Tmatter is the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
describing the density, momentum, and stress of any matter present.
In response to these criticisms, Nordström proposed his second theory in 1913. From the proportionality of inertial and gravitational mass, he deduced that the field equation should be
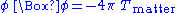, which is nonlinear. Nordström now took the equation of motion to be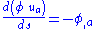or
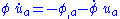.Einstein took the first opportunity to proclaim his approval of the new theory. In a keynote address to the annual meeting of the Society of German Scientists and Physicians, given in Vienna
Vienna
Vienna is the capital and largest city of the Republic of Austria and one of the nine states of Austria. Vienna is Austria's primary city, with a population of about 1.723 million , and is by far the largest city in Austria, as well as its cultural, economic, and political centre...
on September 23, 1913, Einstein surveyed the state of the art, declaring that only his own work with Marcel Grossmann
Marcel Grossmann
Marcel Grossmann was a mathematician of Jewish ancestry, and a friend and classmate of Albert Einstein. He became a Professor of Mathematics at the Federal Polytechnic Institute in Zurich, today the ETH Zurich, specializing in descriptive geometry....
and the second theory of Nordström were worthy of consideration. (Mie, who was in the audience, rose to protest, but Einstein explained his criteria and Mie was forced to admit that his own theory did not meet them.) Einstein considered the special case when the only matter present is a cloud of dust (that is, a perfect fluid
Perfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
in which the pressure is assumed to be negligible). He argued that the contribution of this matter to the stress-energy tensor should be:
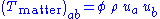
He then derived an expression for the stress-energy tensor of the gravitational field in Nordström's second theory,
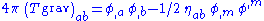
which he proposed should hold in general, and showed that the sum of the contributions to the stress-energy tensor from the gravitational field energy and from matter would be conserved, as should be the case. Furthermore, he showed, the field equation of Nordström's second theory follows from the Lagrangian
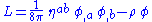
Since Nordström's equation of motion for test particles in an ambient gravitational field also follows from a Lagrangian, this shows that Nordström's second theory can be derived from an action principle and also shows that it obeys other properties we must demand from a self-consistent field theory.
Meanwhile, a gifted Dutch student, Adriaan Fokker
Adriaan Fokker
Adriaan Daniël Fokker , was a Dutch physicist and musician.Fokker was born in Buitenzorg, Dutch East Indies ; he was a cousin of the aeronautical engineer Anthony Fokker...
had written a Ph.D. thesis under Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
in which he derived what is now called the Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
. Lorentz, delighted by his former student's success, arranged for Fokker to pursue post-doctoral study with Einstein in Prague. The result was a historic paper which appeared in 1914, in which Einstein and Fokker observed that the Lagrangian for Nordström's equation of motion for test particles,
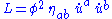, is the geodesic Lagrangian for a curved Lorentzian manifold with metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
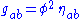. If we adopt Cartesian coordinates with line element 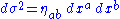with corresponding wave operator 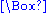on the flat background, or Minkowski spacetime, so that the line element of the curved spacetime is 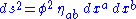, then the Ricci scalar of this curved spacetime is just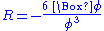Therefore Nordström's field equation becomes simply
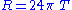
where on the right hand side, we have taken the trace of the stress-energy tensor (with contributions from matter plus any non-gravitational fields) using the metric tensor
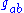. This is a historic result, because here for the first time we have a field equation in which on the left hand side stands a purely geometrical quantity (the Ricci scalar is the trace of the Ricci tensor, which is itself a kind of trace of the fourth rank Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
), and on the right hand stands a purely physical quantity, the trace of the stress-energy tensor. Einstein gleefully pointed out that this equation now takes the form which he had earlier proposed with von Laue, and gives a concrete example of a class of theories which he had studied with Grossmann.
Some time latter, Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
introduced the Weyl curvature tensor
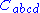, which measures the deviation of a Lorentzian manifold from being conformally flat, i.e. with metric tensor having the form of the product of some scalar function with the metric tensor of flat spacetime. This is exactly the special form of the metric proposed in Nordström's second theory, so the entire content of this theory can be even more elegantly summarized in the following two equations:Features of Nordström's theory
Einstein's enthusiasm for Nordström's second theory is well-grounded in some remarkably attractive features. Not only are the field equations strikingly simple and elegant, the vacuum field equations in Nordström's theory are simplyWe can immediately write down the general vacuum solution in Nordström's theory:
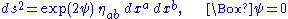
where
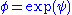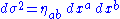and is the line element for flat spacetime in any convenient coordinate chart (such as cylindrical, polar spherical, or double null coordinates), and where is the ordinary wave operator on flat spacetime (expressed in cylindrical, polar spherical, or double null coordinates, respectively). But the general solution of the ordinary three dimensional wave equation is well known, and can be given rather explicit form. Specifically, for certain charts such as cylindrical or polar spherical charts on flat spacetime (which induce corresponding charts on our curved Lorentzian manifold), we can write the general solution in terms of a power series, and we can write the general solution of certain Cauchy problemCauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
s in the manner familiar from the Lienard-Wiechert potentials in electromagnetism.
In any solution to Nordström's field equations (vacuum or otherwise), if we consider
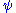as controlling a conformal perturbation from flat spacetime, then to first order in 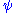we have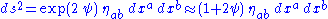Thus, in the weak field approximation, we can identify
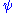with the Newtonian gravitational potential, and we can regard it as controlling a small conformal perturbation from a flat spacetime background.In any metric theory of gravitation, all gravitational effects arise from the curvature of the metric. In a spacetime model in Nordström's theory (but not in general relativity), this depends only on the trace of the stress-energy tensor. But the field energy of an electromagnetic field contributes a term to the stress-energy tensor which is traceless, so in Nordström's theory, electromagnetic field energy does not gravitate! Indeed, since every solution to the field equations of this theory is a spacetime which is among other things conformally equivalent to flat spacetime, null geodesics must agree with the null geodesics of the flat background, so this theory can exhibit no light bending.
Incidentally, the fact that the trace of the stress-energy tensor for an electrovacuum solution
Electrovacuum solution
In general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
(a solution in which there is no matter present, nor any non-gravitational fields except for an electromagnetic field) vanishes shows that in the general electrovacuum solution in Nordström's theory, the metric tensor has the same form as in a vacuum solution, so we need only write down and solve the curved spacetime Maxwell field equations
Maxwell's equations in curved spacetime
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system...
. But these are conformally invariant, so we can also write down the general electrovacuum solution, say in terms of a power series.
In any Lorentzian manifold (with appropriate tensor fields describing any matter and physical fields) which stands as a solution to Nordström's field equations, the conformal part of the Riemann tensor (i.e. the Weyl tensor) always vanishes. The Ricci scalar also vanishes identically in any vacuum region (or even, any region free of matter but containing an electromagnetic field). Are there any further restrictions on the Riemann tensor in Nordström's theory?
To find out, note that an important identity from the theory of manifolds, the Ricci decomposition
Ricci decomposition
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
, splits the Riemann tensor into three pieces, which are each fourth-rank tensors, built out of, respectively, the Ricci scalar, the trace-free Ricci tensor
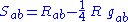
and the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
. It immediately follows that Nordström's theory leaves the trace-free Ricci tensor entirely unconstrained by algebraic relations (other than the symmetric property, which this second rank tensor always enjoys). But taking account of the twice-contracted and detraced Bianchi identity, a differential identity which holds for the Riemann tensor in any (semi)-Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, we see that in Nordström's theory, as a consequence of the field equations, we have the first-order covariant differential equation
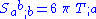
which constrains the semi-traceless part of the Riemann tensor (the one built out of the trace-free Ricci tensor).
Thus, according to Nordström's theory, in a vacuum region only the semi-traceless part of the Riemann tensor can be nonvanishing. Then our covariant differential constraint on
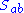shows how variations in the trace of the stress-energy tensor in our spacetime model can generate a nonzero trace-free Ricci tensor, and thus nonzero semi-traceless curvature, which can propagate into a vacuum region. This is critically important, because otherwise gravitation would not, according to this theory, be a long-range force capable of propagating through a vacuum.In general relativity, something somewhat analogous happens, but there it is the Ricci tensor which vanishes in any vacuum region (but not in a region which is matter-free but contains an electromagnetic field), and it is the Weyl curvature which is generated (via another first order covariant differential equation) by variations in the stress-energy tensor and which then propagates into vacuum regions, rendering gravitation a long-range force capable of propagating through a vacuum.
We can tabulate the most basic differences between Nordström's theory and general relativity, as follows:
| type of curvature | Nordström | Einstein | |
|---|---|---|---|
 |
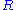scalar | vanishes in electrovacuum | vanishes in electrovacuum |
 |
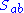once traceless | nonzero for gravitational radiation | vanishes in vacuum |
 |
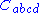completely traceless | vanishes always | nonzero for gravitational radiation |
Another very striking feature of Nordström's theory is that it while it can be written as the theory of a certain scalar field in Minkowski spacetime, and in this form enjoys the expected conservation law for nongravitational mass-energy together with gravitational field energy, but suffers from a not very memorable force law, in the curved spacetime formulation the motion of test particles is very elegantly described (the world line of a free test particle is a timelike geodesic, and by an obvious limit, the world line of a laser pulse is a null geodesic), but we lose the conservation law. So which interpretation is correct? In other words, which metric is the one which according to Nordström can be measured locally by physical experiments? The answer is: the curved spacetime is the physically observable one in this theory (as in all metric theories of gravitation); the flat background is a mere mathematical fiction which is however of inestimable value for such purposes as writing down the general vacuum solution, or studying the weak field limit.
At this point, we could show that in the limit of slowly moving test particles and slowly evolving weak gravitational fields, Nordström's theory of gravitation reduces to the Newtonian theory of gravitation. Rather than showing this in detail, we will proceed to a detailed study the two most important solutions in this theory:
- the spherically symmetric static asymptotically flat vacuum solutions
- the general vacuum gravitational plane wave solution in this theory.
We will use the first to obtain the predictions of Nordström's theory for the four classic solar system tests of relativistic gravitation theories (in the ambient field of an isolated spherically symmetric object), and we will use the second to compare gravitational radiation in Nordström's theory and in Einstein's general theory of relativity.
The static spherically symmetric asymptotically flat vacuum solution
The static vacuum solutions in Nordström's theory are the Lorentzian manifolds with metrics of the form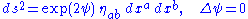where we can take the flat spacetime Laplace operator on the right. To first order in
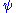, the metric becomes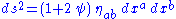where
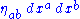is the metric of Minkowski spacetime (the flat background).The metric
Adopting polar spherical coordinates, and using the known spherically symmetric asymptotically vanishing solutions of the Laplace equation, we can write the desired exact solution as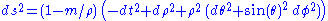where we justify our choice of integration constants by the fact that this is the unique choice giving the correct Newtonian limit. This gives the solution in terms of coordinates which directly exhibit the fact that this spacetime is conformally equivalent to Minkowski spacetime, but the radial coordinate in this chart does not readily admit a direct geometric interpretation. Therefore, we adopt instead Schwarzschild coordinates, using the transformation
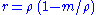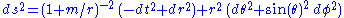
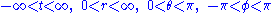
, which brings the metric into the formHere, r now has the simple geometric interpretation that the surface area of the coordinate sphere
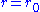is just 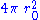.Just as happens in the corresponding static spherically symmetric asymptotically flat solution of general relativity, this solution admits a four dimensional Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of isometries, or equivalently, a four dimensional (real) Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of Killing vector fields. These are readily determined to be
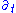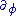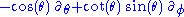
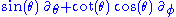
(translation in time) (rotation about an axis through the origin)These are exactly the same vector fields which arise in the Schwarzschild coordinate chart for the Schwarzschild vacuum solution
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
of general relativity, and they simply express the fact that this spacetime is static and spherically symmetric.
Geodesics
The geodesic equations are readily obtained from the geodesic Lagrangian. As always, these are second order nonlinear ordinary differential equations.If we set
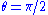we find that test particle motion confined to the equatorial plane is possible, and in this case first integrals (first order ordinary differential equations) are readily obtained. First, we have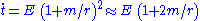where to first order in m we have the same result as for the Schwarzschild vacuum. This also shows that Nordström's theory agrees with the result of the Pound-Rebka experiment
Pound-Rebka experiment
The Pound–Rebka experiment is a well known experiment to test Albert Einstein's theory of general relativity. It was proposed by Robert Pound and his graduate student Glen A. Rebka Jr. in 1959, and was the last of the classical tests of general relativity to be verified...
. Second, we have
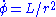
which is the same result as for the Schwarzschild vacuum. This expresses conservation of orbital anglar momentum of test particles moving in the equatorial plane, and shows that the period of a nearly circular orbit (as observed by a distant observer) will be same as for the Schwarzschild vacuum. Third, with
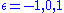for timelike, null, spacelike geodesics, we find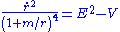where
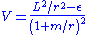
is a kind of effective potential. In the timelike case, we see from this that there exist stable circular orbits at
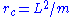, which agrees perfectly with Newtonian theory (if we ignore the fact that now the angular but not the radial distance interpretation of r agrees with flat space notions). In contrast, in the Schwarzschild vacuum we have to first order in m the expression 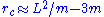. In a sense, the extra term here results from the nonlinearity of the vacuum Einstein field equation.Static observers
It makes sense to ask how much force is required to hold a test particle with a given mass over the massive object which we assume is the source of this static spherically symmetric gravitational field. To find out, we need only adopt the simple frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
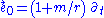
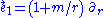
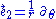
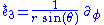
Then, the acceleration of the world line of our test particle is simply
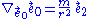
Thus, the particle must maintain radially outward to maintain its position, with a magnitude given by the familiar Newtonian expression (but again we must bear in mind that the radial coordinate here cannot quite be identified with a flat space radial coordinate). Put in other words, this is the "gravitational acceleration" measured by a static observer who uses a rocket engine to maintain his position. In contrast, to second order in m, in the Schwarzschild vacuum the magnitude of the radially outward acceleration of a static observer is m r-2 + m^2 r-3; here too, the second term expresses the fact that Einstein gravity is slightly stronger "at corresponding points" than Nordström gravity.
The tidal tensor measured by a static observer is
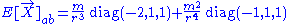
where we take
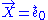. The first term agrees with the corresponding solution in the Newtonian theory of gravitation and the one in general relativity. The second term shows that the tidal forces are a bit stronger in Nordström gravity than in Einstein gravity.Extra-Newtonian precession of periastria
In our discussion of the geodesic equations, we showed that in the equatorial coordinate plane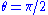 we have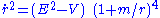where
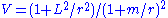for a timelike geodesic. Differentiating with respect to proper time s, we obtain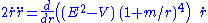Dividing both sides by
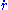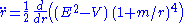
givesWe found earlier that the minimum of V occurs at
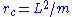where 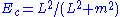. Evaluating the derivative, using our earlier results, and setting 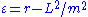, we find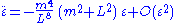which is (to first order) the equation of simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
.
In other words, nearly circular orbits will exhibit a radial oscillation. However, unlike what happens in Newtonian gravitation, the period of this oscillation will not quite match the orbital period. This will result in slow precession of the periastria (points of closest approach) of our nearly circular orbit, or more vividly, in a slow rotation of the long axis of a quasi-Keplerian nearly elliptical orbit. Specifically,
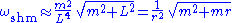
(where we used
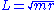and removed the subscript from 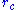), whereas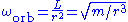The discrepancy is
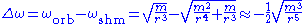
so the periastrion lag per orbit is
and to first order in m, the long axis of the nearly elliptical orbit rotates with the rate
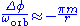
This can be compared with the corresponding expression for the Schwarzschild vacuum solution in general relativity, which is (to first order in m)
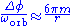
Thus, in Nordström's theory, if the nearly elliptical orbit is tranversed counterclockwise, the long axis slowly rotates clockwise, whereas in general relativity, it rotates counterclockwise six times faster. In the first case we may speak of a periastrion lag and in the second case, a periastrion advance. In either theory, with more work, we can derive more general expressions, but we shall be satisfied here with treating the special case of nearly circular orbits.
For example, according to Nordström's theory, the perihelia of Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
should lag at a rate of about 7 seconds of arc per century, whereas according to general relativity, the perihelia should advance at a rate of about 43 seconds of arc per century.
Light delay
Null geodesics in the equatorial plane of our solution satisfy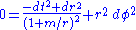Consider two events on a null geodesic, before and after its point of closest approach to the origin.
Let these distances be
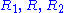with 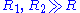. We wish to eliminate 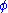, so put 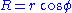(the equation of a straight line in polar coordinates) and differentiate to obtain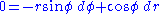Thus
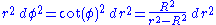
Plugging this into the line element and solving for dt, we obtain
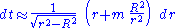
Thus the coordinate time from the first event to the event of closest approach is
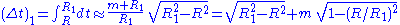
and likewise
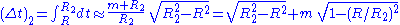
Here the elapsed coordinate time expected from Newtonian theory is of course
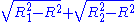
so the relativistic time delay, according to Nordström's theory, is
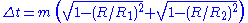
To first order in the small ratios
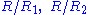this is just .The corresponding result in general relativity is
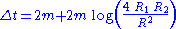
which depends logarithmically on the small ratios
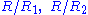. For example, in the classic experiment in which, at a time when, as viewed from EarthEarth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
is just about to pass behind the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, a radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
signal emitted from Earth which grazes the limb of the Sun, bounces off Venus, and returns to Earth (once again grazing the limb of the Sun), the relativistic time delay is about is about 20 microsecond
Microsecond
A microsecond is an SI unit of time equal to one millionth of a second. Its symbol is µs.A microsecond is equal to 1000 nanoseconds or 1/1000 millisecond...
s according to Nordström's theory and about 240 microseconds according to general relativity.
Summary of results
We can summarize the results we found above in the following table, in which the given expressions represent appropriate approximations:| Newton | Nordström | Einstein | |
|---|---|---|---|
| Acceleration of static test particle | m r-2 | m r-2 | m r-2 + m2 r-3 |
| Extra-Coulomb tidal force | 0 | m2 r-4 diag(-1,1,1) | 0 |
| Radius of circular orbit | R = L2 m -1 | R = L2 m -1 | R = L2 m-1 - 3 m |
| Gravitational red shift factor | 1 | 1 + m r -1 | 1 + m r -1 |
| Angle of light bending |  |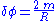
0 |  |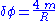
| Rate of precession of periastria | 0 |  |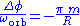
 |
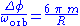| Time delay | 0 |  |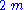
 |
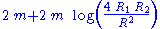The last four lines in this table list the so-called four classic solar system tests of relativistic theories of gravitation. Of the three theories appearing in the table, only general relativity is in agreement with the results of experiments and observations in the solar system. Nordström's theory gives the correct result only for the Pound-Rebka experiment
Pound-Rebka experiment
The Pound–Rebka experiment is a well known experiment to test Albert Einstein's theory of general relativity. It was proposed by Robert Pound and his graduate student Glen A. Rebka Jr. in 1959, and was the last of the classical tests of general relativity to be verified...
; not surprisingly, Newton's theory flunks all four relativistic tests.
Vacuum gravitational plane wave
In the double null chart for Minkowski spacetime,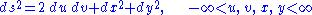a simple solution of the wave equation
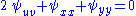
is
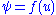, where f is an arbitrary smooth function. This represents a plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
traveling in the z direction. Therefore, Nordström's theory admits the exact vacuum solution
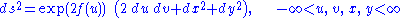
which we can interpret in terms of the propagation of a gravitational plane wave.
This Lorentzian manifold admits a six dimensional Lie group of isometries, or equivalently, a six dimensional Lie algebra of Killing vector fields:
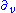(a null translation, "opposing" the wave vectorWave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
field
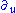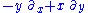) (spatial translation orthogonal to the wavefronts) (rotation about axis parallel to direction of propagation)For example, the Killing vector field
integrates to give the one parameter family of isometries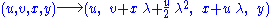Just as in special relativity (and general relativity), it is always possible to change coordinates, without disturbing the form of the solution, so that the wave propagates in any direction transverse to
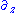.Note that our isometry group is transitive on the hypersurfaces
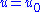.In contract, the generic gravitational plane wave
Gravitational plane wave
In general relativity, a gravitational plane wave is a special class of a vacuum pp-wave spacetime, and may be defined in terms of Brinkmann coordinates byds^2=[a+2bxy]du^2+2dudv+dx^2+dy^2...
in general relativity has only a five dimensional Lie group of isometries. (In both theories, special plane waves may have extra symmetries.) We'll say a bit more about why this is so in a moment.
Adopting the frame field
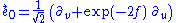
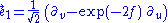
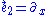
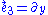
we find that the corresponding family of test particles are inertial (freely falling), since the acceleration vector
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
vanishes
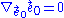
Notice that if f vanishes, this family becomes a family of mutually stationary test particles in flat (Minkowski) spacetime. With respect to the timelike geodesic congruence
Congruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
of world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s obtained by integrating the timelike unit vector field
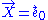, the expansion tensorshows that our test particles are expanding or contracting isotropically and transversely to the direction of propagation. This is exactly what we would expect for a transverse spin-0 wave; the behavior of analogous families of test particles which encounter a gravitational plane wave in general relativity is quite different, because these are spin-2 waves. This is due to the fact that Nordström's theory of gravitation is a scalar theory, whereas Einstein's theory of gravitation (general relativity) is a tensor theory. On the other hand, gravitational waves in both theories are transverse waves. Electromagnetic plane waves are of course also transverse. The tidal tensor
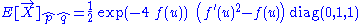
further exhibits the spin-0 character of the gravitational plane wave in Nordström's theory. (The tidal tensor and expansion tensor are three-dimensional tensors which "live" in the hyperplane elements orthogonal to
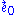, which in this case happens to be irrotational, so we can regard these tensors as defined on orthogonal hyperslices.)The exact solution we are discussing here, which we interpret as a propagating gravitational plane wave, gives some basic insight into the propagation of gravitational radiation in Nordström's theory, but it does not yield any insight into the generation of gravitational radiation in this theory. At this point, it would be natural to discuss the analog for Nordström's theory of gravitation of the standard linearized gravitational wave theory in general relativity, but we shall not pursue this.
See also
- Classical theories of gravitationClassical theories of gravitationThe current Gold Standard Theory of Gravitation is the general theory of relativity. This is a classical, relativistic field theory of gravitation...
- Congruence (general relativity)Congruence (general relativity)In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
- Gunnar NordströmGunnar NordströmGunnar Nordström was a Finnish theoretical physicist best remembered for his theory of gravitation, which was an early competitor of general relativity...
- Obsolete physical theories
- General Theory of Relativity