
Operad theory
Encyclopedia
Operad theory is a field of abstract algebra
concerned with prototypical algebras that model properties such as commutativity
or anticommutativity
as well as various amounts of associativity
. Operads generalize the various associativity
properties already observed in algebras
and coalgebra
s such as Lie algebra
s or Poisson algebra
s by modeling computational trees within the algebra. Algebras are to operads as group representations are to groups. Originating from work in algebraic topology by Boardman and Vogt, and J. Peter May
(to whom their name is due), it has more recently found many applications, drawing for example on work by Maxim Kontsevich
on graph homology.
An operad can be seen as a set of operations
, each one having a fixed finite number of inputs (arguments) and one output, which can be composed one with others; it is a category-theoretic analog of universal algebra
.
, an operad without permutations (sometimes called a non-symmetric, non- or plain operad) is a multicategory with one object. More explicitly, such an operad consists of the following:
or plain operad) is a multicategory with one object. More explicitly, such an operad consists of the following:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
concerned with prototypical algebras that model properties such as commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
or anticommutativity
Anticommutativity
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
as well as various amounts of associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
. Operads generalize the various associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
properties already observed in algebras
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
and coalgebra
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
s such as Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s or Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
s by modeling computational trees within the algebra. Algebras are to operads as group representations are to groups. Originating from work in algebraic topology by Boardman and Vogt, and J. Peter May
J. Peter May
Jon Peter May is an American mathematician, working in the fields of algebraic topology, category theory, homotopy theory, and the foundational aspects of spectra. He is known, in particular, for inventing the term operads and the May spectral sequence.He received a B.A. from Swarthmore College in...
(to whom their name is due), it has more recently found many applications, drawing for example on work by Maxim Kontsevich
Maxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
on graph homology.
An operad can be seen as a set of operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
, each one having a fixed finite number of inputs (arguments) and one output, which can be composed one with others; it is a category-theoretic analog of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
.
Definition
In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, an operad without permutations (sometimes called a non-symmetric, non-
 or plain operad) is a multicategory with one object. More explicitly, such an operad consists of the following:
or plain operad) is a multicategory with one object. More explicitly, such an operad consists of the following:
- a sequence
 of sets, whose elements are called
of sets, whose elements are called  -ary operations,
-ary operations, - for each positive integers
 ,
,  , ...,
, ..., 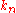 a function
a function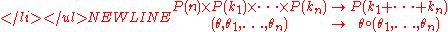
- called composition,
- an element
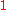 in
in  called the identity,
called the identity,
- an element
satisfying the following coherence properties:- associativity:
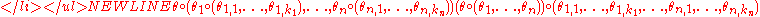
- identity:
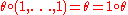
(where the number of arguments correspond to the arities of the operations).
A morphism of operads consists of a sequence
consists of a sequence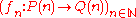
which:- preserves composition: for every n-ary operation
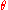 and operations
and operations 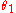 , ...,
, ...,  ,
,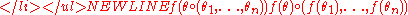
- preserves identity:
 .
.
Operads were originally defined topologically, by May, but his full definition requires symmetric
group actions on the that are suitably related to the maps
that are suitably related to the maps 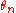 . The permutation actions
. The permutation actions
are additional structure that is vital to the original and most later applications.
Axiom of associativity
"Associativity" means that composition of operations is associative
(the function is associative), analogous to the axiom in category theory that
is associative), analogous to the axiom in category theory that 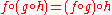 ; it does not mean that the operations themselves are associative as operations.
; it does not mean that the operations themselves are associative as operations.
Compare with the associative operad, below.
Associativity in operad theory means that one can write expressionsExpression (mathematics)In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
involving operations without ambiguity from the omitted compositions, just as associativity for operations allows one to write products without ambiguity from the omitted parentheses.
For instance, suppose that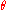 is a binary operation, which is written as
is a binary operation, which is written as 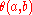 or
or  . Note that
. Note that 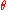 may or may not be associative.
may or may not be associative.
Then what is commonly written is unambiguously written operadically as
is unambiguously written operadically as 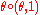 :
:
 sends
sends  to
to 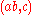 (apply
(apply 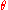 on the first two, and the identity on the third), and then the
on the first two, and the identity on the third), and then the  on the left "multiplies"
on the left "multiplies"  by
by  .
.
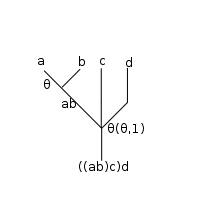
This is clearer when depicted as a tree:
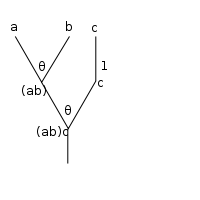
which yields a 3-ary operation:
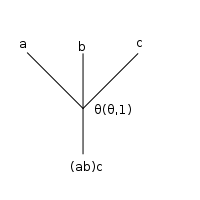
However, the expression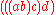 is a priori ambiguous:
is a priori ambiguous:
it could mean , if the inner compositions are performed first, or it could mean
, if the inner compositions are performed first, or it could mean  ,
,
if the outer compositions are performed first (operations are read from right to left).
Writing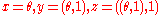 , this is
, this is 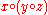 versus
versus 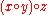 . That is, the tree is missing "vertical parentheses":
. That is, the tree is missing "vertical parentheses":
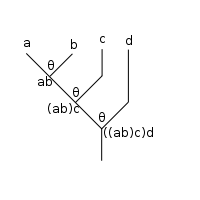
If the top two rows of operations are composed first (puts an upward parenthesis at the line; does the inner composition first), the following results:
line; does the inner composition first), the following results:
which then evaluates unambiguously to yield a 4-ary operation.
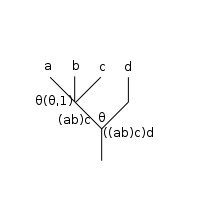
As an annotated expression:
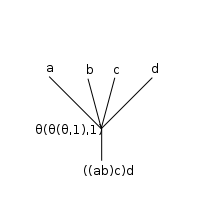
If the bottom two rows of operations are composed first (puts a downward parenthesis at the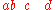 line; does the outer composition first), following results:
line; does the outer composition first), following results:
which then evaluates unambiguously to yield a 4-ary operation:

The operad axiom of associativity is that these yield the same result, and thus that the expression is unambiguous.
is unambiguous.
Axiom of identity
The axiom of identity (for a binary operation) can be visualized in a tree as:
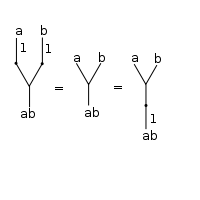
meaning that the three operations obtained are equal: pre- or post- composing with the identity makes no difference.
Note that, as for categories, is a corollary of the axiom of identity.
is a corollary of the axiom of identity.
Examples
 One class of examples of operads are those capturing the structures of algebraic structures, such as associative algebras, commutative algebras and Lie algebras. Each of these can be exhibited as a finitely presented operad, in each of these three generated by binary operations.
One class of examples of operads are those capturing the structures of algebraic structures, such as associative algebras, commutative algebras and Lie algebras. Each of these can be exhibited as a finitely presented operad, in each of these three generated by binary operations.
"Little something" operads
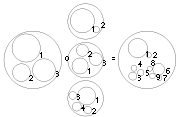
A little discs operad or, little balls operad or, more specifically, the little n-discs operad is a topological operad defined in terms of configurations of disjoint n-dimensional discs inside a unit n-disc centered in the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of Rn. The operadic composition for little 2-discs is illustrated in the figure.
Originally the little n-cubes operad or the little intervals operad (initially called little n-cubes PROPs) was defined by Michael BoardmanMichael BoardmanJohn Michael Boardman is a mathematician whose speciality is algebraic and differential topology. He was formerly at the University of Cambridge, England; he is currently a full professor at Johns Hopkins University in Baltimore, Maryland USA...
and Rainer Vogt in a similar way, in terms of configurations of disjoint axis-aligned n-dimensional hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s (n-dimensional intervalIntervalInterval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
s) inside the unit hypercube. Later it was generalized by May to little convex bodies operad, and "little discs" is a case of "folklore" derived from the "little convex bodies".
Associative operad
Thus, the associative operad is generated by a binary operation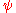 , subject to the condition that
, subject to the condition that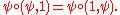
This condition does correspond to associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of the binary operation ; writing
; writing 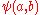 multiplicatively, the above condition is
multiplicatively, the above condition is  . This associativity of the operation should not be confused with associativity of composition; see the axiom of associativity, above.
. This associativity of the operation should not be confused with associativity of composition; see the axiom of associativity, above.
This operad is terminal in the category of non-symmetric operads, as it has exactly one n-ary operation for each n, corresponding to the unambiguous product of n terms: . For this reason, it is sometimes written as 1 by category theorists (by analogy with the one-point set, which is terminal in the category of sets).
. For this reason, it is sometimes written as 1 by category theorists (by analogy with the one-point set, which is terminal in the category of sets).
Terminal symmetric operad
The terminal symmetric operad is the operad whose algebras are commutative monoids, which also has one n-ary operation for each n, with each acting trivially; this triviality corresponds to commutativity, and whose n-ary operation is the unambiguous product of n-terms, where order does not matter:
acting trivially; this triviality corresponds to commutativity, and whose n-ary operation is the unambiguous product of n-terms, where order does not matter: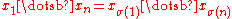
for any permutation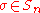 .
.
Operads in topology
In many examples the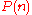 are not just sets but rather topological spaces. Some names of important
are not just sets but rather topological spaces. Some names of important
examples are the little n-disks, little n-cubes, and linear isometries operads. The idea behind the
little n-disks operad comes from homotopy theory, and the idea is that an element of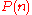
is an arrangement of n disks within the unit disk. Now, the identity is the unit disk as a subdisk of itself, and composition of arrangements is by scaling the unit disk down into the disk that corresponds to the slot in the composition, and inserting the scaled contents there.
Operads from the symmetric and braid groups
There is an operad for which each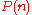 is given by the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
is given by the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
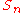 . The composite
. The composite  permutes its inputs in blocks according to
permutes its inputs in blocks according to  , and within blocks according to the appropriate
, and within blocks according to the appropriate  . Similarly, there is an operad for which each
. Similarly, there is an operad for which each 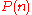 is given by the Artin braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
is given by the Artin braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
 .
.
Linear algebra
In linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, one can consider vector spaces to be algebras over the operad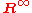 (the infinite direct sumDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
(the infinite direct sumDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
, so only finitely many terms are non-zero; this corresponds to only taking finite sums), which parametrizes linear combinations: the vector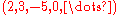 for instance corresponds to the linear combination
for instance corresponds to the linear combination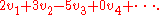
Similarly, one can consider affine combinations, conical combinationConical combinationGiven a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
s, and convex combinationConvex combinationIn convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by being or the standard simplex being model spaces, and such observations as that every bounded convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
being or the standard simplex being model spaces, and such observations as that every bounded convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
is the image of a simplex. Here suboperads correspond to more restricted operations and thus more general theories.
This point of view formalizes the notion that linear combinations are the most general sort of operation on a vector space – saying that a vector space is an algebra over the operad of linear combinations is precisely the statement that all possible algebraic operations in a vector space are linear combinations. The basic operations of vector addition and scalar multiplication are a generating setGenerating setIn mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
for the operad of all linear combinations, while the linear combinations operad canonically encode all possible operations on a vector space.
Origins of the term
The word "operad" was also created by May as a portmanteau of "operations" and "monadMonad (category theory)In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
" (and also because his mother was an opera singer). Regarding its creation, he wrote: "The name 'operad' is a word that I coined myself, spending a week thinking of nothing else." (http://www.math.uchicago.edu/~may/PAPERS/mayi.pdf Page 2) - preserves identity:
- identity:
- called composition,

