In quantum optics

Quantum optics

Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...

, an optical phase space is a phase space

Phase space

In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...

 in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an optical system. For any such system, a plot of the quadratures against each other, possibly as functions of time, is called a phase diagram

Phase diagram

A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...

. If the quadratures are functions of time then the optical phase diagram can show the evolution of a quantum optical system with time.

An optical phase diagram can give insight into the properties and behaviors of the system that might otherwise not be obvious. This can allude to qualities of the system that can be of interest to an individual studying an optical system that would be very hard to deduce otherwise. Another use for an optical phase diagram is that it shows the evolution of the state of an optical system. This can be used to determine the state of the optical system at any point in time.

For convenience the reduced Planck constant is set equal to one and is just a rescaling of the results found throughout this article. That is, .

Background information

When developing a quantum theory of light it is very common to use an electromagnetic oscillator as a model.. An electromagnetic oscillator is an oscillation of the electric field due to an excitation of the electric field. Since the magnetic field is proportional to the rate of change of the electric field, this too oscillates. This gives rise to such phenomena as light and these are the systems being studied when looking at an optical phase space. These systems obey and evolve according to Maxwell's Equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

.

Let u(x,t) be a vector function describing a single mode of an electromagnetic oscillator. For simplicitity, it is assumed that this electromagnetic oscillator is contained in a vacuum. One such example is given by


where u₀ is the polarization vector, k is the wave vector

Wave vector

In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...

, w the frequency, and AB denotes the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

 between the vectors A and B. This is the equation for a plane wave

Plane wave

In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....

 and is a simple example of such an electromagnetic oscillator. The oscillators being examined could either be free waves in space or some normal mode contained in some cavity

Cavity

A cavity is a hole. It may refer to:*Dental cavity, damage to the structure of teeth*Body cavity, a fluid filled space in many animals where organs typically develop*Cavity wall, a wall consisting of two skins with a cavity....

.

A single mode of the electromagnetic oscillator is isolated from the rest of the system and examined. Such an oscillator can be described by the annihilation operator as the Hamiltonian is strictly a function of the 'annihilation operator' which is in turn responsible for the time evolution of the system. This can be interpreted as the quantized amplitude with which u can be excited. It can then be shown that the electric field strength (i.e. the electromagnetic oscillator used to model the system) is given by:


(where x_i is a single component of x, position). The Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

 for an electromagnetic oscillator is found by quantizing

Quantization (physics)

In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...

 the electromagnetic field

Electromagnetic field

An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...

 for this oscillator and the formula is given by:


(where w is the frequency of the spatial-temporal mode). The annihilation operator is the bosonic annihilation operator and so it obeys the commutation relation given by:


(which is shown in the article Creation and annihilation operators

Creation and annihilation operators

Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...

). The eigenstates of the annihilation operator are called coherent states:


It is important to note that the annihilation operator is not Hermitian

Hermitian

A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...

, therefore its eigenvalues can be complex, an important consequence.

Finally, the photon number is given by the operator which gives the number of photons in the given spatial-temporal mode, u.

Quadratures

Operators given by


and


are called the quadratures and they represent the real

Real

Real may also refer to:* Reality, the state of things as they actually exist, rather than as they may appear or may be thought to be.-Finance:* Inflation adjusted amountsCurrencies:* Brazilian realFormer currencies:* Mexican real* Portuguese real...

 and imaginary

Imaginary

Imaginary can refer to:* Imaginary , a concept in sociology* Imaginary number, a concept in mathematics* Imaginary time, a concept in physics* Imagination, a mental faculty* Object of the mind, an object of the imagination* Imaginary friend...

 parts of the complex amplitude represented by . The commutation relation between the two quadratures can easily be calculated: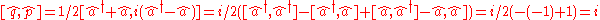


This looks very similar to the commutation relation of the position and momentum operator. Thus, it can be useful to think of and treat the quadratures as the position and momentum of the oscillator although in actual fact they are the "in-phase and out-of-phase components of the electric field amplitude of the spatial-temporal mode", or u, and have nothing really to do with the position or momentum of the electromagnetic oscillator (as it is hard to define what is meant by position and momentum for an electromagnetic oscillator).

Properties of quadratures

The eigenstates of the quadrature operators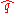 and 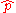are called the quadrature states. They satisfy the relations:

• and

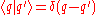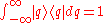• and

• and

as these form complete basis sets.

Important result

The following is an important relation that can be derived from the above which justifies our interpretation that the quadratures are the real and imaginary parts of a complex (i.e. the in-phase and out-of-phase components of the electromagnetic oscillator)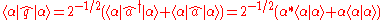


The following is a relationship that can be used to help evaluate the above and is given by:


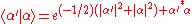
This gives us that:

by a similar method as above.


Thus, is just a composition of the quadratures.

Another very important property of the coherent states becomes very apparent in this formalism. A coherent state is not a point in the optical phase space but rather a distribution on it. This can be seen via


and
.

These are only the expected values of and for the state .

It can be shown that the quadratures obey Heisenberg's Uncertainty Principle given by:
(where and are the variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

s of the distributions of q and p, respectively)

This inequality does not necessarily have to be saturated and a common example of such states are squeezed coherent states. The coherent states are Gaussian probability distributions over the phase space localized around .

Operators on phase space

It is possible to define operators to move the coherent states around the phase space. These can produce new coherent states and allow us to move around phase space.

Phase-shifting operator

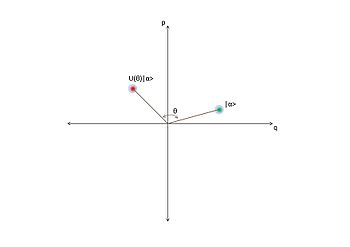
The phase-shifting operator rotates the coherent state by an angle in the optical phase space. This operator is given by: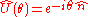


The important relationship


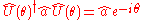
is derived as follows:



and solving this differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

 yields the desired result.

Thus, using the above it becomes clear that
,

or a rotation by an angle theta on the coherent state in phase space. The following illustrates this more clearly:


(which is obtained using the fact that the phase-shifting operator is unitary

Unitary

Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...

)


Thus,


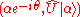
is the eigenpair

Eigenvalue, eigenvector and eigenspace

The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...

 of
.

From this it is possible to see that


which is another way of expressing the eigenpair which more clearly illustrates the effects of the phase-shifting operator on coherent states.

Displacement operator

The displacement operator takes a coherent state and moves it (by some value) to another coherent state somewhere in the phase space. The displacement operator is given by:


The relationship
.

can be derived quite easily.

To do this, take an infinitesimal displacement .

The operators and can be expanded in terms of the identity


and look at the first order terms and ignore all the higher order terms (all higher order terms are very close to zero as is very small).

Thus:

(but as given above, the higher order terms are very close to zero and therefore neglected)

(use the identity from above)


The above identity can be applied repeatedly in the following fashion to derive the following:


Thus, the above identity suggests that repeated use of the displacement operator generates translations in phase space.

Important consequence

The following is an important consequence of the displacement vector.

First note that the displacement operator is a unitary operator

Unitary operator

In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...

. Use


to get:




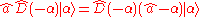
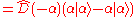
Thus,


or it follows that


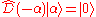
which leads to
.

This is important as it suggests that all coherent states are just displacements of the ground state

Ground state

The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...

, which in optics is also the vacuum state

Vacuum state

In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...

. That is, any coherent state can be generated via the displacement of the ground state of the electromagnetic oscillator from above.

See also

• Nonclassical light
  Nonclassical light
  Nonclassical light is any state of light that cannot be described using classical electromagnetism; its characteristics are described by the quantised electromagnetic field and quantum mechanics...
  
  
• Rotation operator (quantum mechanics)
• Quantum harmonic oscillator
  Quantum harmonic oscillator
  The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
  
  
• Quasi-probability distribution
• Husimi Q representation
  Husimi Q representation
  The Husimi-Q distribution is a mathematical tool used in physics, and was introduced in 1940. The Q-representation is a quasi-probability distribution commonly used in quantum mechanics and also to represent the quantum state of light. It is used in the field of quantum optics and particularly...
  
  
• Squeezed coherent state
• Wigner function