Ornstein–Uhlenbeck operator
Encyclopedia
In mathematics
, the Ornstein–Uhlenbeck operator can be thought of as a generalization of the Laplace operator
to an infinite-dimensional setting. The Ornstein–Uhlenbeck operator plays a significant role in the Malliavin calculus
.
operator ∇ acting on scalar functions f : Rn → R; the gradient of a scalar function is a vector field
v = ∇f : Rn → Rn. The divergence
operator div, acting on vector fields to produce scalar fields, is the adjoint operator to ∇. The Laplace operator Δ is then the composition
of the divergence and gradient operators:
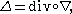
acting on scalar functions to produce scalar functions. Note that A = −Δ is a positive operator, whereas Δ is a dissipative operator.
Using spectral theory
, one can define a square root
(1 − Δ)1/2 for the operator (1 − Δ). This square root satisfies the following relation involving the Sobolev H1-norm
and L2-norm
for suitable scalar functions f:
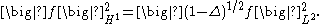
, which has many nice properties. However, remember that the aim is to work in infinite-dimensional spaces, and it is a fact that there is no infinite-dimensional Lebesgue measure
. Instead, if one is studying some separable Banach space
E, what does make sense is a notion of Gaussian measure
; in particular, the abstract Wiener space
construction makes sense.
To get some intuition about what can be expected in the infinite-dimensional setting, consider standard Gaussian measure γn on Rn: for Borel subsets A of Rn,
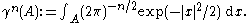
This makes (Rn, B(Rn), γn) into a probability space
; E will denoted expectation
with respect to γn.
The gradient operator ∇ acts on a (differentiable) function φ : Rn → R to give a vector field
∇φ : Rn → Rn.
The divergence operator δ (to be more precise, δn, since it depends on the dimension) is now defined to be the adjoint of ∇ in the Hilbert space
sense, in the Hilbert space L2(Rn, B(Rn), γn; R). In other words, δ acts on a vector field v : Rn → Rn to give a scalar function δv : Rn → R, and satisfies the formula
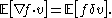
On the left, the product is the pointwise Euclidean dot product
of two vector fields; on the right, it is just the pointwise multiplication of two functions. Using integration by parts
, one can check that δ acts on a vector field v with components vi, i = 1, ..., n, as follows:
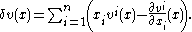
The change of notation from “div” to “δ” is for two reasons: first, δ is the notation used in infinite dimensions (the Malliavin calculus); secondly, δ is really the negative of the usual divergence.
The (finite-dimensional) Ornstein–Uhlenbeck operator L (or, to be more precise, Lm) is defined by
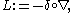
with the useful formula that for any f and g smooth enough for all the terms to make sense,
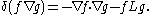
The Ornstein–Uhlenbeck operator L is related to the usual Laplacian Δ by
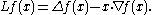
E with Cameron-Martin Hilbert space H and Wiener measure γ. Let D denote the Malliavin derivative
. The Malliavin derivative D is an unbounded operator
from L2(E, γ; R) into L2(E, γ; H) – in some sense, it measures “how random” a function on E is. The domain of D is not the whole of L2(E, γ; R), but is a dense
linear subspace
, the Watanabe-Sobolev space, often denoted by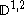
(once differentiable in the sense of Malliavin, with derivative in L2).
Again, δ is defined to be the adjoint of the gradient operator (in this case, the Malliavin derivative is playing the role of the gradient operator). The operator δ is also known the Skorokhod integral
, which is an anticipating stochastic integral; it is this set-up that gives rise to the slogan “stochastic integrals are divergences”. δ satisfies the identity
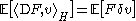
for all F in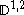
and u in the domain of δ.
Then the Ornstein–Uhlenbeck operator for E is the operator L defined by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Ornstein–Uhlenbeck operator can be thought of as a generalization of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
to an infinite-dimensional setting. The Ornstein–Uhlenbeck operator plays a significant role in the Malliavin calculus
Malliavin calculus
The Malliavin calculus, named after Paul Malliavin, is a theory of variational stochastic calculus. In other words it provides the mechanics to compute derivatives of random variables....
.
The Laplacian
Consider the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator ∇ acting on scalar functions f : Rn → R; the gradient of a scalar function is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
v = ∇f : Rn → Rn. The divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator div, acting on vector fields to produce scalar fields, is the adjoint operator to ∇. The Laplace operator Δ is then the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of the divergence and gradient operators:
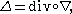
acting on scalar functions to produce scalar functions. Note that A = −Δ is a positive operator, whereas Δ is a dissipative operator.
Using spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, one can define a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
(1 − Δ)1/2 for the operator (1 − Δ). This square root satisfies the following relation involving the Sobolev H1-norm
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
and L2-norm
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for suitable scalar functions f:
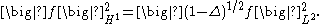
The Ornstein–Uhlenbeck operator
Often, when working on Rn, one works with respect to Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, which has many nice properties. However, remember that the aim is to work in infinite-dimensional spaces, and it is a fact that there is no infinite-dimensional Lebesgue measure
There is no infinite-dimensional Lebesgue measure
In mathematics, it is a theorem that there is no analogue of Lebesgue measure on an infinite-dimensional Banach space. Other kinds of measures are therefore used on infinite-dimensional spaces: often, the abstract Wiener space construction is used...
. Instead, if one is studying some separable Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
E, what does make sense is a notion of Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
; in particular, the abstract Wiener space
Abstract Wiener space
An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent" measure on an infinite-dimensional vector space. It is named after the American mathematician Norbert Wiener...
construction makes sense.
To get some intuition about what can be expected in the infinite-dimensional setting, consider standard Gaussian measure γn on Rn: for Borel subsets A of Rn,
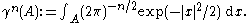
This makes (Rn, B(Rn), γn) into a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
; E will denoted expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to γn.
The gradient operator ∇ acts on a (differentiable) function φ : Rn → R to give a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
∇φ : Rn → Rn.
The divergence operator δ (to be more precise, δn, since it depends on the dimension) is now defined to be the adjoint of ∇ in the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
sense, in the Hilbert space L2(Rn, B(Rn), γn; R). In other words, δ acts on a vector field v : Rn → Rn to give a scalar function δv : Rn → R, and satisfies the formula
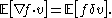
On the left, the product is the pointwise Euclidean dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of two vector fields; on the right, it is just the pointwise multiplication of two functions. Using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, one can check that δ acts on a vector field v with components vi, i = 1, ..., n, as follows:
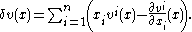
The change of notation from “div” to “δ” is for two reasons: first, δ is the notation used in infinite dimensions (the Malliavin calculus); secondly, δ is really the negative of the usual divergence.
The (finite-dimensional) Ornstein–Uhlenbeck operator L (or, to be more precise, Lm) is defined by
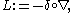
with the useful formula that for any f and g smooth enough for all the terms to make sense,
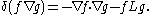
The Ornstein–Uhlenbeck operator L is related to the usual Laplacian Δ by
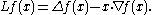
The Ornstein–Uhlenbeck operator for a separable Banach space
Consider now an abstract Wiener spaceAbstract Wiener space
An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent" measure on an infinite-dimensional vector space. It is named after the American mathematician Norbert Wiener...
E with Cameron-Martin Hilbert space H and Wiener measure γ. Let D denote the Malliavin derivative
Malliavin derivative
In mathematics, the Malliavin derivative is a notion of derivative in the Malliavin calculus. Intuitively, it is the notion of derivative appropriate to paths in classical Wiener space, which are "usually" not differentiable in the usual sense...
. The Malliavin derivative D is an unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
from L2(E, γ; R) into L2(E, γ; H) – in some sense, it measures “how random” a function on E is. The domain of D is not the whole of L2(E, γ; R), but is a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
, the Watanabe-Sobolev space, often denoted by
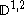(once differentiable in the sense of Malliavin, with derivative in L2).Again, δ is defined to be the adjoint of the gradient operator (in this case, the Malliavin derivative is playing the role of the gradient operator). The operator δ is also known the Skorokhod integral
Skorokhod integral
In mathematics, the Skorokhod integral, often denoted δ, is an operator of great importance in the theory of stochastic processes. It is named after the Ukrainian mathematician Anatoliy Skorokhod...
, which is an anticipating stochastic integral; it is this set-up that gives rise to the slogan “stochastic integrals are divergences”. δ satisfies the identity
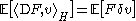
for all F in
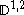and u in the domain of δ.Then the Ornstein–Uhlenbeck operator for E is the operator L defined by