PCF theory
Encyclopedia
PCF theory is the name of a mathematical
theory, introduced by Saharon , that deals with the cofinality
of the ultraproduct
s of ordered set
s. It gives strong upper bounds on the cardinalities of power sets of singular
cardinal
s, and has many more applications as well. The abbreviation "PCF" stands for "possible cofinalities
".
s, D is an ultrafilter
on A, then
we let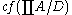
denote the cofinality of the ordered set of functions
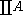where the ordering is defined as follows.
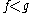if 
.
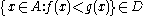pcf(A) is the set of cofinalities that occur if we consider all ultrafilters on A, that is,
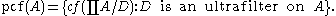
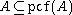. Shelah proved, that if 
, then pcf(A) has a largest element, and there are subsets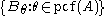 
of A such that for each ultrafilter D on A, 
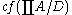is the least element θ of pcf(A) such that 
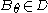. Consequently, 
.
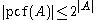Shelah also proved that if A is an interval of regular cardinals (i.e., A is the set of all regular cardinals between two cardinals), then pcf(A) is also an interval of regular cardinals and |pcf(A)|<|A|+4.
This implies the famous inequality
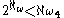
assuming that ℵωis strong limit
.
If λ is an infinite cardinal, then J<λ is the following ideal on A. B∈J<λ if
holds for every ultrafilter D with B∈D. Then J<λ is the ideal generated by the sets 
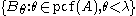. There exist scales, i.e., for every λ∈pcf(A) there is a sequence of length λ of elements of 
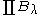which is both increasing and cofinal mod J<λ. This implies that the cofinality of 
under pointwise dominance is max(pcf(A)).
Another consequence is that if λ is singular and no regular cardinal less than λ is Jónsson
, then also λ+ is not Jónsson. In particular, there is a Jónsson algebra on ℵω+1, which settles an old conjecture.
A). This would imply that if ℵω is strong limit, then the sharp bound
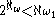
holds. The analogous bound
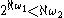
follows from Chang's conjecture
(Magidor
) or even from the nonexistence of a Kurepa tree (Shelah
).
A weaker, still unsolved conjecture states that if |A|A), then pcf(A) has no inaccessible limit point. This is equivalent to the statement that pcf(pcf(A))=pcf(A).
The original survey by Shelah, Cardinal arithmetic for skeptics, includes the following topics: almost free abelian groups, partition problems, failure of preservation of chain conditions in Boolean algebras under products, existence of Jónsson algebras, existence of entangled linear orders, equivalently narrow Boolean algebras, and the existence of nonisomorphic models equivalent in certain infinitary logics.
In the meantime, many further applications have been found in Set Theory, Model Theory, Algebra and Topology.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory, introduced by Saharon , that deals with the cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
of the ultraproduct
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
s of ordered set
Ordered set
In order theory in mathematics, a set with a binary relation R on its elements that is reflexive , antisymmetric and transitive is described as a partially ordered set or poset...
s. It gives strong upper bounds on the cardinalities of power sets of singular
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s, and has many more applications as well. The abbreviation "PCF" stands for "possible cofinalities
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
".
Main definitions
If A is an infinite set of regular cardinalRegular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
s, D is an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
on A, then
we let
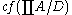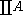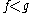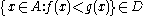denote the cofinality of the ordered set of functions where the ordering is defined as follows. if .pcf(A) is the set of cofinalities that occur if we consider all ultrafilters on A, that is,
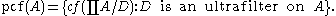
Main results
Obviously, pcf(A) consists of regular cardinals. Considering ultrafilters concentrated on elements of A, we get that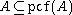. Shelah proved, that if , then pcf(A) has a largest element, and there are subsets 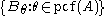of A such that for each ultrafilter D on A, 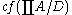is the least element θ of pcf(A) such that 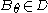. Consequently, 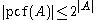.Shelah also proved that if A is an interval of regular cardinals (i.e., A is the set of all regular cardinals between two cardinals), then pcf(A) is also an interval of regular cardinals and |pcf(A)|<|A|+4.
This implies the famous inequality
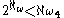
assuming that ℵωis strong limit
Limit cardinal
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
.
If λ is an infinite cardinal, then J<λ is the following ideal on A. B∈J<λ if
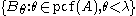holds for every ultrafilter D with B∈D. Then J<λ is the ideal generated by the sets . There exist scales, i.e., for every λ∈pcf(A) there is a sequence of length λ of elements of 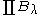which is both increasing and cofinal mod J<λ. This implies that the cofinality of under pointwise dominance is max(pcf(A)).Another consequence is that if λ is singular and no regular cardinal less than λ is Jónsson
Jónsson cardinal
In set theory, a Jónsson cardinal is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Jónsson if for every function f: [κ]...
, then also λ+ is not Jónsson. In particular, there is a Jónsson algebra on ℵω+1, which settles an old conjecture.
Unsolved problems
The most notorious conjecture in pcf theory states that |pcf(A)|=|A| holds for every set A of regular cardinals with |A|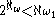holds. The analogous bound
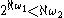
follows from Chang's conjecture
Chang's conjecture
In model theory, a branch of mathematical logic, Chang's conjecture, attributed to Chen Chung Chang by , states that every model of type for a countable language has an elementary submodel of type . A model is of type if it is of cardinality α and a unary relation is represented by a subset of...
(Magidor
Menachem Magidor
Menachem Magidor is an Israeli mathematician who specializes in mathematical logic, in particular set theory. He served as President of the Hebrew University of Jerusalem.- Biography :Menachem Magidor was born in Petah Tikva on January 24, 1946....
) or even from the nonexistence of a Kurepa tree (Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
).
A weaker, still unsolved conjecture states that if |A|
Applications
The theory has found a great deal of applications, besides cardinal arithmetic.The original survey by Shelah, Cardinal arithmetic for skeptics, includes the following topics: almost free abelian groups, partition problems, failure of preservation of chain conditions in Boolean algebras under products, existence of Jónsson algebras, existence of entangled linear orders, equivalently narrow Boolean algebras, and the existence of nonisomorphic models equivalent in certain infinitary logics.
In the meantime, many further applications have been found in Set Theory, Model Theory, Algebra and Topology.