
Packing in a hypergraph
Encyclopedia
In mathematics, a packing in a hypergraph is a partition
of the set of the hypergraph
's edges into a number of disjoint subsets such that no pair of edges in each subset share any vertex. There are two famous algorithms to achieve asymptotically optimal packing in k-uniform hypergraphs. One of them is a random greedy algorithm
which was proposed by Joel Spencer
. He used a branching process
to formally prove the optimal achievable bound under some side conditions. The other algorithm is called Rödl nibble and was proposed by Vojtěch Rödl
et al. They showed that the achievable packing by Rödl nibble is in some sense close to that of the random greedy algorithm.
was originally motivated through a conjecture by Paul Erdős
and Haim Hanani in 1963. Vojtech Rödl
proved their conjecture asymptotically under certain conditions in 1985. Pippenger and Joel Spencer
generalized Rödl's results using a random greedy algorithm
in 1989.
is denoted by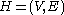 .
. 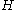 is called k-uniform hypergraph if every edge in
is called k-uniform hypergraph if every edge in 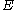 consists of exactly
consists of exactly 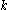 vertices.
vertices.
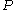 is a hypergraph packing if it is a subset of edges in H such that there is no pair of distinct edges with a common vertex.
is a hypergraph packing if it is a subset of edges in H such that there is no pair of distinct edges with a common vertex.
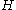 is a (
is a (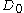 ,
, )-good hypergraph if there exists a
)-good hypergraph if there exists a 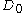 such that for all
such that for all 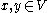 and
and 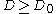 and both of the following conditions hold.
and both of the following conditions hold.
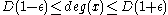
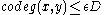
where deg of a vertex denotes the number of edges that contain that vertex and codeg of two distinct vertices denotes the number of edges that contain both vertices.
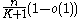 for a
for a 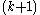 -uniform hypergraph under the following two conditions,
-uniform hypergraph under the following two conditions,
where is the total number of vertices. This result was shown by Pippenger and was later proved by Joel Spencer. To address the asymptotic hypergraph packing problem, Joel Spencer proposed a random greedy algorithm. In this algorithm, a branching process is used as the basis and it was shown that it almost always achieves an asymptotically optimal packing under the above side conditions.
is the total number of vertices. This result was shown by Pippenger and was later proved by Joel Spencer. To address the asymptotic hypergraph packing problem, Joel Spencer proposed a random greedy algorithm. In this algorithm, a branching process is used as the basis and it was shown that it almost always achieves an asymptotically optimal packing under the above side conditions.
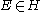 is independently and uniformly assigned a distinct real "birthtime"
is independently and uniformly assigned a distinct real "birthtime" 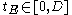 . The edges are taken one by one in the order of their birthtimes. The edge
. The edges are taken one by one in the order of their birthtimes. The edge 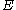 is accepted and included in
is accepted and included in 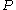 if it does not overlap any previously accepted edges. Obviously, the subset
if it does not overlap any previously accepted edges. Obviously, the subset  is a packing and it can be shown that its size is
is a packing and it can be shown that its size is 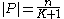 almost surely. To show that, let stop the process of adding new edges at time
almost surely. To show that, let stop the process of adding new edges at time  . For an arbitrary
. For an arbitrary 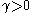 , pick
, pick 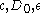 such that for any
such that for any 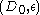 -good hypergraph
-good hypergraph 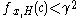 where
where 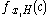 denotes the probability of vertex
denotes the probability of vertex  survival (a vertex survives if it is not in any edges in
survival (a vertex survives if it is not in any edges in 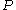 ) until time
) until time  . Obviously, in such a situation the expected number of
. Obviously, in such a situation the expected number of  surviving at time
surviving at time  is less than
is less than 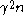 . As a result, the probability of
. As a result, the probability of  surviving being less than
surviving being less than 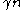 is higher than
is higher than 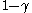 . In other words,
. In other words, 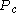 must include at least
must include at least 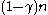 vertices which means that
vertices which means that 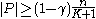 .
.
To complete the proof, it must be shown that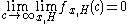 . For that, the asymptotic behavior of
. For that, the asymptotic behavior of  surviving is modeled by a continuous branching process. Fix
surviving is modeled by a continuous branching process. Fix 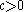 and begin with Eve with the birthdate of
and begin with Eve with the birthdate of  . Assume time goes backward so Eve gives birth in the interval of
. Assume time goes backward so Eve gives birth in the interval of 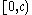 with a unit density Poisson distribution
with a unit density Poisson distribution
. The probability of Eve having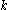 birth is
birth is 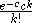 . By conditioning on
. By conditioning on 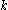 the birthtimes
the birthtimes 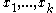 are independently and uniformly distributed on
are independently and uniformly distributed on 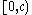 . Every birth given by Eve consists of
. Every birth given by Eve consists of 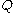 offspring all with the same birth time say
offspring all with the same birth time say  . The process is iterated for each offspring. It can be shown that for all
. The process is iterated for each offspring. It can be shown that for all 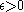 there exists a
there exists a 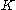 so that with a probability higher than
so that with a probability higher than 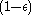 , Eve has at most
, Eve has at most 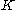 descendants.
descendants.
A rooted tree with the notions of parent, child, root, birthorder and wombmate shall be called a broodtree. Given a finite broodtree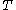 we say for each vertex that it survives or dies. A childless vertex survives. A vertex dies if and only if it has at least one brood all of whom survive. Let
we say for each vertex that it survives or dies. A childless vertex survives. A vertex dies if and only if it has at least one brood all of whom survive. Let 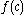 denote the probability that Eve survives in the broodtree
denote the probability that Eve survives in the broodtree 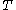 given by the above process. The objective is to show
given by the above process. The objective is to show 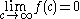 and then for any fixed
and then for any fixed  , it can be shown that
, it can be shown that 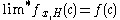 . These two relations complete our argument.
. These two relations complete our argument.
To show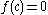 , let
, let 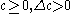 . For
. For 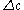 small,
small, 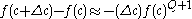 as, roughly, an Eve starting at time
as, roughly, an Eve starting at time 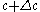 might have a birth in time interval
might have a birth in time interval 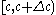 all of whose children survive while Eve has no births in
all of whose children survive while Eve has no births in 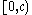 all of whose children survive. Letting
all of whose children survive. Letting 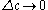 yields the differential equation
yields the differential equation 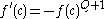 . The initial value
. The initial value 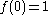 gives a unique solution
gives a unique solution 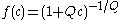 . Note that indeed
. Note that indeed 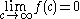 .
.
To prove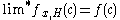 , consider a proceture we call History which either aborts or produces a broodtree. History contains a set
, consider a proceture we call History which either aborts or produces a broodtree. History contains a set 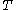 of vertices, initially
of vertices, initially 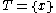 .
. 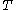 will have a broodtree structure with
will have a broodtree structure with  the root. The
the root. The 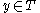 are either processed or unprocessed,
are either processed or unprocessed,  is initially unprocessed. To each
is initially unprocessed. To each 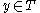 is assigned a birthtime
is assigned a birthtime 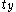 , we initialize
, we initialize 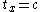 . History is to take an unprocessed
. History is to take an unprocessed 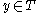 and process it as follows. For the value of all
and process it as follows. For the value of all 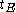 with
with 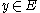 but with no
but with no 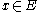 that has already been processed, if either some
that has already been processed, if either some 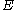 has
has 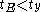 and
and 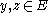 with
with 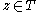 or some
or some 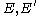 have
have 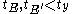 with
with 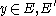 and
and 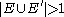 , then History is aborted. Otherwise for each
, then History is aborted. Otherwise for each 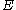 with
with 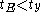 add all
add all 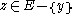 to
to 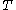 as wombmates with parent
as wombmates with parent 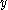 and common birthdate
and common birthdate 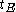 . Now
. Now 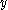 is considered processed. History halts, if not aborted, when all
is considered processed. History halts, if not aborted, when all 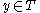 are processed. If History does not abort then root
are processed. If History does not abort then root  survives broodtree
survives broodtree 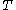 if and only if
if and only if  survives at time
survives at time  . For a fixed broodtree, let
. For a fixed broodtree, let 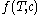 denote the probability that the branching process yields broodtree
denote the probability that the branching process yields broodtree 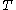 . Then the probability that History does not abort is
. Then the probability that History does not abort is 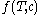 . By the finiteness of the branching process,
. By the finiteness of the branching process, 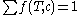 , the summation over all broodtrees
, the summation over all broodtrees 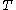 and History does not abort. The
and History does not abort. The 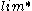 distribution of its broodtree approaches the braching process distribution. Thus
distribution of its broodtree approaches the braching process distribution. Thus 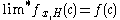 .
.
’s conjecture by a method called Rödl nibble. Rodl's result can be formulated in form of either packing or covering problem. For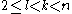 the covering number denoted by
the covering number denoted by 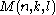 shows the minimal size of a family
shows the minimal size of a family  of k-element subsets of
of k-element subsets of 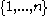 which have the property that every l-element set is contained in at least one
which have the property that every l-element set is contained in at least one 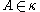 . Paul Erdős
. Paul Erdős
et al. conjecture was
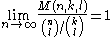 .
.
where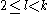 . This conjecture roughly means that a tactical configuration is asymptotically achievable. One may similarly define the packing number
. This conjecture roughly means that a tactical configuration is asymptotically achievable. One may similarly define the packing number 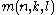 as the maximal size of a family
as the maximal size of a family  of k-element subsets of
of k-element subsets of 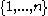 having the property that every l-element set is contained in at most one
having the property that every l-element set is contained in at most one 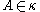 .
.
, Jeong Han Kim
, and Joel Spencer
also supply a good bound for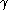 under the stronger
under the stronger 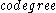 condition that every distinct pair
condition that every distinct pair 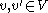 have at most one edge in common.
have at most one edge in common.
For a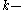 uniform,
uniform, 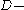 regular hypergraph on
regular hypergraph on  vertices, if
vertices, if 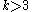 , there exists a packing
, there exists a packing 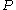 covering all vertices but at most
covering all vertices but at most 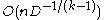 . If
. If 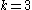 there exists a packing
there exists a packing 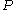 covering all vertices but at most
covering all vertices but at most 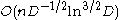 .
.
This bound is desirable in various applications, such as Steiner triple system.
A Steiner Triple System is a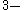 uniform, simple hypergraph in which every pair of vertices is contained in precisely one edge. Since a Steiner Triple System is clearly
uniform, simple hypergraph in which every pair of vertices is contained in precisely one edge. Since a Steiner Triple System is clearly 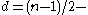 regular, the above bound supplies the following asymptotic improvement.
regular, the above bound supplies the following asymptotic improvement.
Any Steiner Triple System on vertices contains a packing covering all vertices but at most
vertices contains a packing covering all vertices but at most 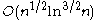 .
.
External links=
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set of the hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
's edges into a number of disjoint subsets such that no pair of edges in each subset share any vertex. There are two famous algorithms to achieve asymptotically optimal packing in k-uniform hypergraphs. One of them is a random greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
which was proposed by Joel Spencer
Joel Spencer
Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
. He used a branching process
Branching process
In probability theory, a branching process is a Markov process that models a population in which each individual in generation n produces some random number of individuals in generation n + 1, according to a fixed probability distribution that does not vary from individual to...
to formally prove the optimal achievable bound under some side conditions. The other algorithm is called Rödl nibble and was proposed by Vojtěch Rödl
Vojtěch Rödl
Vojtěch Rödl is a Czech mathematician, currently the Samuel Candler Dobbs Professor at Emory University, Atlanta, known for his work in combinatorics. He received his PhD from Charles University, Prague in 1976...
et al. They showed that the achievable packing by Rödl nibble is in some sense close to that of the random greedy algorithm.
History
The problem of finding the number of such subsets in a k-uniform hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
was originally motivated through a conjecture by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Haim Hanani in 1963. Vojtech Rödl
Vojtěch Rödl
Vojtěch Rödl is a Czech mathematician, currently the Samuel Candler Dobbs Professor at Emory University, Atlanta, known for his work in combinatorics. He received his PhD from Charles University, Prague in 1976...
proved their conjecture asymptotically under certain conditions in 1985. Pippenger and Joel Spencer
Joel Spencer
Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
generalized Rödl's results using a random greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
in 1989.
Definition and terminology
In the following definitions, the hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
is denoted by
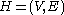 .
. 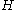 is called k-uniform hypergraph if every edge in
is called k-uniform hypergraph if every edge in 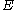 consists of exactly
consists of exactly 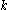 vertices.
vertices.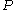 is a hypergraph packing if it is a subset of edges in H such that there is no pair of distinct edges with a common vertex.
is a hypergraph packing if it is a subset of edges in H such that there is no pair of distinct edges with a common vertex.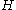 is a (
is a (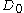 ,
, )-good hypergraph if there exists a
)-good hypergraph if there exists a 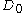 such that for all
such that for all 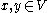 and
and 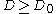 and both of the following conditions hold.
and both of the following conditions hold.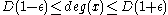
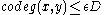
where deg of a vertex denotes the number of edges that contain that vertex and codeg of two distinct vertices denotes the number of edges that contain both vertices.
Theorem
There exists an asymptotic packing P of size at least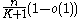 for a
for a 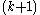 -uniform hypergraph under the following two conditions,
-uniform hypergraph under the following two conditions,- All vertices have the degree of
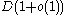 in which
in which 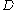 tends to infinity.
tends to infinity. - For every pair of vertices shares only
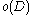 common edges.
common edges.
where
 is the total number of vertices. This result was shown by Pippenger and was later proved by Joel Spencer. To address the asymptotic hypergraph packing problem, Joel Spencer proposed a random greedy algorithm. In this algorithm, a branching process is used as the basis and it was shown that it almost always achieves an asymptotically optimal packing under the above side conditions.
is the total number of vertices. This result was shown by Pippenger and was later proved by Joel Spencer. To address the asymptotic hypergraph packing problem, Joel Spencer proposed a random greedy algorithm. In this algorithm, a branching process is used as the basis and it was shown that it almost always achieves an asymptotically optimal packing under the above side conditions.Asymptotic packing algorithms
There are two famous algorithms for asymptotic packing of k-uniform hypegraphs which are random greedy algorithm via branching process and Rödl nibble.Random greedy algorithm via branching process
Every edge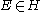 is independently and uniformly assigned a distinct real "birthtime"
is independently and uniformly assigned a distinct real "birthtime" 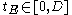 . The edges are taken one by one in the order of their birthtimes. The edge
. The edges are taken one by one in the order of their birthtimes. The edge 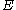 is accepted and included in
is accepted and included in 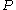 if it does not overlap any previously accepted edges. Obviously, the subset
if it does not overlap any previously accepted edges. Obviously, the subset  is a packing and it can be shown that its size is
is a packing and it can be shown that its size is 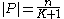 almost surely. To show that, let stop the process of adding new edges at time
almost surely. To show that, let stop the process of adding new edges at time  . For an arbitrary
. For an arbitrary 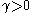 , pick
, pick 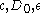 such that for any
such that for any 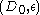 -good hypergraph
-good hypergraph 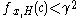 where
where 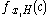 denotes the probability of vertex
denotes the probability of vertex  survival (a vertex survives if it is not in any edges in
survival (a vertex survives if it is not in any edges in 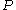 ) until time
) until time  . Obviously, in such a situation the expected number of
. Obviously, in such a situation the expected number of  surviving at time
surviving at time  is less than
is less than 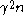 . As a result, the probability of
. As a result, the probability of  surviving being less than
surviving being less than 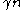 is higher than
is higher than 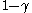 . In other words,
. In other words, 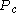 must include at least
must include at least 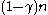 vertices which means that
vertices which means that 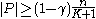 .
.To complete the proof, it must be shown that
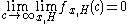 . For that, the asymptotic behavior of
. For that, the asymptotic behavior of  surviving is modeled by a continuous branching process. Fix
surviving is modeled by a continuous branching process. Fix 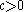 and begin with Eve with the birthdate of
and begin with Eve with the birthdate of  . Assume time goes backward so Eve gives birth in the interval of
. Assume time goes backward so Eve gives birth in the interval of 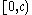 with a unit density Poisson distribution
with a unit density Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
. The probability of Eve having
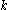 birth is
birth is 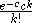 . By conditioning on
. By conditioning on 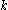 the birthtimes
the birthtimes 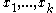 are independently and uniformly distributed on
are independently and uniformly distributed on 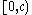 . Every birth given by Eve consists of
. Every birth given by Eve consists of 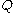 offspring all with the same birth time say
offspring all with the same birth time say  . The process is iterated for each offspring. It can be shown that for all
. The process is iterated for each offspring. It can be shown that for all 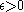 there exists a
there exists a 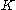 so that with a probability higher than
so that with a probability higher than 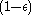 , Eve has at most
, Eve has at most 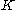 descendants.
descendants.A rooted tree with the notions of parent, child, root, birthorder and wombmate shall be called a broodtree. Given a finite broodtree
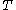 we say for each vertex that it survives or dies. A childless vertex survives. A vertex dies if and only if it has at least one brood all of whom survive. Let
we say for each vertex that it survives or dies. A childless vertex survives. A vertex dies if and only if it has at least one brood all of whom survive. Let 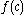 denote the probability that Eve survives in the broodtree
denote the probability that Eve survives in the broodtree 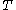 given by the above process. The objective is to show
given by the above process. The objective is to show 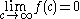 and then for any fixed
and then for any fixed  , it can be shown that
, it can be shown that 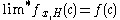 . These two relations complete our argument.
. These two relations complete our argument.To show
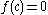 , let
, let 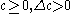 . For
. For 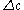 small,
small, 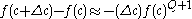 as, roughly, an Eve starting at time
as, roughly, an Eve starting at time 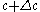 might have a birth in time interval
might have a birth in time interval 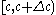 all of whose children survive while Eve has no births in
all of whose children survive while Eve has no births in 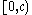 all of whose children survive. Letting
all of whose children survive. Letting 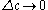 yields the differential equation
yields the differential equation 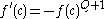 . The initial value
. The initial value 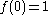 gives a unique solution
gives a unique solution 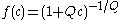 . Note that indeed
. Note that indeed 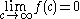 .
.To prove
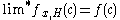 , consider a proceture we call History which either aborts or produces a broodtree. History contains a set
, consider a proceture we call History which either aborts or produces a broodtree. History contains a set 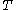 of vertices, initially
of vertices, initially 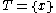 .
. 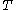 will have a broodtree structure with
will have a broodtree structure with  the root. The
the root. The 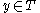 are either processed or unprocessed,
are either processed or unprocessed,  is initially unprocessed. To each
is initially unprocessed. To each 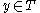 is assigned a birthtime
is assigned a birthtime 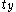 , we initialize
, we initialize 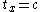 . History is to take an unprocessed
. History is to take an unprocessed 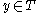 and process it as follows. For the value of all
and process it as follows. For the value of all 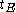 with
with 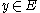 but with no
but with no 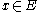 that has already been processed, if either some
that has already been processed, if either some 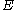 has
has 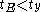 and
and 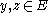 with
with 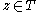 or some
or some 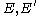 have
have 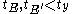 with
with 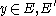 and
and 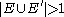 , then History is aborted. Otherwise for each
, then History is aborted. Otherwise for each 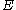 with
with 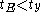 add all
add all 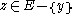 to
to 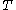 as wombmates with parent
as wombmates with parent 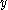 and common birthdate
and common birthdate 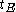 . Now
. Now 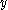 is considered processed. History halts, if not aborted, when all
is considered processed. History halts, if not aborted, when all 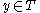 are processed. If History does not abort then root
are processed. If History does not abort then root  survives broodtree
survives broodtree 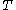 if and only if
if and only if  survives at time
survives at time  . For a fixed broodtree, let
. For a fixed broodtree, let 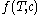 denote the probability that the branching process yields broodtree
denote the probability that the branching process yields broodtree 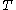 . Then the probability that History does not abort is
. Then the probability that History does not abort is 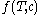 . By the finiteness of the branching process,
. By the finiteness of the branching process, 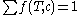 , the summation over all broodtrees
, the summation over all broodtrees 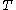 and History does not abort. The
and History does not abort. The 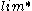 distribution of its broodtree approaches the braching process distribution. Thus
distribution of its broodtree approaches the braching process distribution. Thus 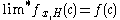 .
.Rödl nibble
In 1985, Rödl proved Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
’s conjecture by a method called Rödl nibble. Rodl's result can be formulated in form of either packing or covering problem. For
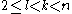 the covering number denoted by
the covering number denoted by 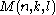 shows the minimal size of a family
shows the minimal size of a family  of k-element subsets of
of k-element subsets of 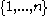 which have the property that every l-element set is contained in at least one
which have the property that every l-element set is contained in at least one 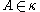 . Paul Erdős
. Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
et al. conjecture was
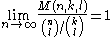 .
.where
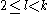 . This conjecture roughly means that a tactical configuration is asymptotically achievable. One may similarly define the packing number
. This conjecture roughly means that a tactical configuration is asymptotically achievable. One may similarly define the packing number 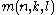 as the maximal size of a family
as the maximal size of a family  of k-element subsets of
of k-element subsets of 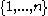 having the property that every l-element set is contained in at most one
having the property that every l-element set is contained in at most one 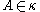 .
.Packing under the stronger condition
In 1997, Noga AlonNoga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
, Jeong Han Kim
Jeong Han Kim
Jeong Han Kim is a South Korean mathematician specializing in combinatorics and computational mathematics. He studied physics and mathematical physics at Yonsei University, and earned his Ph.D in mathematics at Rutgers University...
, and Joel Spencer
Joel Spencer
Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
also supply a good bound for
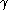 under the stronger
under the stronger 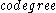 condition that every distinct pair
condition that every distinct pair 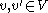 have at most one edge in common.
have at most one edge in common.For a
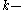 uniform,
uniform, 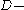 regular hypergraph on
regular hypergraph on  vertices, if
vertices, if 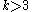 , there exists a packing
, there exists a packing 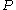 covering all vertices but at most
covering all vertices but at most 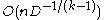 . If
. If 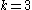 there exists a packing
there exists a packing 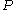 covering all vertices but at most
covering all vertices but at most 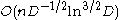 .
.This bound is desirable in various applications, such as Steiner triple system.
A Steiner Triple System is a
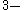 uniform, simple hypergraph in which every pair of vertices is contained in precisely one edge. Since a Steiner Triple System is clearly
uniform, simple hypergraph in which every pair of vertices is contained in precisely one edge. Since a Steiner Triple System is clearly 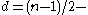 regular, the above bound supplies the following asymptotic improvement.
regular, the above bound supplies the following asymptotic improvement.Any Steiner Triple System on
 vertices contains a packing covering all vertices but at most
vertices contains a packing covering all vertices but at most 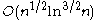 .
.See also
- Branching processBranching processIn probability theory, a branching process is a Markov process that models a population in which each individual in generation n produces some random number of individuals in generation n + 1, according to a fixed probability distribution that does not vary from individual to...
- Independent setIndependent set (graph theory)In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
- Graph coloringGraph coloringIn graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
- Covering number
- Set packingSet packingSet packing is a classical NP-complete problem in computational complexity theory and combinatorics, and was one of Karp's 21 NP-complete problems.Suppose we have a finite set S and a list of subsets of S...
- Ramsey's theoremRamsey's theoremIn combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
- Set cover problemSet cover problemThe set covering problem is a classical question in computer science and complexity theory.It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms...
- Sphere packingSphere packingIn geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
- Steiner systemSteiner system250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
External links=

