
Paneitz operator
Encyclopedia
In the mathematical
field of differential geometry, the Paneitz operator is a fourth-order differential operator
defined on a Riemannian manifold
of dimension n. It is named after Stephen Paneitz, who discovered it in 1983, and whose preprint was later published posthumously in . It is given by the formula
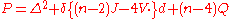
where Δ is the Laplace–Beltrami operator, d is the exterior derivative
, δ is its formal adjoint, V is the Schouten tensor, J is the trace of the Schouten tensor, and the dot denotes tensor contraction on either index. Here Q is the scalar invariant
which in four dimensions yields the Q-curvature.
The operator is especially important in conformal geometry
, because in a suitable sense it depends only on the conformal structure. Another operator of this kind is the conformal Laplacian. But, whereas the conformal Laplacian is second-order, with leading symbol
a multiple of the Laplace–Beltrami operator, the Paneitz operator is fourth-order, with leading symbol the square of the Laplace–Beltrami operator. The Paneitz operator is conformally invariant in the sense that it sends conformal densities
of weight to conformal densities of weight . Concretely, using the canonical trivialization of the density bundles in the presence of a metric, the Paneitz operator P can be represented in terms of a representative the Riemannian metric g as an ordinary operator on functions that transforms according under a conformal change according to the rule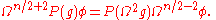
The operator was originally derived by working out specifically the lower-order correction terms in order to ensure conformal invariance. Subsequent investigations have situated the Paneitz operator into a hierarchy of analogous conformally invariant operators on densities: the GJMS operator
s.
The Paneitz operator has been most thoroughly studied in dimension four where it appears naturally in connection with extremal problems for the functional determinant
of the Laplacian (via the Polyakov formula
; see ). In dimension four only, the Paneitz operator is the "critical" GJMS operator, meaning that there is a residual scalar piece (the Q curvature) that can only be recovered by asymptotic analysis. The Paneitz operator appears in extremal problems for the Moser–Trudinger inequality in dimension four as well
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry, the Paneitz operator is a fourth-order differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
defined on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of dimension n. It is named after Stephen Paneitz, who discovered it in 1983, and whose preprint was later published posthumously in . It is given by the formula
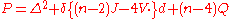
where Δ is the Laplace–Beltrami operator, d is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, δ is its formal adjoint, V is the Schouten tensor, J is the trace of the Schouten tensor, and the dot denotes tensor contraction on either index. Here Q is the scalar invariant

which in four dimensions yields the Q-curvature.
The operator is especially important in conformal geometry
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
, because in a suitable sense it depends only on the conformal structure. Another operator of this kind is the conformal Laplacian. But, whereas the conformal Laplacian is second-order, with leading symbol
Symbol of a differential operator
In mathematics, the symbol of a linear differential operator associates to a differential operator a polynomial by, roughly speaking, replacing each partial derivative by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this...
a multiple of the Laplace–Beltrami operator, the Paneitz operator is fourth-order, with leading symbol the square of the Laplace–Beltrami operator. The Paneitz operator is conformally invariant in the sense that it sends conformal densities
Density on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
of weight to conformal densities of weight . Concretely, using the canonical trivialization of the density bundles in the presence of a metric, the Paneitz operator P can be represented in terms of a representative the Riemannian metric g as an ordinary operator on functions that transforms according under a conformal change according to the rule
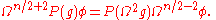
The operator was originally derived by working out specifically the lower-order correction terms in order to ensure conformal invariance. Subsequent investigations have situated the Paneitz operator into a hierarchy of analogous conformally invariant operators on densities: the GJMS operator
GJMS operator
In the mathematical field of differential geometry, the GJMS operators are a family of differential operators, that are defined on a Riemannian manifold. In an appropriate sense, they depend only on the conformal structure of the manifold. The GJMS operators generalize the Paneitz operator and...
s.
The Paneitz operator has been most thoroughly studied in dimension four where it appears naturally in connection with extremal problems for the functional determinant
Functional determinant
In mathematics, if S is a linear operator mapping a function space V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant. The corresponding quantity det is called the functional determinant of S.There are several formulas for the functional...
of the Laplacian (via the Polyakov formula
Polyakov formula
In differential geometry and mathematical physics , the Polyakov formula expresses the conformal variation of the zeta functional determinant of a Riemannian manifold. The corresponding density is local, and therefore is a Riemannian curvature invariant...
; see ). In dimension four only, the Paneitz operator is the "critical" GJMS operator, meaning that there is a residual scalar piece (the Q curvature) that can only be recovered by asymptotic analysis. The Paneitz operator appears in extremal problems for the Moser–Trudinger inequality in dimension four as well
See also
- Calabi conjectureCalabi conjectureIn mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by ....
- Positive mass conjecturePositive energy theoremIn general relativity, the positive energy theorem states that, assuming the dominant energy condition, the mass of an asymptotically flat spacetime is non-negative; furthermore, the mass is zero only for Minkowski spacetime...
- Yamabe conjecture
- Monge-Ampere equationMonge-Ampère equationIn mathematics, a Monge–Ampère equation is a nonlinear second order partial differential equation of special kind. A second order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant of the Hessian matrix of u and in the second order...
s

