Pearson's chi-squared test
Encyclopedia
Pearson's chi-squared test (χ
) is the best-known of several chi-squared tests – statistical
procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson
in 1900. In contexts where it is important to make a distinction between the test statistic
and its distribution, names similar to Pearson Χ-squared test or statistic are used.
It tests a null hypothesis
stating that the frequency distribution
of certain event
s observed in a sample
is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable
. A simple example is the hypothesis that an ordinary six-sided is "fair", i.e., all six outcomes are equally likely to occur.
and tests of independence.
The first step in the chi-squared test is to calculate the chi-squared statistic
. In order to avoid ambiguity, the value of the test-statistic is denoted by
rather than 
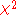(which is either an uppercase chi
instead of lowercase, or an upper case roman X); this also serves as a reminder that the distribution of the test statistic is not exactly that of a chi-squared random variable. However some authors do use the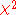
notation for the test statistic. An exact test which does not rely on using the approximate 
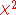distribution is Fisher's exact test
: this is substantially more accurate in evaluating the significance level of the test, especially with small numbers of observations.
The chi-squared statistic is calculated by finding the difference between each observed and theoretical frequency for each possible outcome, squaring them, dividing each by the theoretical frequency, and taking the sum of the results. A second important part of determining the test statistic is to define the degrees of freedom
of the test: this is essentially the number of observed frequencies adjusted for the effect of using some of those observations to define the theoretical frequencies.
observations are divided among 
cells. A simple application is to test the hypothesis that, in the general population, values would occur in each cell with equal frequency. The "theoretical frequency" for any cell (under the null hypothesis of a discrete uniform distribution) is thus calculated as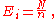
and the reduction in the degrees of freedom is
, notionally because the observed frequencies 
are constrained to sum to 
.
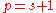, where 
is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution, 
, and when checking a normal distribution (where the parameters are mean and standard deviation), 
. In other words, there will be 
degrees of freedom, where 
is the number of categories.
It should be noted that the degrees of freedom are not based on the number of observations as with a Student's t or F-distribution. For example, if testing for a fair, six-sided die, there would be five degrees of freedom because there are six categories/parameters (each number). The number of times the die is rolled will have absolutely no effect on the number of degrees of freedom.
where
= Pearson's cumulative test statistic, which asymptotically approaches a 
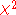distribution.
= an observed frequency;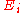
= an expected (theoretical) frequency, asserted by the null hypothesis;
= the number of cells in the table.
The chi-squared statistic can then be used to calculate a p-value
by comparing the value of the statistic to a chi-squared distribution. The number of degrees of freedom
is equal to the number of cells
, minus the reduction in degrees of freedom, 
.
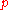The result about the number of degrees of freedom is valid when the original data was multinomial and hence the estimated parameters are efficient for minimizing the chi-squared statistic. More generally however, when maximum likelihood estimation does not coincide with minimum chi-squared estimation, the distribution will lie somewhere between a chi-squared distribution with
and 
degrees of freedom (See for instance Chernoff and Lehmann, 1954).
, one would instead use a Dirichlet distribution as conjugate prior
. If one took a uniform prior, then the maximum likelihood estimate for the population probability is the observed probability, and one may compute a credible region around this or another estimate.
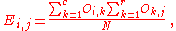
where N is the total sample size (the sum of all cells in the table). The value of the test-statistic is
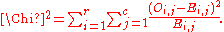
Fitting the model of "independence" reduces the number of degrees of freedom by p = r + c − 1. The number of degrees of freedom
is equal to the number of cells rc, minus the reduction in degrees of freedom, p, which reduces to (r − 1)(c − 1).
For the test of independence, a chi-squared probability of less than or equal to 0.05 (or the chi-squared statistic being at or larger than the 0.05 critical point) is commonly interpreted by applied workers as justification for rejecting the null hypothesis that the row variable is independent of the column variable.
The alternative hypothesis corresponds to the variables having an association or relationship where the structure of this relationship is not specified.
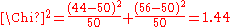
If the null hypothesis is true (i.e., men and women are chosen with equal probability in the sample), the test statistic will be drawn from a chi-squared distribution with one degree of freedom
. Though one might expect two degrees of freedom (one each for the men and women), we must take into account that the total number of men and women is constrained (100), and thus there is only one degree of freedom (2 − 1). Alternatively, if the male count is known the female count is determined, and vice-versa.
Consultation of the chi-squared distribution for 1 degree of freedom shows that the probability
of observing this difference (or a more extreme difference than this) if men and women are equally numerous in the population is approximately 0.23. This probability is higher than conventional criteria for statistical significance
(.001-.05), so normally we would not reject the null hypothesis that the number of men in the population is the same as the number of women (i.e. we would consider our sample within the range of what we'd expect for a 50/50 male/female ratio.)
In cases where the expected value, E, is found to be small (indicating either a small underlying population probability, or a small number of observations), the normal approximation of the multinomial distribution can fail, and in such cases it is found to be more appropriate to use the G-test
, a likelihood ratio
-based test statistic. Where the total sample size is small, it is necessary to use an appropriate exact test, typically either the binomial test
or (for contingency tables) Fisher's exact test
; but note that this test assumes fixed and known marginal totals.
(k − 1)(j − 1) degrees of freedom.
This approximation arises as the true distribution, under the null hypothesis, if the expected value is given by a multinomial distribution. For large sample sizes, the central limit theorem
says this distribution tends toward a certain multivariate normal distribution.
where
In the above example the hypothesised probability of a male observation is 0.5, with 100 samples. Thus we expect to observe 50 males.
If n is sufficiently large, the above binomial distribution may be approximated by a Gaussian (normal) distribution and thus the Pearson test statistic approximates a chi-squared distribution,
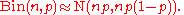
Let O1 be the number of observations from the sample that are in the first cell. The Pearson test statistic can be expressed as
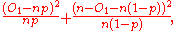
which can in turn be expressed as
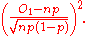
By the normal approximation to a binomial this is the squared of one standard normal variate, and hence is distributed as chi-squared with 1 degree of freedom. Note that the denominator is one standard deviation of the Gaussian approximation, so can be written
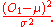
So as consistent with the meaning of the chi-squared distribution, we are measuring how probable the observed number of standard deviations away from the mean is under the Gaussian approximation (which is a good approximation for large n).
The chi-squared distribution is then integrated on the right of the statistic value to obtain the P-value
, which is equal to the probability of getting a statistic equal or bigger than the observed one, assuming the null hypothesis.
containing two rows and two columns, the test is equivalent to a Z-test
of proportions.
Chi (letter)
Chi is the 22nd letter of the Greek alphabet, pronounced as in English.-Greek:-Ancient Greek:Its value in Ancient Greek was an aspirated velar stop .-Koine Greek:...
) is the best-known of several chi-squared tests – statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson
Karl Pearson
Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....
in 1900. In contexts where it is important to make a distinction between the test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
and its distribution, names similar to Pearson Χ-squared test or statistic are used.
It tests a null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
stating that the frequency distribution
Frequency distribution
In statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of...
of certain event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
s observed in a sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable
Level of measurement
The "levels of measurement", or scales of measure are expressions that typically refer to the theory of scale types developed by the psychologist Stanley Smith Stevens. Stevens proposed his theory in a 1946 Science article titled "On the theory of scales of measurement"...
. A simple example is the hypothesis that an ordinary six-sided is "fair", i.e., all six outcomes are equally likely to occur.
Definition
Pearson's chi-squared is used to assess two types of comparison: tests of goodness of fitGoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
and tests of independence.
- A test of goodness of fit establishes whether or not an observed frequency distributionFrequency distributionIn statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of...
differs from a theoretical distribution. - A test of independence assesses whether paired observations on two variables, expressed in a contingency tableContingency tableIn statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
, are independent of each other—for example, whether people from different regions differ in the frequency with which they report that they support a political candidate.
The first step in the chi-squared test is to calculate the chi-squared statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
. In order to avoid ambiguity, the value of the test-statistic is denoted by
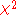rather than (which is either an uppercase chiChi (letter)
Chi is the 22nd letter of the Greek alphabet, pronounced as in English.-Greek:-Ancient Greek:Its value in Ancient Greek was an aspirated velar stop .-Koine Greek:...
instead of lowercase, or an upper case roman X); this also serves as a reminder that the distribution of the test statistic is not exactly that of a chi-squared random variable. However some authors do use the
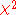notation for the test statistic. An exact test which does not rely on using the approximate 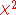distribution is Fisher's exact testFisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
: this is substantially more accurate in evaluating the significance level of the test, especially with small numbers of observations.
The chi-squared statistic is calculated by finding the difference between each observed and theoretical frequency for each possible outcome, squaring them, dividing each by the theoretical frequency, and taking the sum of the results. A second important part of determining the test statistic is to define the degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
of the test: this is essentially the number of observed frequencies adjusted for the effect of using some of those observations to define the theoretical frequencies.
Discrete uniform distribution
In this case observations are divided among cells. A simple application is to test the hypothesis that, in the general population, values would occur in each cell with equal frequency. The "theoretical frequency" for any cell (under the null hypothesis of a discrete uniform distribution) is thus calculated as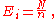and the reduction in the degrees of freedom is
, notionally because the observed frequencies are constrained to sum to .Other distributions
When testing whether observations are random variables whose distribution belongs to a given family of distributions, the "theoretical frequencies" are calculated using a distribution from that family fitted in some standard way. The reduction in the degrees of freedom is calculated as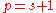, where is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution, , and when checking a normal distribution (where the parameters are mean and standard deviation), . In other words, there will be degrees of freedom, where is the number of categories.It should be noted that the degrees of freedom are not based on the number of observations as with a Student's t or F-distribution. For example, if testing for a fair, six-sided die, there would be five degrees of freedom because there are six categories/parameters (each number). The number of times the die is rolled will have absolutely no effect on the number of degrees of freedom.
Calculating the test-statistic
The value of the test-statistic iswhere
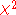= Pearson's cumulative test statistic, which asymptotically approaches a distribution. = an observed frequency;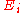 = an expected (theoretical) frequency, asserted by the null hypothesis; = the number of cells in the table.The chi-squared statistic can then be used to calculate a p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
by comparing the value of the statistic to a chi-squared distribution. The number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
is equal to the number of cells
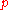, minus the reduction in degrees of freedom, .The result about the number of degrees of freedom is valid when the original data was multinomial and hence the estimated parameters are efficient for minimizing the chi-squared statistic. More generally however, when maximum likelihood estimation does not coincide with minimum chi-squared estimation, the distribution will lie somewhere between a chi-squared distribution with
and degrees of freedom (See for instance Chernoff and Lehmann, 1954).Bayesian method
In Bayesian statisticsBayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, one would instead use a Dirichlet distribution as conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
. If one took a uniform prior, then the maximum likelihood estimate for the population probability is the observed probability, and one may compute a credible region around this or another estimate.
Test of independence
In this case, an "observation" consists of the values of two outcomes and the null hypothesis is that the occurrence of these outcomes is statistically independent. Each observation is allocated to one cell of a two-dimensional array of cells (called a table) according to the values of the two outcomes. If there are r rows and c columns in the table, the "theoretical frequency" for a cell, given the hypothesis of independence, is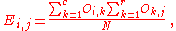where N is the total sample size (the sum of all cells in the table). The value of the test-statistic is
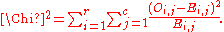
Fitting the model of "independence" reduces the number of degrees of freedom by p = r + c − 1. The number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
is equal to the number of cells rc, minus the reduction in degrees of freedom, p, which reduces to (r − 1)(c − 1).
For the test of independence, a chi-squared probability of less than or equal to 0.05 (or the chi-squared statistic being at or larger than the 0.05 critical point) is commonly interpreted by applied workers as justification for rejecting the null hypothesis that the row variable is independent of the column variable.
The alternative hypothesis corresponds to the variables having an association or relationship where the structure of this relationship is not specified.
Assumptions
The chi-squared test, when used with the standard approximation that a chi-squared distribution is applicable, has the following assumptions:- Simple random sampleSimple random sampleIn statistics, a simple random sample is a subset of individuals chosen from a larger set . Each individual is chosen randomly and entirely by chance, such that each individual has the same probability of being chosen at any stage during the sampling process, and each subset of k individuals has...
– The sample data is a random sampling from a fixed distribution or population where each member of the population has an equal probability of selection. Variants of the test have been developed for complex samples, such as where the data is weighted.
- Sample size (whole table) – A sample with a sufficiently large size is assumed. If a chi squared test is conducted on a sample with a smaller size, then the chi squared test will yield an inaccurate inference. The researcher, by using chi squared test on small samples, might end up committing a Type II error.
- Expected cell count – Adequate expected cell counts. Some require 5 or more, and others require 10 or more. A common rule is 5 or more in all cells of a 2-by-2 table, and 5 or more in 80% of cells in larger tables, but no cells with zero expected count. When this assumption is not met, Yates's correction is applied.
- Independence – The observations are always assumed to be independent of each other. This means chi-squared cannot be used to test correlated data (like matched pairs or panel data). In those cases you might want to turn to McNemar's testMcNemar's testIn statistics, McNemar's test is a non-parametric method used on nominal data. It is applied to 2 × 2 contingency tables with a dichotomous trait, with matched pairs of subjects, to determine whether the row and column marginal frequencies are equal...
.
Goodness of fit
For example, to test the hypothesis that a random sample of 100 people has been drawn from a population in which men and women are equal in frequency, the observed number of men and women would be compared to the theoretical frequencies of 50 men and 50 women. If there were 44 men in the sample and 56 women, then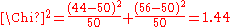If the null hypothesis is true (i.e., men and women are chosen with equal probability in the sample), the test statistic will be drawn from a chi-squared distribution with one degree of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
. Though one might expect two degrees of freedom (one each for the men and women), we must take into account that the total number of men and women is constrained (100), and thus there is only one degree of freedom (2 − 1). Alternatively, if the male count is known the female count is determined, and vice-versa.
Consultation of the chi-squared distribution for 1 degree of freedom shows that the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of observing this difference (or a more extreme difference than this) if men and women are equally numerous in the population is approximately 0.23. This probability is higher than conventional criteria for statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
(.001-.05), so normally we would not reject the null hypothesis that the number of men in the population is the same as the number of women (i.e. we would consider our sample within the range of what we'd expect for a 50/50 male/female ratio.)
Problems
The approximation to the chi-squared distribution breaks down if expected frequencies are too low. It will normally be acceptable so long as no more than 20% of the events have expected frequencies below 5. Where there is only 1 degree of freedom, the approximation is not reliable if expected frequencies are below 10. In this case, a better approximation can be obtained by reducing the absolute value of each difference between observed and expected frequencies by 0.5 before squaring; this is called Yates's correction for continuity.In cases where the expected value, E, is found to be small (indicating either a small underlying population probability, or a small number of observations), the normal approximation of the multinomial distribution can fail, and in such cases it is found to be more appropriate to use the G-test
G-test
In statistics, G-tests are likelihood-ratio or maximum likelihood statistical significance tests that are increasingly being used in situations where chi-squared tests were previously recommended....
, a likelihood ratio
Likelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
-based test statistic. Where the total sample size is small, it is necessary to use an appropriate exact test, typically either the binomial test
Binomial test
In statistics, the binomial test is an exact test of the statistical significance of deviations from a theoretically expected distribution of observations into two categories.-Common use:...
or (for contingency tables) Fisher's exact test
Fisher's exact test
Fisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
; but note that this test assumes fixed and known marginal totals.
Distribution
The null distribution of the Pearson statistic with j rows and k columns is approximated by the chi-squared distribution with(k − 1)(j − 1) degrees of freedom.
This approximation arises as the true distribution, under the null hypothesis, if the expected value is given by a multinomial distribution. For large sample sizes, the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
says this distribution tends toward a certain multivariate normal distribution.
Two cells
In the special case where there are only two cells in the table, the expected values follow a binomial distribution,where
- p = probability, under the null hypothesis,
- n = number of observations in the sample.
In the above example the hypothesised probability of a male observation is 0.5, with 100 samples. Thus we expect to observe 50 males.
If n is sufficiently large, the above binomial distribution may be approximated by a Gaussian (normal) distribution and thus the Pearson test statistic approximates a chi-squared distribution,
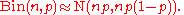
Let O1 be the number of observations from the sample that are in the first cell. The Pearson test statistic can be expressed as
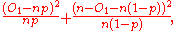
which can in turn be expressed as
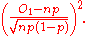
By the normal approximation to a binomial this is the squared of one standard normal variate, and hence is distributed as chi-squared with 1 degree of freedom. Note that the denominator is one standard deviation of the Gaussian approximation, so can be written
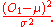
So as consistent with the meaning of the chi-squared distribution, we are measuring how probable the observed number of standard deviations away from the mean is under the Gaussian approximation (which is a good approximation for large n).
The chi-squared distribution is then integrated on the right of the statistic value to obtain the P-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
, which is equal to the probability of getting a statistic equal or bigger than the observed one, assuming the null hypothesis.
Two-by-two contingency tables
When the test is applied to a contingency tableContingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
containing two rows and two columns, the test is equivalent to a Z-test
Z-test
A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
of proportions.
Many cells
Similar arguments as above lead to the desired result. Each cell (except the final one, whose value is completely determined by the others) is treated as an independent binomial variable, and their contributions are summed and each contributes one degree of freedom.See also
- Degrees of freedom (statistics)Degrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
, including Degrees of freedom (statistics)#Effective degrees of freedom for correlated observations and regularized models - Fisher's exact testFisher's exact testFisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
- Median testMedian testIn statistics, Mood's median test is a special case of Pearson's chi-squared test. It is a nonparametric test that tests the null hypothesis that the medians of the populations from which two samples are drawn are identical...
- Chi-squared test
- Chi-squared nomogram
- Deviance (statistics), another measure of the quality of fit.
- Yates's correction for continuity
- Mann–Whitney U
- Cramér's V - a measure of correlation for the chi-squared test.
External links
- A video comparison of Chi-Squared Fitting Engines in Excel
- Chi-squared tests of contingency tables
- Chi-Squared Applet Calculator
- Sampling Distribution of the Sample Chi-Squared Statistic — a Java appletJava appletA Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
showing the sampling distribution of the Pearson test statistic. - Online Chi-Squared Test for uniform distribution
- Chi-Squared distribution table
- A tutorial on the chi-squared test devised for Oxford University psychology students