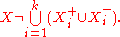Ping-pong lemma
Encyclopedia
In mathematics
, the ping-pong lemma, or table-tennis lemma, is any of several mathematical statements that ensure that several elements in a group acting
on a set freely generate
a free
subgroup
of that group.
who used it to study subgroups of Kleinian group
s, that is, of discrete groups of isometries of the hyperbolic 3-space or, equivalently Möbius transformations of the Riemann sphere
. The ping-pong lemma was a key tool used by Jacques Tits
in his 1972 paper containing the proof of a famous result now known as the Tits alternative
. The result states that a finitely generated linear group is either virtually
solvable
or contains a free
subgroup
of rank two. The ping-pong lemma and its variations are widely used in geometric topology
and geometric group theory
.
Modern versions of the ping-pong lemma can be found in many books such as Lyndon&Schupp, de la Harpe, Bridson&Haefliger and others.
on a set X. Let a1,...,ak be elements of G, where k ≥ 2. Suppose there exist disjoint nonempty subsets
of X with the following properties:
Then the subgroup H = <a1, ..., ak> ≤ G generated
by a1, ..., ak is free
with free basis {a1, ..., ak}.
The argument for the general case is similar to the one given below but requires more careful analysis.
Choose a point x in X such that
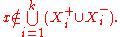
To show that H is free
with free basis a1,...,ak it suffices to prove that every nontrivial freely reduced word in the alphabet
represents a nontrivial element of G.
Let w be such a freely reduced word, that is, w = bnbn−1...b1, where n ≥ 1, where each bj belongs to A and where w does not contain subwords of the form aiai−1 or ai−1ai.
Induction on j shows that for every j = 1, ..., n we have

Thus
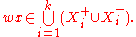
Therefore wx ≠ x and hence w ≠ 1 in G, as required.
The name "ping-pong lemma" is motivated by the fact that, in the above argument, the point bjbj−1...b1x bounces like a ping-pong between the sets X1+, ..., Xk+, X1–,...,Xk– as j varies over j = 1, ..., n.
s of a group acting on a set generate a free product
.
s of G such that |H1| ≥ 3 and |H2| ≥ 2. Suppose there exist two non-empty subsets X1 and X2 of X such that the following hold:
Then the subgroup H=<H1, H2>≤G of G generated by H1 and H2 is equal to the free product
of H1 and H2:
Let G be a group acting on a set X and let H1, H2,...., Hk be nontrivial subgroups of G where k≥2, such that at least one of these subgroups has order
greater than 2.
Suppose there exist disjoint nonempty subsets X1, X2,....,Xk of X such that the following holds:
Then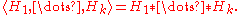
Special linear group
One can use the ping-pong lemma to prove that the subgroup H = <A,B>≤SL(2,Z), generated by the matrices
 and
and 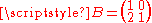
is free
of rank two.
subgroup
s of SL(2,Z) generated by A and B accordingly. It is not hard to check that A and B are elements of infinite order in SL(2,Z) and that

and
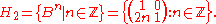
Consider the standard action of SL(2,Z) on R2 by linear transformation
s. Put
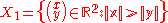
and
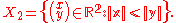
It is not hard to check, using the above explicitly descriptions of H1 and H2 that for every nontrivial g ∈ H1 we have g(X2) ⊆ X1 and that for every nontrivial g ∈ H2 we have g(X1) ⊆ X2. Using the alternative form of the ping-pong lemma, for two subgroups, given above, we conclude that H = H1∗H2. Since the groups H1 and H2 are infinite cyclic, it follows that H is a free group
of rank two.
. Let g, h ∈ G be two non-commuting elements, that is such that gh ≠ hg. Then there exists M≥1 such that for any integers n ≥ M, m ≥ M the subgroup H = <gn, hm> ≤ G is free
of rank two.
on its hyperbolic boundary ∂G by homeomorphism
s. It is known that if a ∈ G is a nontrivial element then a has exactly two distinct fixed points, a∞ and a−∞ in ∂G and that a∞ is an attracting fixed point while a−∞ is a repelling fixed point
.
Since g and h do not commute, the basic facts about word-hyperbolic groups imply that g∞, g−∞, h∞ and h−∞ are four distinct points in ∂G. Take disjoint neighborhoods
U+, U–, V+ and V– of g∞, g−∞, h∞ and h−∞ in ∂G respectively.
Then the attracting/repelling properties of the fixed points of g and h imply that there exists M ≥ 1 such that for any integers n ≥ M, m ≥ M we have:
The ping-pong lemma now implies that H = <gn, hm> ≤ G is free
of rank two.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the ping-pong lemma, or table-tennis lemma, is any of several mathematical statements that ensure that several elements in a group acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set freely generate
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
a free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of that group.
History
The ping-pong argument goes back to late 19th century and is commonly attributed to Felix KleinFelix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
who used it to study subgroups of Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s, that is, of discrete groups of isometries of the hyperbolic 3-space or, equivalently Möbius transformations of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. The ping-pong lemma was a key tool used by Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
in his 1972 paper containing the proof of a famous result now known as the Tits alternative
Tits alternative
In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about the structure of finitely generated linear groups. It states that every such group is either virtually solvable In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about...
. The result states that a finitely generated linear group is either virtually
Virtually
In mathematics, especially in the area of abstract algebra which studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index...
solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
or contains a free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of rank two. The ping-pong lemma and its variations are widely used in geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.
Modern versions of the ping-pong lemma can be found in many books such as Lyndon&Schupp, de la Harpe, Bridson&Haefliger and others.
Formal statement
Let G be a group actingGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set X. Let a1,...,ak be elements of G, where k ≥ 2. Suppose there exist disjoint nonempty subsets
- X1+,...,Xk+ and X1–,...,Xk–
of X with the following properties:
- ai(X − Xi–) ⊆ Xi+ for i = 1, ..., k;
- ai−1(X − Xi+) ⊆ Xi– for i = 1, ..., k.
Then the subgroup H = <a1, ..., ak> ≤ G generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by a1, ..., ak is free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis {a1, ..., ak}.
Proof
To simplify the argument, we will prove the statement under the following mild additional assumption:The argument for the general case is similar to the one given below but requires more careful analysis.
Choose a point x in X such that
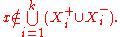
To show that H is free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis a1,...,ak it suffices to prove that every nontrivial freely reduced word in the alphabet
- A = {a1, ..., ak, a1−1, ..., ak−1}
represents a nontrivial element of G.
Let w be such a freely reduced word, that is, w = bnbn−1...b1, where n ≥ 1, where each bj belongs to A and where w does not contain subwords of the form aiai−1 or ai−1ai.
Induction on j shows that for every j = 1, ..., n we have

Thus
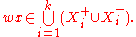
Therefore wx ≠ x and hence w ≠ 1 in G, as required.
The name "ping-pong lemma" is motivated by the fact that, in the above argument, the point bjbj−1...b1x bounces like a ping-pong between the sets X1+, ..., Xk+, X1–,...,Xk– as j varies over j = 1, ..., n.
Ping-pong lemma for several subgroups
There is also a version of the ping-pong lemma which ensures that several subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of a group acting on a set generate a free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
.
A version for two subgroups
Let G be a group acting on a set X and let H1, H2 be two subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of G such that |H1| ≥ 3 and |H2| ≥ 2. Suppose there exist two non-empty subsets X1 and X2 of X such that the following hold:
- X2 is not contained in X1;
- for every h1 ∈ H1, h1 ≠ 1 we have h1(X2) ⊆ X1;
- for every h2 ∈ H2, h2 ≠ 1 we have h2(X1) ⊆ X2.
Then the subgroup H=<H1, H2>≤G of G generated by H1 and H2 is equal to the free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of H1 and H2:
- H = H1∗H2.
A version for an arbitrary finite number of subgroups
The following version of the ping-pong lemma for several subgroups appears in .Let G be a group acting on a set X and let H1, H2,...., Hk be nontrivial subgroups of G where k≥2, such that at least one of these subgroups has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
greater than 2.
Suppose there exist disjoint nonempty subsets X1, X2,....,Xk of X such that the following holds:
- For any i≠j and for any h∈Hi, h≠1 we have h(Xj)⊆Xi.
Then
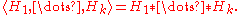
Special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
example
One can use the ping-pong lemma to prove that the subgroup H = <A,B>≤SL(2,Z), generated by the matrices and
and 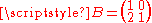
is free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank two.
Proof
Indeed, let H1 = <A> and H2 = <B> be cyclicCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of SL(2,Z) generated by A and B accordingly. It is not hard to check that A and B are elements of infinite order in SL(2,Z) and that

and
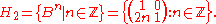
Consider the standard action of SL(2,Z) on R2 by linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s. Put
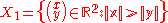
and
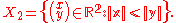
It is not hard to check, using the above explicitly descriptions of H1 and H2 that for every nontrivial g ∈ H1 we have g(X2) ⊆ X1 and that for every nontrivial g ∈ H2 we have g(X1) ⊆ X2. Using the alternative form of the ping-pong lemma, for two subgroups, given above, we conclude that H = H1∗H2. Since the groups H1 and H2 are infinite cyclic, it follows that H is a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank two.
Word-hyperbolic group example
Let G be a word-hyperbolic group which is torsion-free, that is, with no nontrivial elements of finite orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. Let g, h ∈ G be two non-commuting elements, that is such that gh ≠ hg. Then there exists M≥1 such that for any integers n ≥ M, m ≥ M the subgroup H = <gn, hm> ≤ G is free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank two.
Sketch of the proof
The group G actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on its hyperbolic boundary ∂G by homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s. It is known that if a ∈ G is a nontrivial element then a has exactly two distinct fixed points, a∞ and a−∞ in ∂G and that a∞ is an attracting fixed point while a−∞ is a repelling fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
Since g and h do not commute, the basic facts about word-hyperbolic groups imply that g∞, g−∞, h∞ and h−∞ are four distinct points in ∂G. Take disjoint neighborhoods
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U+, U–, V+ and V– of g∞, g−∞, h∞ and h−∞ in ∂G respectively.
Then the attracting/repelling properties of the fixed points of g and h imply that there exists M ≥ 1 such that for any integers n ≥ M, m ≥ M we have:
- gn(∂G – U–) ⊆ U+
- g−n(∂G – U+) ⊆ U–
- hm(∂G – V–) ⊆ V+
- h−m(∂G – V+) ⊆ V–
The ping-pong lemma now implies that H = <gn, hm> ≤ G is free
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank two.
Applications of the ping-pong lemma
- The ping-pong lemma is used in Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s to study their so-called Schottky subgroupsSchottky groupIn mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...
. In the Kleinian groups context the ping-pong lemma can be used to show that a particular group of isometries of the hyperbolic 3-space is not just freeFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
but also properly discontinuousProperly discontinuousIn topology and related branches of mathematics, an action of a group G on a topological space X is called proper if the map from G×X to X×X taking to is proper, and is called properly discontinuous if in addition G is discrete...
and geometrically finite. - Similar Schottki-type arguments are widely used in geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, particularly for subgroups of word-hyperbolic groups and for automorphism groups of trees. - Ping-pong lemma is also used for studying Schottki-type subgroups of mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
s of Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, where the set on which the mapping class group acts is the Thurston boundary of the Teichmüller spaceTeichmüller spaceIn mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
. A similar argument is also utilized in the study of subgroups of the outer automorphism groupOuter automorphism groupIn mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
. - One of the most famous applications of the ping-pong lemma is in the proof of Jacques TitsJacques TitsJacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
of the so-called Tits alternativeTits alternativeIn mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about the structure of finitely generated linear groups. It states that every such group is either virtually solvable In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about...
for linear groups. (see also for an overview of Tits' proof and an explanation of the ideas involved, including the use of the ping-pong lemma). - There are generalizations of the ping-pong lemma that produce not just free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s but also amalgamated free products and HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s. These generalizations are used, in particular, in the proof of Maskit's Combination Theorem for Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s. - There are also versions of the ping-pong lemma which guarantee that several elements in a group generate a free semigroupFree semigroupIn abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
. Such versions are available both in the general context of a group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set, and for specific types of actions, e.g. in the context of linear groups, groups acting on trees and others.
See also
- Free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
- Free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
- Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
- Tits alternativeTits alternativeIn mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about the structure of finitely generated linear groups. It states that every such group is either virtually solvable In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about...
- Word-hyperbolic group
- Schottky groupSchottky groupIn mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...