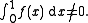In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the notions of prevalence and shyness are notions of "almost everywhere

Almost everywhere

In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

" and "measure zero" that are well-suited to the study of infinite-dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al spaces and make use of the translation-invariant Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

 on finite-dimensional real spaces. The term "shy" was suggested by the American

United States

The United States of America is a federal constitutional republic comprising fifty states and a federal district...

 mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 John Milnor

John Milnor

John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...

.

Prevalence and shyness

Let V be a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

 and let S be a Borel-measurable subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of V. S is said to be prevalent if there exists a finite-dimensional subspace P of V, called the probe set, such that v + p ∈ S for all v ∈ V and λ_P-almost all

Almost all

In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....

 p ∈ P, where λ_P denotes the dim(P)-dimensional Lebesgue measure on P. Put another way, for every v ∈ V, Lebesgue-almost every point of the hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 v + P lies in S.

A non-Borel subset of V is said to be prevalent if it contains a prevalent Borel subset.

A Borel subset of V is said to be shy if its complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

 is prevalent; a non-Borel subset of V is said to be shy if it is contained within a shy Borel subset.

An alternative, and slightly more general, definition is to define a set S to be shy if there exists a transverse measure

Transverse measure

In mathematics, a measure on a real vector space is said to be transverse to a given set if it assigns measure zero to every translate of that set, while assigning finite and positive measure to some compact set.-Definition:...

 for S (other than the trivial measure

Trivial measure

In mathematics, specifically in measure theory, the trivial measure on any measurable space is the measure μ which assigns zero measure to every measurable set: μ = 0 for all A in Σ.-Properties of the trivial measure:...

).

Local prevalence and shyness

A subset S of V is said to be locally shy if every point v ∈ V has a neighbourhood N_v whose intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

 with S is a shy set. S is said to be locally prevalent if its complement is locally shy.

Theorems involving prevalence and shyness

• If S is shy, then so is every subset of S and every translate of S.

• Every shy Borel set S admits a transverse measure that is finite and has compact
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
   support
  Support (measure theory)
  In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
  
  . Furthermore, this measure can be chosen so that its support has arbitrarily small diameter
  Diameter
  In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
  
  .

• Any finite or countable union
  Union (set theory)
  In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
  
   of shy sets is also shy.

• Any shy set is also locally shy. If V is a separable space, then every locally shy subset of V is also shy.

• A subset S of n-dimensional Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
   Rⁿ is shy if and only if
  If and only if
  In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
  
   it has Lebesgue measure zero.

• Any prevalent subset S of V is dense in V.

• If V is infinite-dimensional, then every compact subset of V is shy.

In the following, "almost every" is taken to mean that the stated property holds of a prevalent subset of the space in question.

• Almost every continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
   from the interval
  Interval (mathematics)
  In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
  
   [0, 1] into the real line
  Real line
  In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
  
   R is nowhere differentiable; here the space V is C([0, 1]; R) with the topology induced by the supremum norm.

• Almost every function f in the L^p space
  Lp space
  In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
  
   L¹([0, 1]; R) has the property that

Clearly, the same property holds for the spaces of k-times differentiable function

Differentiable function

In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...

s C^k([0, 1]; R).

• For 1 < p ≤ +∞, almost every sequence a = (a_n)_n∈N in ℓ^p has the property that the series

diverges.

• Prevalence version of the Whitney embedding theorem: Let M be a compact manifold
  Manifold
  In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
  
   of class C¹ and dimension d contained in Rⁿ. For 1 ≤ k ≤ +∞, almost every C^k function f : Rⁿ → R^2d+1 is an embedding
  Embedding
  In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
  
   of M.

• If A is a compact subset of Rⁿ with Hausdorff dimension
  Hausdorff dimension
  thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
  
   d, m ≥ d, and 1 ≤ k ≤ +∞, then, for almost every C^k function f : Rⁿ → R^m, f(A) also has Hausdorff dimension d.

• For 1 ≤ k ≤ +∞, almost every C^k function f : Rⁿ → Rⁿ has the property that all of its periodic point
  Periodic point
  In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
  
  s are hyperbolic. In particular, the same is true for all the period p points, for any integer p.